-- In regard to this rule why did we earlier introduce the notion of the union of two sets?An experiment is any procedure that can be replicated but which can result in different outcomes. The outcome cannot be predicted with certainty ex ante.
A random variable is a rule or function that assigns a number to the outcome of an experiment.
A discrete random variable is one that takes countably distinct values. The number of distinct values need not be finite.
A probability density function is a rule that assigns a numerical likelihood of occurrence to a discrete random variable.
A cumulative density function assigns a numerical likelihood to a closed and compact set of possible occurrences of a random variable.
A continuous random variable is a rule that assigns a numerical value to the outcome of an experiment. For example, the experiment might be weighing cans of ground coffee as they come off the production line. The reported weight of a can can be measured to any degree of accuracy so the random variable 'weight of can' can take on any real number. This causes us to reconsider the notions of probability density function and cumulative density function.
Can two events be both independent and mutually exclusive?
Union and Intersection
a. The probability of an event must be between 0 and 1.
b. The sum of the probabilities of a set of collectively exhaustive and mutually exclusive events must be 1.
c. Countable additivity: The probability of the union of disjoint events is equal to the sum of the probabilities of the individual events.
a. The Addition Rule -- In regard to this rule why did we earlier introduce the notion of the union of two sets?
b. The Multiplication Rule 
-- In regard to this rule why did we earlier introduce the notion of the intersection of two sets?
c. Probability and Two Way Tables
X |
||||
x1 |
x2 | |||
Y |
y1 | .2 | .1 | .3 |
| y2 | .3 | .4 | .7 | |
| .5 | .5 | 1.0 | ||
d. Conditional Probability 
e. Can you use the table to illustrate independence, collectively exhaustive, and mutually exclusive?
Central Tendency Mean, median, mode
Dispersion Variance, standard deviation, range, quantiles
Expected value of a random variable is the probability weighted average of its collectively exhaustive and mutually exclusive outcomes. Your GPA is a weighted average. The simplest example of the expected value of a random variable is the mean,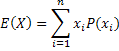 
. This idea is generalizable to functions of random variables, 
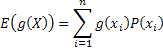, so the variance of a random variable is an expectation.
Properties of Expected Value
a. The expected value of a constant is the constant.
b. The expected value of a constant times a random variable is the constant times the expected value of the random variable.
c. The expected value of a linear combination of random variables is the sum of the expected values.
d. The fact that the variance is an expectation leads to the following properties
1. The variance of a constant is zero.
2. The variance of a random variable defined as Z = a +/- bY is Var(Z) = b2Var(Y)
Standardizing or normalizing a random variable 
. Mean = ?, variance = ?
Covariance 
1. Independence implies Cov(X,Y) = 0.
2. 
Correlation is a way of standardizing the covariance so that we can make comparisons. The correlation coefficient is always between -1 and +1.
Variance of the sum of random variables uses the preceding rules and definitions: 
Two random variables, X and Y, are thought/known to have some association. Previously we were interested in, say, the expected value of Y regardless of the value(s) taken on by X. That is, we know how to find the expected value of the marginal distribution of Y. Suppose we are really interested in the mean of Y for a particular realization of X.
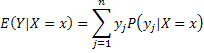
Properties of Conditional Expectation
1. If you take the Expectation of a function of the variable upon which you have conditioned, say X=x, then you get back the function evaluated at the value X=x.
2. Property 1 also holds for linear combinations involving the conditioned upon variable.
3. If X and Y are independent then E(Y|X) = E(Y)
4. Iterated Expectations 
The Normal Distribution - Any linear combination of normal random variables is itself normally distributed.
The Chi-square Distribution - The chi-square is constructed as the sum of squared normal random variables. The number of degrees of freedom for the so constructed chi-square is equal to the number of independent normal rv's in the sum.
Student's t Distribution is the ratio of a N(0,1) to the square root of a chi-square divided by (scaled by) its degrees of freedom.
The F Distribution is the ratio of two chi-square rv's divided by their respective degrees of freedom.