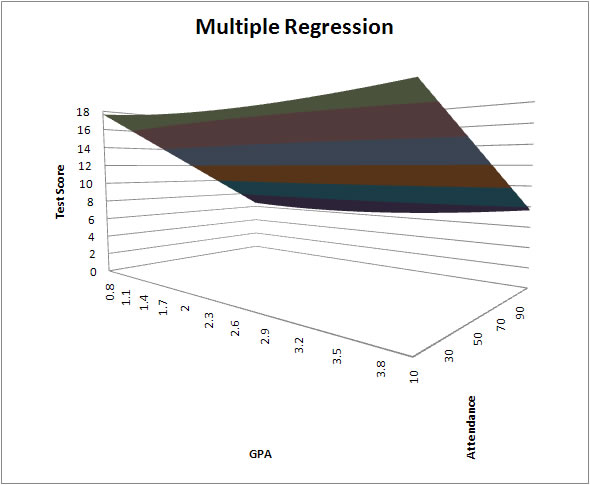
Simple regression is just a line or curve in a plane. Multiple regression gives us the opportunity to produce a surface in a multi-dimensional space. Having more than one explanatory variable allows us to explore all the richness of the phenomenon that interests us. When there are two regressors we might get something like

![]()
1. The coefficient ![]() is the marginal or partial effect of x2 on y, all other variables held constant. By marginal effect we mean that a one unit increase in x2 causes y to increase by the amount
is the marginal or partial effect of x2 on y, all other variables held constant. By marginal effect we mean that a one unit increase in x2 causes y to increase by the amount ![]() . The coefficient
. The coefficient ![]() is also the partial derivative of y with respect to x2. This is generalizable to many right hand side variables.
is also the partial derivative of y with respect to x2. This is generalizable to many right hand side variables.
2. There is also an analogy to the total differential of calculus. Namely, ![]() in which we change all of the explanatory variables simultaneously.
in which we change all of the explanatory variables simultaneously.
3. A bit of algebra can be used to show that there is a correspondence between the regression coefficients and the partial correlation between xi and y. By partial correlation we mean that we use all the RHS variables except xi to explain y and then go on to see if there is any variation in y that is left over for xi to explain.
There are two approaches which turn out to be equivalent.
1. We could use our principal of analogy as we did for simple regression. For example,
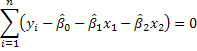
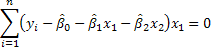
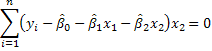
These three equations could be solved for the three unknowns.
2. The second approach is to pick our guesses as to minimize the sum of squared differences between the observed values of y and our best guesses expressed as
![]() .
.
2.a. If we are willing to assume that the specified model is correct then we can interpret the OLS estimator as a minimum distance estimator since the sum of squares is a distance measure.
2.b. The sum of squared errors is a quadratic form in the unknowns, therefore it will have a unique minimum that can be found by setting the first derivatives to zero and solving the resulting system for the unknowns. The objective function is
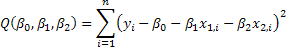
![]()
![]()
![]()
Upon doing the derivatives we would find that the first order conditions are nothing other than the equations that we wrote down for the analogy approach.
All the sums of squares retain their previous definitions.
Similarly, R2 is still SSE/SST or 1 - SSR/SST.
1. The model ![]() is presumed to be correctly specified.
is presumed to be correctly specified.
2. We have a random sample of data for each of the random variables.
3. None of the independent variables is constant.
4. The independent variables are linearly independent of one another. The indepedent variables are said to be NOT collinear. Notice that in the same sentence we have used "independent" in two different ways.
5. As in the previous chapter the expected value of the error conditional on any of the independent variables is zero.
If an irrelevant variable is included in a model specification then logic tells us that the coefficient on that variable should be zero in the population regression function, and in any sample regression the estimate should be close to zero. Of course, in any given sample the coefficient on the irrelevant variable my not be close to zero either numerically or statistically.
The ommission of a relevant variable is a problem.
The correct model is ![]()
but we mistakenly estimate the parameters of ![]()
In the mistaken model the slope estimator is given by
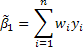
Now subsitute away from y by the correct model.
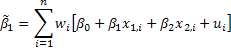
From the properties of the weights wi we can write
![]()
The middle term is ![]() times the result of regressing x2 on x1 and the third term is zero in expectation. The direction of the bias depends on the sign of
times the result of regressing x2 on x1 and the third term is zero in expectation. The direction of the bias depends on the sign of ![]() and the sign of the correlation between x1 and x2. If x1 and x2 are uncorrelated then, in the parlance of mathematics, they are orthogonal to one another and there is no bias.
and the sign of the correlation between x1 and x2. If x1 and x2 are uncorrelated then, in the parlance of mathematics, they are orthogonal to one another and there is no bias.
The sample correlation between x1 and x2 rears its ugly head when we consider the sampling variances of the slope estimators. This is important because we use the variances of the slope estimators in the denominator in the construction of the t-statistics for tests of hypothesis. If x1 and x2 are correlated then it could cause us to either under- or over-state the t-statistics.
Some definitions:
![]() is the coefficient of determination for the regression of xj on all of the other independent variables.
is the coefficient of determination for the regression of xj on all of the other independent variables.
![]() is the total sum of squares for xj in the sample.
is the total sum of squares for xj in the sample.
With some tedious algebra
![]()
What do we conclude?
![]()
A great big caveat is that under the assumptions of the previous chapter, multicollinearity is a problem in the particular sample. The only real solution is to get either more data or new data.