Temple University

Department of Economics

Economics 615

Heteroscedasticity and Autocorrelation

 

1. In his pioneering study of the demand for electricity ("Some Calculations of Electricity Consumption in Great Britain", Journal of the Royal Statistical Society (A), no. 114, part III, pp. 351-371) H. Houthakker collected data for 42 towns in the U.K. for 1937-1938. The data is in the file ukelec.txt. The variables are
CUST - # of customers in thousands in the town
INC - average income of customers in the town (pounds sterling/year)
MC4 - marginal cost of electricity in 1933-34
MC6 - marginal cost of electricity in 1935-36
MC8 - marginal cost of electricity in 1937-38 (all 3 MC's are pence/KWH)
GAS6 - marginal price of gas in 1935-36
GAS8 - marginal price of gas in 1937-38 (both GAS are in pence/therm)
KWH - per capita electricity consumption in the town
CAP - a measure of electrical appliance consumption capacity in KW
EXPEN - average total expenditure on electricity (pounds sterling)

(Note: 1 pound = 20 shillings and 1 shilling = 12 pence)

As a first step you will need to create the new variable PRecip=1/MC6.
Consider the electricity demand model

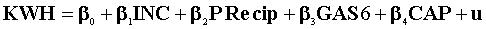
  1. Using the data from ukelec.txt, construct the OLS estimates of the parameters of this model. Comment on the t-statistics.
  2. Construct White's heteroscedasticity robust standard errors. How do they compare with those reported in part a.?
  3. Do two different tests for heteroscedasticity. The first one is to be a Goldfeld Quandt test using the first 18 and the last 18 observations. The second is to be White's general test.
  4. Correct for heteroscedasticity. (Hint: This problem is not unlike the test scores problem in the lecture notes.)
  5. From your heteroscedasticity corrected results compute the income, own and cross price elasticities of demand at the observation corresponding to the median consumption of electricity. Are your estimates plausible?

2. Monetary theory suggests that the demand for money (M) depends on a scale variable such as GDP, and an opportunity cost of holding money such as the interest rate (INT).  Read data from the file BRD.txt. The four variables in the file are Money, GNP, Price Index, and Interest Rate. The observations are for the period 1972Q1 -- 1989Q4.

a. Deflate money and GDP by the Price index in BRD.txt. Create the opportunity cost of holding money as R=1+(INT/100). Take the natural log of real Money, real GDP and the opportunity cost of holding money.
  1. Estimate the parameters of

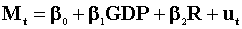
    2. by OLS using the real, logged data, of course.

  2. Use the Durbin Watson test for first order serial correlation.
  3. Use the LM test for higher orders of serial correlation.
  4. Decide on an appropriate degree of serial correlation and correct for it.
  5. Using the residuals from the OLS regression of part a., estimate the parameters of . One can use 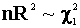as a test statistic for the hypothesis that 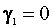.  Report your results from the regression and construct the test statistic. For large values of the test statistic one rejects the null. This is known as a test for first order autoregressive conditional heteroscedasticity. In this example, what do you conclude about fist order ARCH?