Temple University
Department of Economics
Economics 615
Econometrics I
Midterm Exam
Directions: This is a closed book exam. You may have 2 1/2 hours to complete the exam. You must answer all questions. The point values are shown. Your answers must be your own work.
X |
||||||
0 |
1 |
2 |
3 |
|||
Y |
1 |
1/8 |
0 |
0 |
1/8 |
1/4 |
2 |
0 |
1/4 |
1/4 |
0 |
1/2 |
|
3 |
0 |
1/8 |
1/8 |
0 |
1/4 |
|
1/8 |
3/8 |
3/8 |
1/8 |
1 |
||
2. (20 points) For the probability density
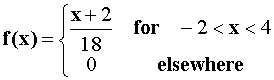
3. (10 points) If x has a normal distribution with mean 3 and variance 16, what are the following:
4. (30 points) For the sample data 12, 15, 9, 3, 23, 1, 5, 8, 11, 17 drawn from a
normal distribution with mean ![]() and variance
and variance![]() .
.
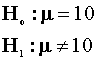
at the 95% level using the classical framework.
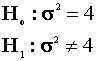
at the 95% level using the classical framework.
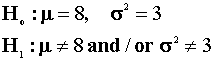
at the 95% level.
5. (15 points) Suppose that in a sample of 100 observations from a normal distribution
with mean ![]() and variance
and variance ![]() you are told that 25% of the observations are
less than 2.5 and 55% are less than 5.3. Estimate
you are told that 25% of the observations are
less than 2.5 and 55% are less than 5.3. Estimate ![]() and
and ![]() .
.