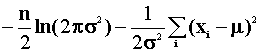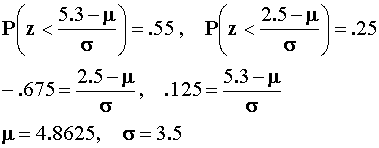Temple University
Department of Economics
Economics 615
Econometrics I
Midterm Exam
Directions: This is a closed book exam. You may have 2 1/2 hours to complete the
exam. You must answer all questions. The point values are shown. Your answers must be your
own work.
- (25 points) Use the following joint distribution
| |
X |
|
0 |
1 |
2 |
3 |
|
Y |
1 |
1/8 |
0 |
0 |
1/8 |
1/4 |
2 |
0 |
1/4 |
1/4 |
0 |
1/2 |
3 |
0 |
1/8 |
1/8 |
0 |
1/4 |
| |
|
1/8 |
3/8 |
3/8 |
1/8 |
1 |
- What is E(X)?
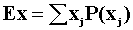
Ex=1/8(0)+3/8(1)+3/8(2)+1/8(3)=1.5
- What is E(Y)?
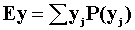
Ey=1(1/4)+2(1/2)+3(1/4)=2
- What is E(X|Y=2)?
| x |
P(x|y=2) |
xP(x|y=2) |
| 0 |
0 |
0 |
| 1 |
1/2 |
1/2 |
| 2 |
1/2 |
1 |
| 3 |
0 |
0 |
E(x|y=2)=1.5
- What is E(X|Y=1)?
| x |
P(x|y=1) |
xP(x|y=1) |
| 0 |
1/2 |
0 |
| 1 |
0 |
0 |
| 2 |
0 |
0 |
| 3 |
1/2 |
1.5 |
E(x|y=1)=1.5
- What is E(XY)?
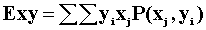
x, y |
xy |
P(x,y) |
xyP(x,y) |
0,1 |
0 |
1/8 |
0 |
1,1 |
1 |
0 |
0 |
2,1 |
2 |
0 |
0 |
3,1 |
3 |
1/8 |
3/8 |
0,2 |
0 |
0 |
0 |
1,2 |
2 |
1/4 |
4/8 |
2,2 |
4 |
1/4 |
1 |
3,2 |
6 |
0 |
0 |
0,3 |
0 |
0 |
0 |
1,3 |
3 |
1/8 |
3/8 |
2,3 |
6 |
1/8 |
6/8 |
3,3 |
9 |
0 |
0 |
Exy=3
- What is the covariance of X and Y?
Cov(x,y)=Exy-ExEy=3-1.5(2)=0
- Are X and Y independent? How do you know? How do you reconcile your answers in a., c.,
d., and f.?
x and y are not independent. We conclude this from the fact that the intersection is
not equal to the product of the marginals. We cannot rely on the conditional expectation
or the covariance to make this inference since these are necessary conditions, but not
sufficient.
2. (20 points) For the probability density
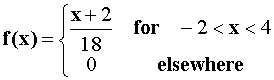
- Is this a bona fide density? How do you know?
Yes, it is a bona fide density. For all intervals 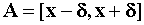 we can show 0<P(A)<1 and the integral over the domain is
one.
we can show 0<P(A)<1 and the integral over the domain is
one.
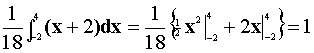
- Find E(X).
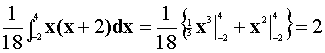
- Find Variance(X).
Var(x)=Ex2-(Ex)2
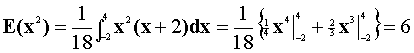
Var(x)=6-22=2
3. (10 points) If x has a normal distribution with mean 3 and variance 16, what are
the following:
- Prob[ |x| > 7 ] ?
P(|x|>7)=P(x<-7)+P(x>7)
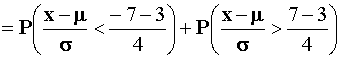
=P(z<-2.5)+P(z>1)=.1649
Prob[ x > -2 | x<4 ] ?
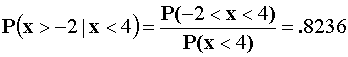
4. (30 points) For the sample data 12, 15, 9, 3, 23, 1, 5, 8, 11, 17 drawn from a
normal distribution with mean 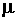 and variance
and variance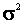 .
.
- Compute the sample mean.
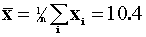
Compute the sample standard deviation.
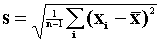
xi |
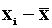
|
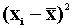
|
12 |
1.6 |
2.56 |
15 |
4.6 |
21.16 |
9 |
-1.4 |
1.96 |
3 |
-7.4 |
54.76 |
23 |
12.6 |
158.76 |
1 |
-9.4 |
88.36 |
5 |
-5.4 |
29.16 |
8 |
-2.4 |
5.76 |
11 |
.6 |
.36 |
17 |
6.6 |
43.56 |
s2=45.155 s=6.7197
Test the hypothesis
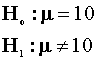
at the 95% level using the classical framework.
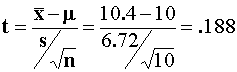
The critical values are -2.262 and 2.262. Therefore do not reject
the null.
Test the hypothesis
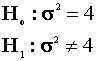
at the 95% level using the classical framework.
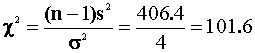
The critical value is 16.91, so reject the null.
Using a likelihood ratio test, test the following hypothesis:
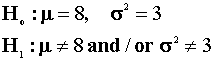
at the 95% level.
The density is 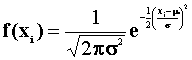 , so the log likelihood
is
, so the log likelihood
is
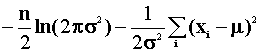
In the restricted parameter space (under the null hypothesis) make the substitution 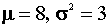 . The log likelihood is -92.015.
. The log likelihood is -92.015.
In the unrestricted parameter space (under the alternate hypothesis) make the
substitution 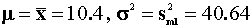 . The log likelihood
evaluated at the sample data is -32.21.
. The log likelihood
evaluated at the sample data is -32.21.
The test statistic is -2(-92.05-(-32.21))=119. For any reasonable level of test and two
degrees of freedom we reject the null.
5. (15 points) Suppose that in a sample of 100 observations from a normal
distribution with mean 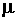 and variance
and variance 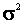 you are told that 25% of the observations are
less than 2.5 and 55% are less than 5.3. Estimate
you are told that 25% of the observations are
less than 2.5 and 55% are less than 5.3. Estimate 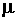 and
and 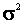 .
.
P(x<5.3)=.55, P(x<2.5)=.25
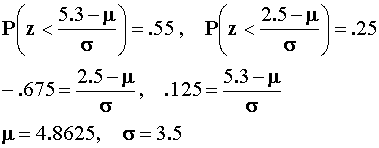
![]()
![]()
![]()
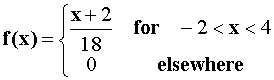
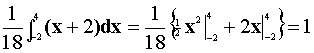
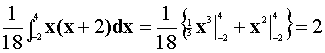
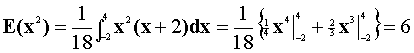
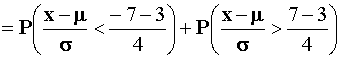
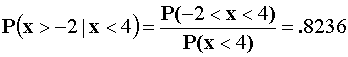
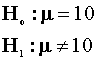
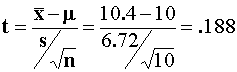
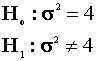
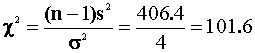
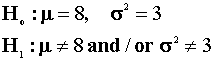
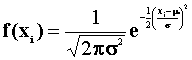 , so the log likelihood
is
, so the log likelihood
is