Temple University
Department of Economcs
Economics 8009
1. The table gives daily sales of cars by a local dealership, from a 0 minimum to a 6 maximum, and the number of days for which that number of sales happened during a 100-day survey. That is, 0 cars were sold on 6 days, 1 car on 8 days, etc.
Cars per Day |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Number of days |
6 |
8 |
22 |
20 |
15 |
16 |
13 |
(a) Enter the probability density in the following table:
Car Sales per Day, X |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
f(x) |
6/100 |
8/100 |
22/100 |
20/100 |
15/100 |
16/100 |
13/100 |
(b) Compute the expected value of X and give its meaning.
(6/100)(0)+(8/100)(1)+(22/100)(2)+(20/100)(3)+60/100+80/100+78/100 = 3.30
(c) Compute the variance and standard deviation of X.
| Prob | x | x-mean(x) | (x-mean(x))2 | (x-mean(x))2 Prob |
| 0.06 | 0 | -3.3 | 10.89 | 0.6534 |
| 0.08 | 1 | -2.3 | 5.29 | 0.4232 |
| 0.22 | 2 | -1.3 | 1.69 | 0.3718 |
| 0.20 | 3 | -.3 | 0.09 | 0.018 |
| 0.15 | 4 | 0.7 | 0.49 | .0735 |
| 0.16 | 5 | 1.7 | 5.763 | 0.462 |
| 0.13 | 6 | 2.7 | 7.29 | .9477 |
Var(x) = 2.95
Std Dev(x) = 1.718
2. The following table gives data on 100 observations on 3 mutual funds, Y, with the average rates of return, X, of -6%, 5%, and 10%.
Y |
||||
1 |
2 |
3 |
||
X |
-6 |
0 |
10 |
15 |
5 |
10 |
15 |
20 |
|
10 |
25 |
5 |
0 |
|
(a) Find the marginal probability functions of X and Y. Enter your answer in the table below.
Y |
|||||
1 |
2 |
3 |
|||
X |
-6 |
0 |
.1 |
.15 |
0.25 |
5 |
.1 |
.15 |
.20 |
0.45 |
|
10 |
.25 |
.05 |
0 |
.30 |
|
.35 |
.30 |
.35 |
|||
(b) Find the conditional probability density function of X given that Y equals 3.
f(X|Y=3) = {.15/.35, .20/.35} = {3/7, 4/7} ={0.4286, 0.5714}
(c) Find the covariance of X and Y.
Cov(X,Y) = EXY - EXEY
EX = .25(-6)+.45(5)+.3(10) = 3.75
EY = .35(1) + .3(2) + .35(3) = 2
| f(X,Y) | XY | XY*f(X,Y) |
| 0 | -6 | 0 |
| .1 | 5 | .5 |
| .25 | 10 | 2.5 |
| .1 | -12 | -1.2 |
| .15 | 10 | 1.5 |
| .05 | 20 | 1 |
| .15 | -18 | -2.7 |
| .2 | 15 | 3 |
| 0 | 30 | 0 |
From the table EXY = 4.6 So Cov(X,Y) = 4.6 - 7.5 = -2.9
(d) Verify if X and Y are statistically independent.
They are not independent because the intersection is not the product of the marginals. Or, the marginal and the conditional are not equal.
If X and Y are independent, then their covariance is zero. This follows because under independence,
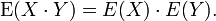
The converse, however, is generally not true: Some pairs of random variables have covariance zero although they are not independent.
In order to understand how the converse of this proposition is not generally true, consider the example where Y = X2, E(X) = 0, and E(X3) = 0. In this case, X and Y are obviously not independently distributed.
3. Let Z be a standard normal variable. Find:
(a) P(Z >- 0.54) = .7054
(b) P(0.35<Z<1.67) = .9525 - .6368 = .3157
4. Suppose a mutual fund has an annual rate of return that is approximately normally distributed with mean 7% and variance 64.
(a) Find the probability that the annual return will be negative.
P(ret<=0) = P(z<=((0-7)/8)) = P(Z<=-.875) = 1-.8092 = .1908
(b) Find the probability that an annual return will exceed 10%.
P(ret>10) = P(z>(10-7)/8) = P(z>.375) = 1 - .6461 = .3538
5. Prove that if A and B are mutually exclusive then 
.
6. Prove that 
is a cdf. Along the
way you will have to state the support of the cdf.
First you need to derive the pdf from the cdf,
6.1. then show that the cdf always lies between 0 and 1.0
6.1.a Use limits to show that as x -> 0 the cdf goes to 0.0 and as x -> infinity the cdf goes to one, as x -> -infinity F < 0 and therefore the support is {0, infinity}.
6.1.b for x in {0, infinity} the slope of F, i.e. its density e-x, is always positive and F" is negative so F is an increasing function on its support
Conclude that 0<=cdf<=1 and
6.2. That the pdf integrates to 1.0
From F(x) we see that F(infinity) = 1 and F(0) = 0 so the pdf integrates to one.