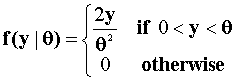Temple University
Department of Economics
Economics 615
Sampling and Estimation
- (HC) Let X1 and X2 be two draws from the distribution having
p.d.f.
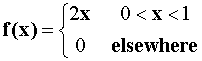
Find 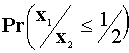 .
.
- (HC) Let X have the p.d.f.
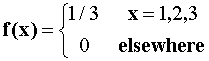 .
.
Find the p.d.f. of the random variable Y=2X+1. (Hint: This is a one to one
transformation of random variables of the discrete type.)
(HC) Let X1, X2 be a random sample of size 2 from the distribution
having p.d.f. 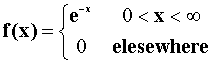 .
.
Let Y1=X1+X2 and Y2=X1/(X1+X2).
Show that Y1 and Y2 are stochastically independent.
(P) Consider the sample values Yt (t=1,2,…,T). Show
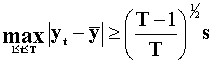
where 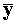 and s denote
the realized values of the sample mean and standard deviation respectively.
and s denote
the realized values of the sample mean and standard deviation respectively.
(P) Consider a random sample Yt (t=1,2,…T) from a 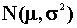 population. Find the minimum value of T such
that the probability is .95 that the sample mean will not differ from the population mean
by more than 25 percent of the standard deviation.
(P) Suppose Y=[y1, Y2,…YT]'
population. Find the minimum value of T such
that the probability is .95 that the sample mean will not differ from the population mean
by more than 25 percent of the standard deviation.
(P) Suppose Y=[y1, Y2,…YT]'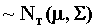 where
where 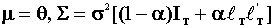 ,
, 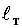 is a Tx1 vector with each element equal to
unity, and
is a Tx1 vector with each element equal to
unity, and 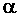 is a scalar such that
is a scalar such that 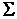 is positive definite.
is positive definite.
- For what value of
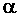 does Y comprise a
random sample?
does Y comprise a
random sample?
- Find Var(
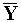 ) and simplify your answer.
) and simplify your answer.
- Is s2 and unbiased estimator of
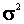 ?
?
- (P) Let Yt (t=1,2,…T) be a random sample from the p.d.f.
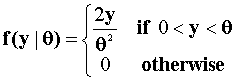
- Show
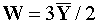 is an unbiased estimator for
is an unbiased estimator for 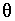 .
.
- Find the Cramer-Rao lower bound.
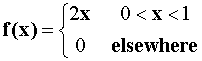
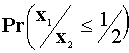 .
.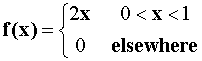
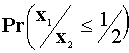 .
.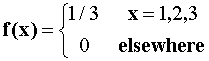 .
.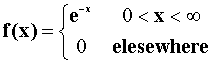 .
.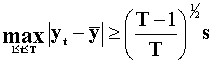
![]() and s denote
the realized values of the sample mean and standard deviation respectively.
and s denote
the realized values of the sample mean and standard deviation respectively.