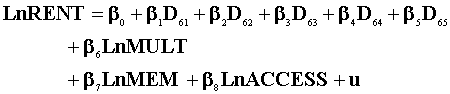Temple University

Department of Economics

Economics 615

Least Squares

A copy of this question set and the data are in a single self-extracting file.

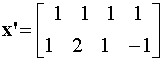  1. Consider the regression model , where Eu=0 and Euu' = I4 , and

    2. .

    Let and where 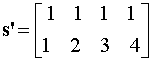. Show that is a better estimator than .

  2. Suppose that the parameters of the model

are to be estimated following set of six observations:

yi

Xi1

Xi2

10

1

0

17

4

6

13

2

4

14

2

3

12

1

1

15

3

5
  1. Are x1 and x2 linearly independent?
  2. What are the least squares estimates of ?
  3. Add 5 to each observation on y and 10 to each observation on x1 and x2 and construct new estimates of . How does your answer compare to that in b.?
  4. Return to the original data. Multiply each observation on y by 10 and recalculate the LS estimates. How does your answer compare to that in b.?
  5. Return to the original data. Multiply each observation on x1 by 10 and compute new LS estimates. How does your answer compare to that in b.?
  6. What do you conclude about the origin and scale in LS applications?

3.  Retrieve the file CHOW.txt (Gregory Chow, Technological Change and the Demand for Computers, American Economic Review, Vol. 57, No. 5, pp. 1117-1130) for this example. The file contains 137 observations on 11 variables. The variable titles are in the first row of the file. Take natural logs of the variables RENT (monthly rental rate of a computer), MULT (time to complete a multiplication instruction), ACCESS (time required to access information from memory), and ADD (time needed to an addition). Take the natural log of MEM=WORDS*BINARY*DIGITS. (WORDS = # of words in main memory, BINARY=# of bits per word, DIGITS=# of equivalent binary digits) There is a variable called YEAR for the year in which the computer was introduced. Use YEAR to construct dummy variables for 1961, 1962, 1963, 1964 and 1965.

  1. Estimate the parameters of the multiple regression
    for the years 1960-1965 (observations 56 to 137).
  2. For the purposes of constructing the dummy variables 1960 was taken to be the base year. If you take anti-logs of the dummy coefficients you will get a quality adjusted price index for the years 1960 through 1965. Do this. Describe the behavior of the index.
  3. Construct a new dummy variable that takes the value of one for the years 1961-1965 and zero otherwise. Regress LnRENT on an intercept, this new dummy, and the explanatory variables LnMULT, LnMEM, and LnACCESS. How do your results differ from part a.?