The problem posits the simple linear regression model

The simple correlation coefficient is

1. Notice that there is no presumption about causation between x and y. This is quite different from the coefficient of determination in a regression model. In a regression model y is always understood to be the dependent variable. The coefficient of determination will depend on the choice of left hand side variable. However, if y is taken to be the dependent variable, then the square of the correlation coefficient and the coefficient of determination will be equal in a simple linear regression model. If you wanted to use this fact in your answers then you need to prove the equality first.

2. When told to prove or demonstrate something you cannot use the result to be proven in the proof!

3. When told to prove or demonstrate something you cannot pull results out of thin air without showing where the result came from or giving attribution.

The Likelihood Ratio Test for Linear Restrictions on the Regression Coefficients

For the maintained model we have

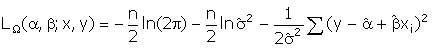
The maximum likelihood estimator of the error variance under the null hypothesis is

Making the substitution, the log likelihood under the null reduces to

For the restricted model, ω, we have by analogy

The likelihood ratio statistic is

Making the substitutions

The maximum likelihood estimator of the intercept is

Making this substitution and doing some rearranging gives

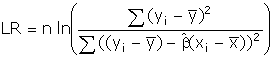
In the next steps you should expand the square in the denominator, then multiply the numerator and denominator by the inverse of the sum of squared deviations of y about its mean. If you do the algebra correctly then you will obtain

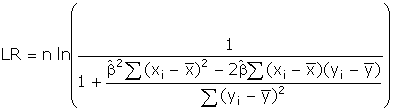
The maximum likelihood estimator for the slope coefficient is

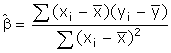
Substitute this expression into the LR

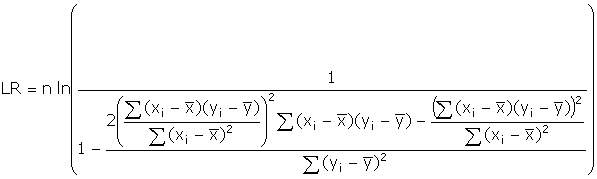
With some rearranging and applying the definition of the correlation coefficient you will get

Which was the desired result.

The Wald Test for Linear Restrictions

We begin by making use of the definition of the Wald test.

The estimate of the variance of the ML estimator for the slope is

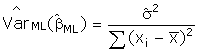
Utilizing some of the steps from the answer to the LR question (substituting in for the estimators for the intercept and slope) we can rewrite the estimate of the error variance in the following way

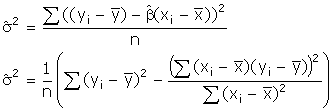
Making the substitution into the Wald statistic

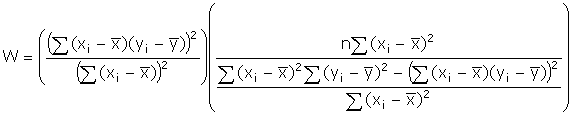
With some cancellations and rearranging you will obtain

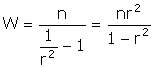
Which was the desired result.

The Lagrange Multiplier Test for Linear Restrictions

Recall the likelihood function from the section on the likelihood ratio test. Differentiate that function with respect to each of the unknown parameters.

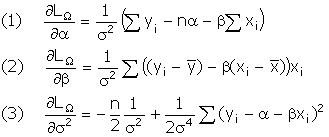
(a) We will also need the inverse of the negative of the information matrix. Recall that the information matrix is the Hessian for the likelihood function. Since (1) and (3) are both zero when evaluated at the restrictions,

,

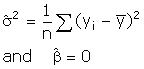we only need one term in the information matrix. Namely, after first substituting the ML estimator for the intercept into (2),

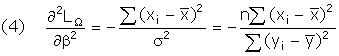
The second equality in (4) comes from evaluating the derivative at the restrictions.

(b) From the observation in (a) and the definition of the LM test in the text we can write

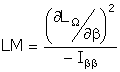
From (2) we can write

Plugging into the test statistic

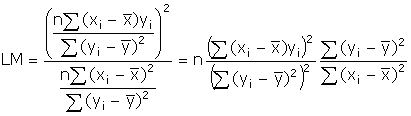
Which is the desired result.