Where 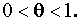 One can use
several different test statistics for the test of hypothesis:
One can use
several different test statistics for the test of hypothesis:
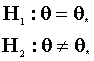
a. Derive the likelihood ratio test statistic.
b. Derive the Wald test statistic.
c. Derive the lagrange multiplier test statistic.
(B) For the period 1947-1971 there are data in the file klem.txt on the quantities for
gross output quantity (QY), capital input (QK), labor input (QL), energy input (QE), and
material input (QM), as well as the corresponding nominal prices. You will also find the
quantity of value added output (QV) and its nominal price.
2.a. Plot the quantities. Plot the nominal prices. What is happening to the series?
2.b. Deflate the input prices by the price of output and plot the resulting series.
Which series are increasing/constant/decreasing? Comment.
2.c. Create the input-output coefficients KY=QK/QY, LY=QL/QY, EY=QE/QY, MY=QM/QY. Plot
these series. Was production becoming more or less labor/capital/energy intensive?
2.d. Verify the accounting relationship between gross output and value added.
2.e. Fit the data to the regression models
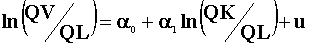
and
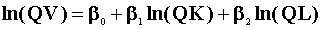
Discuss your results.
2.f. Test the implicit restriction in part 2.e.
Use the data in chow.txt
from Gregory Chow, Technological
Change and the Demand for Computers, American Economic Review, Vol. 57, No. 5, pp.
1117-1130 for this example. The file contains 137 observations on 11 variables. The
variable titles are in the first row of the file. Take natural logs of the variables RENT
(monthly rental rate of a computer), MULT (time to complete a multiplication instruction),
ACCESS (time required to access information from memory), and ADD (time needed to
complete an
addition). Take the natural log of MEM=WORDS*BINARY*DIGITS. (WORDS = # of words in main
memory, BINARY=# of bits per word, DIGITS=# of equivalent binary digits) There is a
variable called YEAR for the year in which the computer was introduced. Use YEAR to
construct dummy variables for 1961, 1962, 1963, 1964 and 1965. The first generation of
computers is dated as 1954 through 1959. The period 1960 - 1965 is the second generation.
Using the variable YEAR, construct a dummy variable for the latter period. The dummy will
be one for the years 1960-1965, and zero otherwise.
A. Fit the model
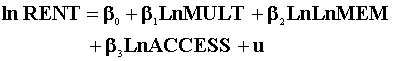 Take the natural log of MEM
only once!
Take the natural log of MEM
only once!
to each period.
B. Fit the same model to all 137 observations.
C. Include the dummy in the model and fit it to all 137 observations.
D. Using the results from A, B and C, construct appropriate tests for the stability of the
intercept and slopes over the two periods. Which specification do you conclude is best?
![]()
![]()
![]() One can use
several different test statistics for the test of hypothesis:
One can use
several different test statistics for the test of hypothesis: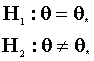
![]()
![]()
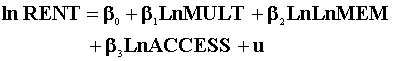 Take the natural log of MEM
only once!
Take the natural log of MEM
only once!