Temple University
Static Games of Incomplete Information: Part II
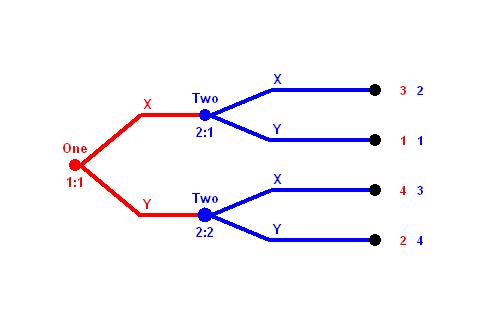
As a starting point consider the following game of imperfect information between two players
| Player 2 | |||
| X | Y | ||
| Player 1 | X | 3,2 | 1, 1 |
| Y | 4,3 | 2, 4 | |
Player 1 has the dominant strategy of playing Y. Eliminating the dominated strategy leads to Player 2 playing Y. The solution to the game is <Y, Y>
Now suppose that Player 1 moves first, and Player 2 moves second knowing what 1 has played; a dynamic game of perfect information.

Using roll back induction the solution to the game is strategy X by Player 1 and then X by player 2, denoted <X, X>. Note that this was not even a Nash Equilibrium in the Normal Form Game! This happens because Player 2 cannot make a credible commitment to always play Y.
Now suppose that Player 1 is known to be a liar. Although Player 1 announces the strategy he intends to play, he might not be telling the truth. Fortunately, Player 2 knows that Player 1 tells the truth 75% of the time. The game tree now becomes
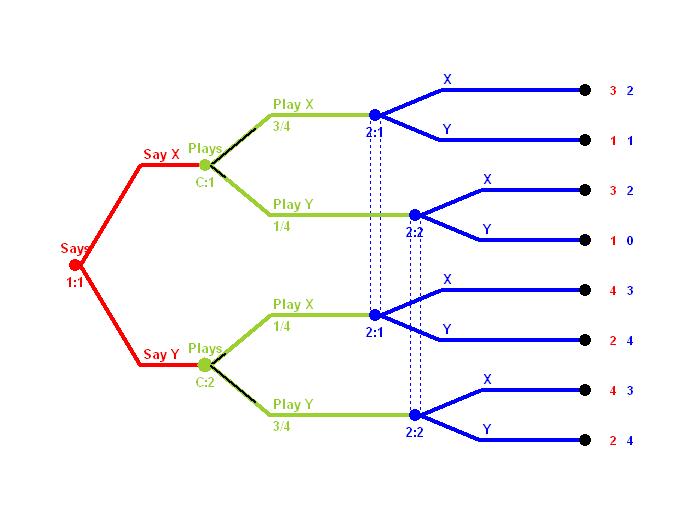
Reading from left to right, says he will play strategy X. With 75% probability he truthfully plays the announced strategy. One has told the truth and Two plays X then the payoffs are (3, 2). Alternatively, if One says he will play X but he lies about it and Plays Y, whereupon Two plays, say, Y and the payoffs are (1, 0). Imagine Player On has two cards; one labeled X and one labeled Y. He says X, but lays the card on the table face down; he alone knows that he has put Y on the table. This is a game of imperfect information since Two doesn't know if she is playing against a truthful opponent or a deceitful opponent. As an interim step we can write the situation as follows:
|
Player One |
||||||
| Truthful (p = 3/4) | Deceitful (1-p = 1/4) | |||||
| Say X and Play X | Say Y and Play Y | Say Y and Play X | Say X and Play Y | |||
| Player Two |
X | 2, 3 | 3, 4 | 3, 4 | 2, 3 | |
| Y | 1, 1 | 4,2 | 4, 2 | 0, 1 | ||
We'll turn this set of side-by-side games into a Normal Form game in which Player 1 chooses from among 'moves' and Player 2 chooses a strategy.
| Player One | |||||
| X(T), X(D) | X(T), Y(D) | Y(T), X(D) | Y(T), Y(D) | ||
| Player Two |
X | 2(3/4)+3(1/4)=9/4, {3, 4} | 2(3/4)+2(1/4)=2, {3, 3} | 3(3/4)+3(1/4)=3, {4, 4} | 3(3/4)+2(1/4)=11/4, {4, 3} |
| Y | 1(3/4)+4(1/4)=7/4, {1, 2} | 1(3/4)+0(1/4)=13/4, {1, 1} | 4(3/4)+4(1/4)=4, {2, 2} | 4(3/4)+0(1/4)=3, {2, 1} | |
Player one still goes first, but Two's information is incomplete since she doesn't know what sort of Player One really is. Look at Player 1. He can never do better than playing Y if truthful and playing X when deceitful. With that in mind, Player Two sees that she should play Y.