The Market for Lemons:  The Good, the Bad and the Ugly

Questions to keep in mind:  Does an informed player have a reason to signal her type to her opponent?  Can the informed player do so credibly?  Suppose the players are a buyer and a seller.  The seller is one of two types: Either a cherry (good quality) or a lemon (bad quality). How are market price and availability affected by buyer uncertainty?  Would buyers only be willing to pay for average quality?  Would a willingness to pay only for average quality cause owners of higher quality goods to withhold their goods from the market?  Will poor quality goods drive high quality goods from the market?

The Good and the Bad

Stu values his first set of wheels at $3200 before accounting for repairs and upkeep.  Thus his net valuation of a cherry is $3000 and his net valuation of the lemon is $1500.  Al feels that a used car has an intrinsic value of $2700.  A good car has a net value to Al of $2500 and a lemon has a net value to him of $1000. We can organize this information in Table 1.

Table 1
		Valuation	Repair Cost	Net Valuation
Lemon	Buyer (Stu)	3200	1700	1500
	Seller (Al)	2700	1700	1000
Cherry	Buyer	3200	200	3000
	Seller	2700	200	2500

To see just where the opportunities for trade exist we will compute for the buyer and the seller the payoffs, G, from trade in lemons and cherries.  First, organize the way in which the payoffs are to be computed in Table 2.  The seller can offer a warranty on the car.

Table 2
		Buyer	Seller
Lemon	Warranty	For p < 2700,  G = 0 since the seller keeps the car when the price is so low.    G = 3200-p for p 2700	For p < 2700, G = 1000     since the net value of holding onto the lemon is 1000 and no trade takes place.   G = p-repair for p 2700
	No Warranty	G = 0 for p < 1000 since the seller keeps the car.  G = 3200-repair-p	G = 1000 for p<1000 G = price for p 1000
Cherry	Warranty	G = 0         for p<2700 since the seller keeps the car if he cannot get at least 2700 for it.   G = 3200-p for p 2700	G = 2500    for p < 2700 since 2500 is the seller's net value from holding onto a cherry.  G = p-repair for p 2700
	No Warranty	G=0 for p<2500 G=3200-p-repair for p2500	G = 2500    for p < 2600   G = p for p 2600

Now use the formulas to compute the actual payoffs and report the results in Table 3.

Table 3
Price	Lemon				Cherry
	Warranty		No Warranty		Warranty		No Warranty
	Buyer	Seller	Buyer	Seller	Buyer	Seller	Buyer	Seller
1000	0	1000	500	1000	0	2500	0	2500
1200	0	1000	300	1200	0	2500	0	2500
1400	0	1000	100	1400	0	2500	0	2500
1500	0	1000	0	1500	0	2500	0	2500
1600	0	1000	-100	1600	0	2500	0	2500
1800	0	1000	-300	1800	0	2500	0	2500
2000	0	1000	-500	2000	0	2500	0	2500
2200	0	1000	-700	2200	0	2500	0	2500
2400	0	1000	-900	2400	0	2500	0	2500
2500	0	1000	-1000	2500	0	2500	500	2500
2600	0	1000	-1100	2600	0	2500	400	2600
2700	500	1000	-1200	2700	500	2500	300	2700
2800	400	1100	-1300	2800	400	2600	200	2800
2900	300	1200	-1400	2900	300	2700	100	2900
3000	200	1300	-1500	3000	200	2800	0	3000
3100	100	1400	-1600	3100	100	2900	-100	3100
3200	0	1500	-1700	3200	0	3000	-200	3200
	Consider the market for lemons with a warranty.  If Stu offers to pay $2800 then the net value of the car to him is $400.  The net value of the trade to Al is $1100.  Indeed, there is non-negative net value to both of them at any price between $2700 and $3200.  At a price below $2700 Al feels that he is better off hanging onto the car, so no trade takes place.  When lemons are offered with no warranty there are opportunities for trade between a price of $1000 and 1500.  Checking the table you can see that at a price of 1500 Stu is indifferent to the trade and Al values the trade at 1500, which is greater than his intrinsic value of the car.				Consider the market for Cherries with a warranty. Trades will take place between a price of $2700, where Al is indifferent to the trade, and 3200, where Stu is indifferent to the trade.  When there is no warranty then trades will take place between $2500, when Al is indifferent, and $3000, where Stu is indifferent.

Let us now introduce the possibility that Stu cannot distinguish a lemon from a cherry.  There are equal numbers of lemons and cherries on Al Gleamer's lot. The most Stu would knowingly pay for a lemon is his valuation of a lemon, $1500.  And the most Stu would knowingly pay for a cherry is his valuation of a cherry, or $3000.  If Stu picks a car at random from Al's lot then 50% of the time he will get a lemon and 50% of the time he will get a cherry.  Therefore Stu will offer to pay for the randomly chosen car. But recall that Al can tell the difference between the cherry and the lemon.  If Stu has picked out a lemon and offers $2250, Al will accept the deal.  But if Stu has picked out a cherry and offers $2250 then Al will decline the offer, since the cherry has a value of $2500 to him. By studying Table 3 Stu is able to discern this behavior and will never offer to pay more than $1500 whenever lemons and cherries are in equal proportions on the lot.  The lemons have driven the cherries out of the market when the buyer cannot distinguish the types of car.

Will this always be the case?  Suppose that only 1/3 of the cars on Al's lot are lemons.  Now the expected value to Stu of a randomly chosen car is .  If Stu happens to choose a lemon and offers $2500 then Al will accept the deal.  When Stu happens to choose a cherry and offers $2500 then Al will be indifferent to the deal.  Indeed, whenever the proportion of lemons on the lot is less than 1/3 there will be some opportunity for both cherries and lemons to be traded.

Now introduce warranties.  Suppose that Al does not offer a warranty on a lemon, but he does sell the cherry with a warranty.  When Stu picks out a car and sees that it has no warranty he will offer $1000.  If he picks out a car that has a warranty with it then he will offer $2700.  In both cases he is just offering the seller's reservation price.

Would Al ever offer a warranty on a lemon?  If he warranted a lemon then he would receive $2700 for the car, since Stu knows that this is the gross value to Al of a cherry.  After paying for repair costs Al would net $1000 on the deal, which is precisely what he would have gotten if he had sold the lemon without the warranty.  Al has no incentive to switch the signal on his lemons.  He also would not remove the warranty from the cherry, since he would then have to price the 'no warranty' cherry at $1000.

What has happened?  We have a separating perfect Bayes equilibrium.  By separating we mean that the prices of the two types of car are different and the two prices depend on the signal.  A pooling equilibrium would mean that Al asks the same price for both types of car.  The perfect Bayes part refers to the way in which Stu revises his prior for the probability of selecting a lemon.  Before seeing the warranty he believes that, say, 1/2 the cars lemons.  Once he sees the warranty affixed to the car he is able to revise his priors.  The posterior probability is P(lemon|warranty) = 0.

To add some excitement to the game we will add elements of offer and counter offer.  There is no warranty.  Al will always sell a cherry for $2500. If the car is a lemon then he will offer to sell the car for $2500 with probability µ and for $1000 with probability (1-µ). Half of Al's cars are lemons.

Stu has decided that he will reject any car with a price above $2500.  He will accept a car priced at $2500 with probability q.  He will always reject a car with $1500 < price < $2500.  He will always accept a car priced at or below $1500.

Stu believes that if a car is priced below $2500 then it is a lemon for sure.  He also believes that cars priced at $2500 or more are lemons with probability ß and cherries with probability (1-ß).

What is the probability that a car is sold if it is a lemon?

1.  We can use Al's pricing rule to express Stu's beliefs in terms of µ by using Bayes rule.

Stu says he believes P(lemon | price 2500) = ß. From Bayes rule we can write this as

P(lemon) = 1/2 since half the cars on the lot are lemons.  Al's rule gives us the other part in the numerator.  There are two ways that a car is sold for $2500 or more under Al's rule: All cherries are sold for $2500, and µ of the lemons are offered for $2500. So the denominator is P(lemon and price $2500) + P(cherry and price $2500) = P(price $2500|Lemon)P(Lemon)+1/2 = µ(1/2)+1/2. So

2. If Stu rejects a price of $2500 then his expected payoff is zero.  If he accepts the price then his expected payoff is (3200-2500-200)(1-ß)+(3200-1700-2500)ß = 500-1500ß.  Since Stu sometimes accepts and sometimes rejects an offer price of $2500, these two expected payoffs must be equal.  Therefore 500-1500ß=0 and ß=1/3, which is the probability of a lemon given its price is $2500 or more.

3. We can use this result for ß to solve for µ, the probability that a car will be offered at a price of $2500 when it is a lemon.

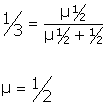
4. If Al's car is a lemon and he offers it for $1000, then that is his expected payoff.  If he offers the the car at a price of $2500 then his expected payoff is 0(1-q)+2500q.  Whenever Al has a lemon he offers it for $1000 sometimes and for $2500 sometimes, so the two expected payoffs ought to be equal. 2500q = 1000, or q = 2/5.

5.  This brings us back to the original question, what is the probability a car is sold if it is a lemon?  A lemon will only be sold if it has a price tag of $2500 on it.  A car will be sold only if it has been offered by Al for a price of $2500 and only if Stu accepts it at a price of $2500.  We can write the question as a probability statement.

Stu's accepting an offer is independent of Al's making an offer, therefore we can write

Making the necessary substitutions we find

or

By randomizing the prices of lemons, Al Gleamer is able to move 20% of them off the lot.  Given the first part of this 'lecture' can you explain what has happened?