Bertrand Price Competition
and
Iterative Elimination of Dominated Strategies
This example considers the Bertrand pricing competition model of a duopoly. The two firms are Randy and Berty, makers of carob seed dog biscuits. The demand curve is Q=6-P, where P is the lower of the two prices. If Berty charges $2 and Randy charges $1, then Randy gets all the sales and is able to sell 5 biscuits. If they charge the same price then they split the market demand; i.e. (6-P)/2. The cost of production is zero. The two can price only in whole dollars: $0, $1, $2,..., $6. The following table shows the quantity demand at each pair of price strategies. The first entry is Randy's quantity and the second is Berty's.
Berty |
||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
R |
0 | 3, 3 | 6, 0 | 6, 0 | 6, 0 | 6, 0 | 6, 0 | 6, 0 |
| 1 | 0, 6 | 2.5, 2.5 | 5, 0 | 5, 0 | 5, 0 | 5, 0 | 5, 0 | |
| 2 | 0, 6 | 0, 5 | 2, 2 | 4, 0 | 4, 0 | 4, 0 | 4, 0 | |
| 3 | 0, 6 | 0, 5 | 0, 4 | 1.5, 1.5 | 3, 0 | 3, 0 | 3, 0 | |
| 4 | 0, 6 | 0, 5 | 0, 4 | 0, 3 | 1, 1 | 2, 0 | 2, 0 | |
| 5 | 0, 6 | 0, 5 | 0, 4 | 0, 3 | 0, 2 | .5, .5 | 1, 0 | |
| 6 | 0, 6 | 0, 5 | 0, 4 | 0, 3 | 0, 2 | 0, 1 | 0, 0 | |
Multiplying the quantities by the appropriate prices gives us the profit payoffs:
Berty |
||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | ||
R |
0 | 0, 0 | 0, 0 | 0, 0 | 0, 0 | 0, 0 | 0, 0 | 0, 0 |
| 1 | 0, 0 | 2.5, 2.5 | 5, 0 | 5, 0 | 5, 0 | 5, 0 | 5, 0 | |
| 2 | 0, 0 | 0, 5 | 4, 4 | 8, 0 | 8, 0 | 8, 0 | 8, 0 | |
| 3 | 0, 0 | 0, 5 | 0, 8 | 4.5, 4.5 | 9, 0 | 9, 0 | 9, 0 | |
| 4 | 0, 0 | 0, 5 | 0, 8 | 0, 9 | 4, 4 | 8, 0 | 8, 0 | |
| 5 | 0, 0 | 0, 5 | 0, 8 | 0, 9 | 0, 8 | 2.5,2.5 | 5, 0 | |
| 6 | 0, 0 | 0, 5 | 0, 8 | 0, 9 | 0, 8 | 0, 5 | 0, 0 | |
Note the symmetry in the two tables. This makes our analysis of the game easier since we need only consider either the rows or the columns and know that the other player will arrive at symmetric conclusions.
1. What price strategies are dominated? Consider $4, $5, $6 and $0.
2. Are there any others that are dominated?
3. Suppose that there was only one firm in this industry. For this purpose we'll suppose that Berty has a monopoly. What will be his profit maximizing quantity and price?
First invert the demand curve:
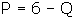
Multiply by quantity to get total revenue, or profit since cost per unit produced is zero.
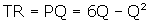
Maximum profit will occur where the profit function has a slope of zero.
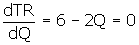
The quantity at which the slope is zero is then
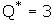and the corresponding price is P*=3.
4. Why wouldn't either firm charge a price above the monopoly price? When could a firm in this duopoly charge a price above the monopoly price and still make a positive profit? What would happen to those profits if the firm reverted to the monopoly price instead?
5. As a result of your answer to the first question we can cover up the cells corresponding to prices of $0, $4, $5, and $6. What can we say about the monopoly price strategy of $3 after we have taken out the dominated strategies we have already identified?
6. On the basis of what you found in question 5, what is the IEDS solution to this game?
7. On the basis of this example, what do you conclude about the consumer and price competition? Are there any laws of the land that try to promote price competition as an end, or at least try to prevent monopoly pricing and collusion?
