

Tragedy of the Commons
First definitions:
Modern examples of a common resource:
Critical characteristics of a commons
Externalities
| Consumption | Production | |
| Current |  |
 |
| Future |  |
 |
The tragedy of the commons and A Civil Action
In Woburn, MA Beatrice Foods and W R Grace both had plants that as a by-product of their output produced toxic chemicals. Rather than pay to store, haul away and treat those chemicals it became their practice to pour those chemicals on the ground. While Grace and Beatrice avoided part of the cost of production it was a cost that was imposed on the community in the form of contamination of the local ground water. The toxic chemicals leached out of the ground and into the water system, from which the residents drew their drinking water.
A Model of the Over-use of the Commons
Two players, Beatrice and Grace, consume cB and cG
units of the common resource, y, such that ![]() . If their combined consumption today exceeds y then cB
= cG = y/2. Whatever they don't consume of y today is available for
consumption tomorrow and is calculated as y - cB - cG .
In the future each firm gets (y - cB - cG )/2 for its own
consumption.
. If their combined consumption today exceeds y then cB
= cG = y/2. Whatever they don't consume of y today is available for
consumption tomorrow and is calculated as y - cB - cG .
In the future each firm gets (y - cB - cG )/2 for its own
consumption.
The utility from the consumption of the resource is given by ln(c), and looks like:

The graph is the same for both firms.
Beatrice's problem is to choose its utility maximizing consumption given Grace's choice. Beatrice''s utility from consumption in the two periods is
and she must choose her consumption so that
The first derivative with respect to Beatrice's consumption is
with a little algebra
|
||
We find Beatrice's best response in consumption to Grace's choice is
The graph of this looks like

The problem is symmetric so we have
![]() and the graph looks like
and the graph looks like

Putting Beatrice's and Grace's best response functions together we get the following

Solving the pair of best response functions for the two unknowns
If we solve the second equation for cB, then we can set the two equal and solve for cG, then substitute back to get cB. After all of the manipulation we get
| |
|
The firms consume 2/3 of the resource in the first period and 1/3 in the second period.
By contrast, let us see what happens when we maximize aggregate utility over the two periods. We'll define aggregate utility as the sum of the utility for the two firms over the two periods.
So now the problem is to
To find the maximum we take the derivatives with respect to cB and cG, set the results to zero, and solve for the two unknowns, cB and cG. The two derivatives are known as the 'first order conditions'. They are

|
||
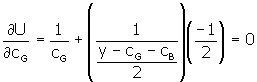 |
If you solve this pair of equations for the two unknowns then
We now see that each firm consumes 1/4 of the resource in each period, whereas they each had previously consumed 1/3 of the resource in the first period. Why do they consume less? In the first phase when Beatrice and Grace choose independently, if Beatrice reduces consumption by 1 now then she will only get to consume half of that unit in the next period. So, her incentive is to not defer consumption. The problem is worse in a big population since the unit of consumption of the common resource you give up today is shared with everyone tomorrow.