Bankruptcy: Liberty Bell Beer and its
Creditors
When Liberty Bell Beer declares bankruptcy its individual creditors
can no longer appropriate its assets for themselves. Instead the bankrupt firm's
assets are frozen and a plan is worked out to settle the claims. The creditors might sell
the company's assets and apportion the proceeds, they might refinance the company,
or they might take over the company and operate it themselves.
There is a feature of the bankruptcy law called voidable preferences. Under this principle
the bankrupt firm can recapture any transfers it made to its creditors within up to 90
days of having declared bankruptcy. The legal view of the principle of voidable
preferences is that it strengthens the law's protection of creditor assets.
Liberty Bell has assets of $15 millions. There are three
investors, Hughey, Dewey and Cheatum, who financed the startup brewery; each one invested
$10 millions, for a total of $30 millions. Clearly, Liberty Bell is in
trouble. If it declares bankruptcy and sells its assets in an orderly fashion then
each creditor gets back $5 millions.
If Hughey acts preemptively and forces Liberty Bell to liquidate
its assets at fire sale prices then she can recover her entire loan and there will be $2
millions left over to be split between Dewey and Cheatum in a later bankruptcy. Of
course either Dewey or Cheatum could try the same tactic and leave the other partners
holding the bag.
If two or more partners try to make a preemptive grab then Liberty
Bell is immediately forced into bankruptcy, voidable preferences kick in, and the firm's
assets are sold at fire sale prices. The result is that each partner gets $4
millions.
| Payoffs Hughey, Dewey,
Cheatum |
| # of other creditors making a grab
with |
0 |
1 |
2 |
| Payoff
to Hughey when |
Hughey grab |
10 |
4 |
4 |
| Hughey refrains |
5 |
1 |
4 |
The same table applies to each of the other players. Grabbing is
the dominant strategy for each of them. Apparently voidable preferences law does
nothing to deter creditors from dismantling the firm.
Are there circumstances under which the principle of voidable
preferences has a deterrent effect? Let's change the game so that grabbing is not
the dominant pure strategy.
If Hughey makes a grab then instead of getting $10 she nets only
$9, since it costs $1 to instigate the grab for the firm. There is still $1 left over for
each of the other two partners since the firm sells for $12.
If Hughey and one other person make a grab then the firm goes into
bankruptcy, voidable preferences are invoked, and the firm is put up for sale right away
at $12. Each grabbing partner gets just $3 due to the costs of having initiated the
grab; each of the grabbing firms spends $1 in the liquidation. The refraining partner
takes away $4.
If one partner makes a grab and Hughey refrains then she gets
$1.
Finally, if Dewey and Cheatum spend $1 each to force the sale of
the firm for $12 then they each net $3, and Hughey gets $4.
If Hughey and both of the other partners grab simultaneously then
each firm nets $3.
| Hughey's payoffs |
| # of other creditors making a grab |
0 |
1 |
2 |
| Payoff
to Hughey when |
Hughey grab |
9 |
3 |
3 |
| Hughey refrains |
5 |
1 |
4 |
If everyone concedes then each investor gets $5 M. As
before, if everyone grabs then the outcome is worse than if everyone
refrains. If at least one opponent refrains then it is better to grab. On
the other hand if the other two partners are grabbers then it is better for Hughey to
concede.
Even though there is no dominant pure strategy, there may be a
mixed strategy equilibrium. Let each of the other players refrain with probability p
and grab with probability 1-p. Hughey's expected payoff is now
| Hughey faces a mixed strategy played by her competitors |
| Dewey and Cheatum |
Probability |
Hughey grabs |
Pr x Payoff |
Hughey refrains |
Pr x Payoff |
| Both refrain |
p2 |
9 |
9p2 |
5 |
5p2 |
| One refrains |
2p(1-p) |
3 |
6p(1-p) |
1 |
2p(1-p) |
| Both grab |
(1-p)2 |
3 |
3(1-p)2 |
4 |
4(1-p)2 |
| Expected Payoff |
|
|
3+6p2 |
|
4-6p+7p2 |
Any mixed strategy that Hughey plays should leave her indifferent
between the outcomes 3+6p2 and 4-6p+7p2. Setting these equal
to each other yields p2 - 6p + 1 = 0. We can use the quadratic formula, 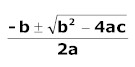 , to find the values of p that solve this
equation. p = 3-2(2)½ = .20. Since the game is symmetric each of
the three investors arrives at the same conclusion regarding p. The consequence is
that the probability of all three refraining is only .23 = .008, in spite of
the principle of voidable preferences!
, to find the values of p that solve this
equation. p = 3-2(2)½ = .20. Since the game is symmetric each of
the three investors arrives at the same conclusion regarding p. The consequence is
that the probability of all three refraining is only .23 = .008, in spite of
the principle of voidable preferences!
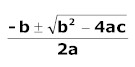 , to find the values of p that solve this
equation. p = 3-2(2)½ = .20. Since the game is symmetric each of
the three investors arrives at the same conclusion regarding p. The consequence is
that the probability of all three refraining is only .23 = .008, in spite of
the principle of voidable preferences!
, to find the values of p that solve this
equation. p = 3-2(2)½ = .20. Since the game is symmetric each of
the three investors arrives at the same conclusion regarding p. The consequence is
that the probability of all three refraining is only .23 = .008, in spite of
the principle of voidable preferences!