In the market for electronic games the vendors try to give the user as realistic an experience as possible, in the confines of a virtual world.  During the early part of the year the leading makers have to decide on the sort of game machine they are going to bring to market.  They can spend a lot on research and development and bring a large, full featured model to market.  Or they can make a small commitment to R&D and bring a small, limited feature model to market.  They always get their work done prior to the annual electronics trade show in Las Vegas, at which time they reveal to the world their newest product.  After the trade show they return to their corporate offices and decide on a price for their product; either hi or lo.  The sequential and simultaneous aspects of the game are shown in the extensive form below:

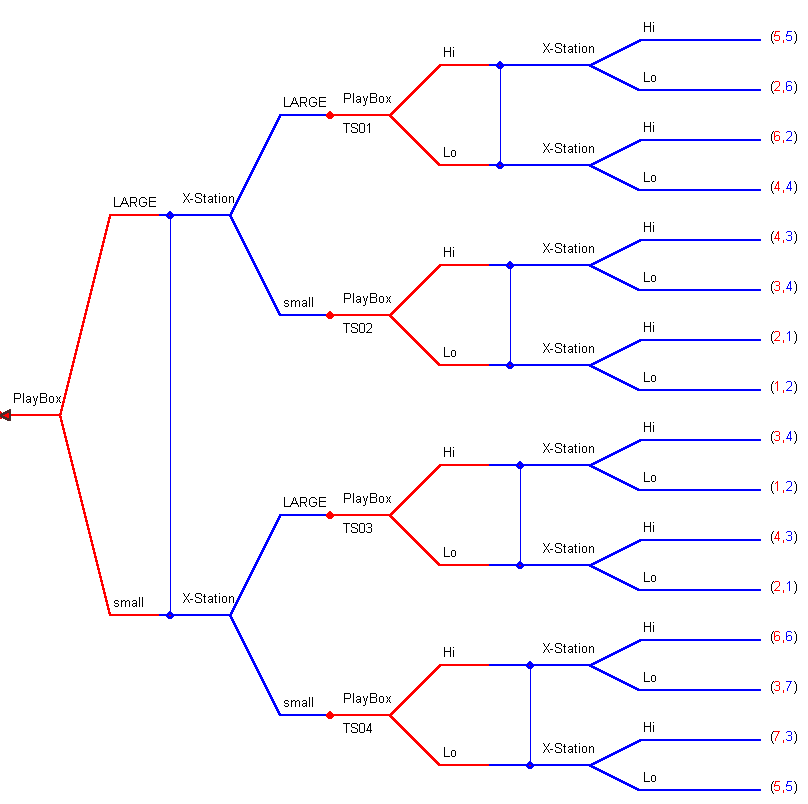
In simultaneous moves PlayBox and X-Station must commit to either a large system or a small system.  They reveal their picks and the results of their endeavors at the annual trade show.  The trade show occurs at the nodes TS01 through TS04.  Subsequent to the trade show they are again involved in a simultaneous play game of choosing the price for their system.

The sub-game beginning with node TS01 is a prisoner's dilemma.  Each firm has a dominant strategy to price low, although their combined payoff would be greater if they could collude and price high.  The pricing sub-game that follows node TS04 is also a prisoner's dilemma.  The solution is that both firms price low, although their combined payoff would be greater if the both priced high.

The imperfect information sub-game at TS02 also has a dominant strategy solution, although it is not a prisoner's dilemma. X-Station's dominant strategy is to price low.  Given that X-Station's dominant strategy is to price low, it is PlayBox's dominant strategy to price high.  Note that we get to TS02 only when PlayBox builds a large system and X-Station builds a small system.

The imperfect information sub-game at TS03 is like the one at TS02.  This time X-Station's dominant strategy is to price hi and PlayBox's dominant strategy is to price low.  We can get to TS03 only if PlayBox builds a small system and X-Station builds a large system.

Once we trim off the unused branches of the pricing sub-games, the remaining extensive game tree looks like:

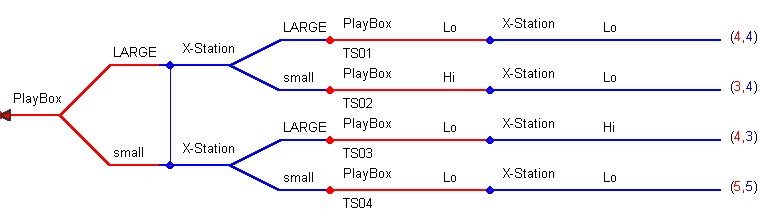
Now we see that for X-Station small is weakly dominant over large {4=4 and 5>3}.  With that in mind, PlayBox concludes that it will play small as its dominant strategy {5>3}. The sequence of plays is PlayBox: small, Low and X-Station: small, Low.

Some further ideas about research and development explored by economists using game theory:

In 1957 Robert Solow (a Nobel Laureate) observed that only 10% of U.S. growth could be accounted for by the rise in the capital-labor ratio.  Even more recent studies that account for the improving quality of the labor force report that there remains a large unexplained part of economic growth.  One possible conclusion is that technical progress resulting from research and development accounts for the unexplained portion of growth.

The research function is usually broken into three stages:  Basic research results in new, fundamental knowledge.  Applied research refers to engineering the product; getting it from a prototype to something that can be mass produced.  Development is the process of getting the product to market.  Once a new product has been brought to market its diffusion results in economic growth.  Throughout this taxonomy innovations can be either new products or new processes.

Schumpeter was instrumental in bringing the importance of R&D and innovation to the attention of economists.  His thesis can be summarized in two arguments: Monopolies are natural breeding grounds for R&D.  And, one must accept the creation of monopolies in order to induce firms to undertake risky R&D.  Needless to say, Schumpeter's propositions proved fertile ground for economic research.

Using game theory economists have been able to show that a monopolist has the least incentive to innovate.  Firms in a competitive market have more incentive to innovate than the monopolist, and a central planner has the greatest incentive to innovate.

Economists have used game theory to study patent races.  In such models firms influence the probability of winning a patent by spending more on R&D.  Increased spending increases the probability of beating one's rivals to the patent office.  In the previous paragraph it was suggested that the potential entrant has more incentive to innovate than the monopolist.  To avoid this the monopolist may spend more on R&D in order to win the race, even though they may never use the new product or process!