Backward Induction
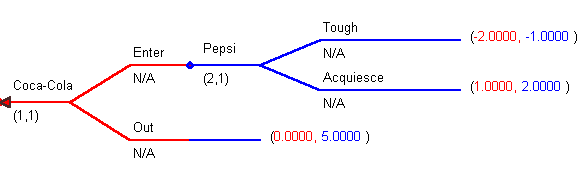
What is a reasonable sequence of moves in the Coke-Pepsi game we saw in the previous section?
The idea behind backwards induction is for the player to pick the most reasonable course of action at a given node. We always work from right to left.

Begin by writing the game in its strategic form and finding the Nash equilibria:
| Pepsi | |||
| Tough | Accommodate | ||
| Coca-Cola | Enter | -2, -1 | 1, 2 |
| Out | 0, 5 | 0, 5 | |
There are two Nash equilibria (the teal cells), but are they both plausible? To find them write out the best responses for both players. Does it make sense for Pepsi to commit the resources to play Tough when Coke stays out of the market? Tough is a best response to Out only because Coke never uses it. To see why this occurs we need to learn about backward induction.
Begin by considering Pepsi's decision. Once we are at the node labeled Pepsi, the choice is Tough or Acquiesce. Since Tough results in a loss of -1 and Acquiesce results in a gain of 2, Pepsi will choose to acquiesce. Coke can see this as well. Since Coke knows that Pepsi will Acquiesce, Coke's best course of action is to Enter. Staying Out will earn it 0 and entering the market will ultimately earn it 1.
Let's look at a more complicated game involving Coke and Pepsi. The game is extended another round in which after observing Pepsi's (Tough, Acquiesce) stance Coke can itself choose to be Tough, Acquiesce, or go Out of the market.
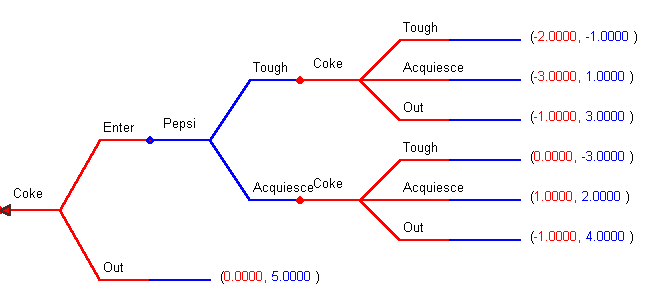
Working backwards, Coke looks at Pepsi's Tough play and should choose to go Out of the market since it then only loses -$1. If Coke sees Pepsi Acquiesce then it should itself Acquiesce and earn $1. Coke will never play Tough.
Pepsi knows that when it plays Tough Coke will exit, and Pepsi's payoff will be $3. Compare this to its payoff when it Acquiesces and Coke then also Acquiesces; Pepsi earns $2 and Coke earns $1. Given that Pepsi is in the enter branch, Pepsi's best choice is to act Tough; it knows Coke's response will be to go Out of the market.
Going back now to the root, Coke reasons backwards: Coke knows that if it enters, then Pepsi will play Tough and Coke's best response is to go Out. Hence, Coke's best initial play is to Stay Out since it loses 0 instead of -1.
Let's set this game up in its strategic or normal form. The only strategies available to Pepsi are either Tough or Acquiesce. We need to list all of the strategies available to Coke. These strategies are in the nature of complete conditional plans. Each of Coke's strategies will be represented by a triplet in which the first character indicates Enter or stay Out. The second character indicates how Coke should behave in the face of a Tough response by Pepsi. The third character will tell us how Coke should react when Pepsi Acquiesces. The strategies are:
Coke's available strategic plans |
|
| ETT | Enter, then Play Tough against Pepsi's Tough, or Play Tough against Pepsi's Acquiesce |
| ETA | Enter, then Play Tough against Pepsi's Tough, or Play Acquiesce against Pepsi's Acquiesce |
| ETO | Enter, then Play Tough against Pepsi's Tough Play Out against Pepsi's Acquiesce |
| EAT | Enter, then Play Acquiesce against Pepsi's Tough Play Tough against Pepsi's Acquiesce |
| EAA | Enter, then Play Acquiesce against Pepsi's Tough Play Acquiesce against Pepsi's Acquiesce |
| EAO | Enter, then Play Acquiesce against Pepsi's Tough Play Out against Pepsi's Acquiesce |
| EOT | Enter, then Play Out against Pepsi's Tough Play Tough against Pepsi's Acquiesce |
| EOA | Enter, then Play Out against Pepsi's Tough Play Out against Pepsi's Acquiesce |
| EOO | Enter, then Play Out against Pepsi's Tough Play Out against Pepsi's Acquiesce |
| O | Enter, then |
Actually, the last row should be expanded to encompass all of the possible triplets when Coke initially plays Out. Since Out is the initial choice it doesn't make much sense to outline the responses to Pepsi's Tough or Acquiesce choice.
Now set up the payoff matrix
Pepsi's Strategy |
|||
| Tough | Acquiesce | ||
| Coke's Strategic Plans | ETT | -2, -1 | 0, -3 |
| ETA | -2, -1 | 1, 2 | |
| ETO | -2, -1 | -1, 4 | |
| EAT | -3, 1 | 0, -3 | |
| EAA | -3, 1 | 1, 2 | |
| EAO | -3, 1 | -1, 4 | |
| EOT | -1, 3 | 0, -3 | |
| EOA | -1, 3 | 1, 2 | |
| EOO | -1, 3 | -1, 4 | |
| O | 0, 5 | 0, 5 | |
Best Responses |
|
| Coke's Behavior | Pepsi's Behavior |
| bCoke(ToughPepsi) = O | bPepsi(ETTCoke) = T |
| bCoke(AcquiescePepsi)=EOA, | bPepsi(ETACoke) = A |
| ETA, EAA | |
| bPepsi(ETOCoke) = A | |
| bPepsi(EATCoke) = T | |
| bPepsi(EAACoke) = A | |
| bPepsi(EAOCoke) = A | |
| bPepsi(EOTCoke) = T | |
| bPepsi(EOACoke) = T | |
| bPepsi(EOOCoke) = A | |
| bPepsi(OCoke) = A, T | |
While there are three Nash equilibria, only one of them is the solution to the game; The first two are Coke plays either ETA or EAA and Pepsi plays A. The third is that Pepsi looks tough and Coke stays out.
The method of backward induction is sometimes known as the rollback method or Zermelo's algorithm.
[Commitment ]