  |
Extensive Form Games with Perfect Information: |
 |
  |
Extensive Form Games with Perfect Information: |
 |
Example 1: Pepsi and Coke are the largest soft drink manufacturers in the world. They compete in many geographic markets. They also compete in product markets of two types. The first type is in flavors; a form of product differentiation not unlike ready to eat cereal. The second type of market is in packaging. You can buy Pepsi at a fountain, with your Big Mac, or packaged in a can or bottle at a 7-11 convenience store. In this discussion we will focus on entry into a geographic market.
Pepsi already sells its product line in Erehwon and Coke is contemplating entry into the market; they can either enter or stay out. If Coke enters then Pepsi can either fight an aggressive marketing war or remain passive and share the market. After entry, once Coke sees Pepsi's marketing response they too can either fight or be passive and share the market peacefully.
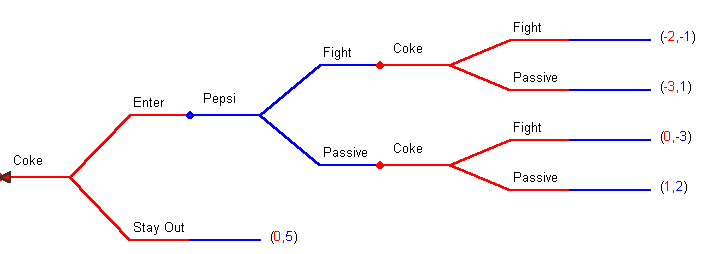
We can put this game in its strategic form. Remember that a strategy is a complete, conditional plan. Pepsi will have just two strategies. Technically there are four shown in the table below.
| <FightEntry, FightOut> | Fight when Coke enters, Fight when Coke stays out |
| <FightEntry, PassiveOut> | Fight when Coke enters, Passive when Coke stays out |
| <PassiveEntry, FightOut> | Passive when Coke enters, Fight when Coke stays out |
| <PassiveEntry, PassiveOut> | Passive when Coke enters, Passive when Coke stays out |
Since fighting and remaining passive when Coke stays out are not operative decisions, we can reduce Pepsi's strategies to Fight and Passive
Coke will have eight strategic plans, shown in the following table:
| <Enter, FightFight, FightPassive> | Enter, Fight in response to Pepsi's Fight stance, Fight in response to Pepsi's Passive stance. |
| <Enter, FightFight, PassivePassive> | Enter, Fight in response to Pepsi's Fight, Passive in response to Pepsi's Passive |
| <Enter, PassiveFight, FightPassive> | Enter, Passive in response to Pepsi's Fight, Fight in response to Pepsi's Passive |
| <Enter, PassiveFight, PassivePassive> | Enter, Passive in response to Pepsi's Fight, Passive in response to Pepsi's Passive |
| <Out, FightFight, FightPassive> | Stay Out, Fight in response to Pepsi's Fight stance, Fight in response to Pepsi's Passive stance. |
| <Out, FightFight, PassivePassive> | Stay Out, Fight in response to Pepsi's Fight, Passive in response to Pepsi's Passive |
| <Out, PassiveFight, FightPassive> | Stay Out, Passive in response to Pepsi's Fight, Fight in response to Pepsi's Passive |
| <Out, PassiveFight, PassivePassive> | Stay Out, Passive in response to Pepsi's Fight, Passive in response to Pepsi's Passive |
Having enumerated all of the conditional plans we can put together the strategic form of the game:
|
Pepsi |
|||
| Fight | Passive | ||
|
Coke |
<Enter, FightFight, FightPassive> | -2, -1 | 0, -3 |
| <Enter, FightFight, PassivePassive> | -2, -1 | 1, 2 | |
| <Enter, PassiveFight, FightPassive> | -3, -1 | 0, -3 | |
| <Enter, PassiveFight, PassivePassive> | -3, -1 | 1, 2 | |
| <Out, FightFight, FightPassive> | 0, 5 | 0, 5 | |
| <Out, FightFight, PassivePassive> | 0, 5 | 0, 5 | |
| <Out, PassiveFight, FightPassive> | 0, 5 | 0, 5 | |
| <Out, PassiveFight, PassivePassive> | 0, 5 | 0, 5 | |
Things to observe about the game as shown:
1. Using IEDS: For Coke, any of the Stay Out strategies weakly dominate EFF and
EPF. On seeing this Pepsi will conclude that its Passive strategy
dominates Fight. Then Coke sees that it is indifferent between EPP and EFP.
2. There are three Nash equilibria: a. Pepsi plays Fight and Coke chooses to
stay out. b. Coke plays EFP and Pepsi plays Passive. c. Coke plays EPP and
Pepsi plays Passive. The observed outcomes in 2.b. and 2.c. are the same.
3. The IEDS solution is a Nash equilibrium and is also the solution to the
extensive form of the game using backward induction.
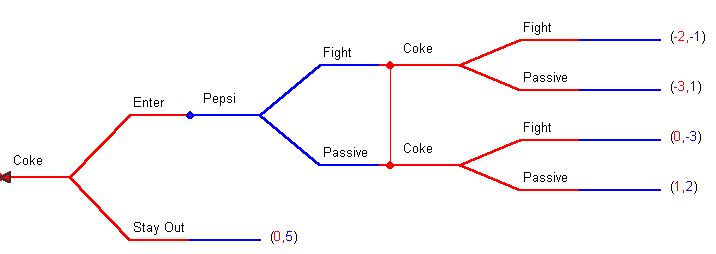
Example 2: In this version of the model Pepsi and Coke must make their Fight - Passive decision simultaneously. That is, there is imperfect information. However, the payoffs are such that the solution is equivalent to using IEDS in the strategic form of the game.
Example 3: In this final version of the game information is imperfect, but the payoffs are such that it is not possible to use dominated strategies to find a solution to the game.
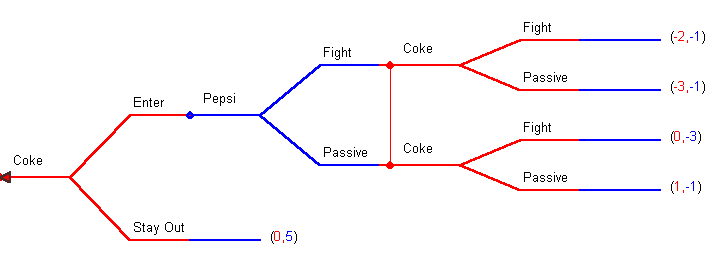
In the normal form of the game, shown below, EFF is dominated by EFP and EPF is dominated bu EPP. In addition EFP dominates EPP. Any of the Stay Out strategies dominates EFP, which after IEDS is the only "Enter" strategy that remains for Coke.
Apparently the player with whom we start IEDS doesn't matter. Begin the process with Pepsi instead of Coke and observe that Fight weakly dominates Passive. At this point any Stay Out strategic plan dominates any Enter plan.
We conclude that there are at least four equilibria in the game. Since all of the equilibria require Coke to Stay Out and Pepsi to Fight and the payoffs are the same for all of them it seems that the four equilibria are observationally equivalent.
Using 'best response' two additional equilibria are revealed at <EFP, P> and <EPP, P>.
|
Pepsi |
|||
| Fight | Passive | ||
|
Coke |
|||
| <Enter, FightFight, PassivePassive> | -2, -1 | 1, -1 | |
| <Out, FightFight, FightPassive> | 0, 5 | 0, 5 | |
| <Out, FightFight, PassivePassive> | 0, 5 | 0, 5 | |
| <Out, PassiveFight, FightPassive> | 0, 5 | 0, 5 | |
| <Out, PassiveFight, PassivePassive> | 0, 5 | 0, 5 | |