Kuhn's Theorem
Also attributed to Zermelo
Every sequential game with perfect information has a Nash equilibrium.

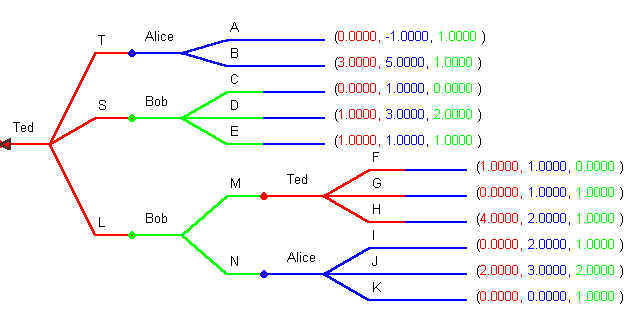
The theorem can be proved using backward induction. In the above game with Bob, Ted and Alice consider the rightmost nodes first, starting at the bottom. The terminal node at the bottom belongs to Alice; she will play J. The node above her belongs to Ted; he will play H. The next terminal node above him belongs to Bob; he will play D. Above him is Alice and she will play B. After trimming the branches that won't be played we get:
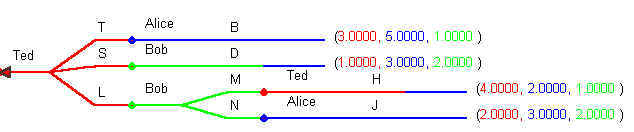
Trim the game tree again, from right to left. Now Bob has the rightmost decision node. He will play N and the trimmed tree looks like:

Now we have rolled the game tree back to Ted's initial move. At this point Ted's dominant strategy is to play T. The game tree, after eliminating the dominated strategies in the terminal nodes, looks like:

As long as we know the ordinal ranking of the payoffs we could use the same rollback solution method to any perfect information game.
Note that backward induction doesn't find all of the Nash equilibria. An example is the following game between Sally and Jesse.
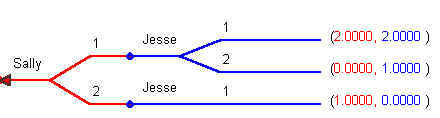
The rollback solution to the game is for Sally to play 1 and for Jesse to then play 1. However, when you look at the strategic form representation of the game then you can see that there are two Nash equilibria.
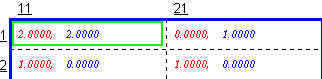
Check the best response table to find them.
| Sally | Jesse |
| bS(11J)= 1 | bJ(1S) = 11 |
| bS(21J) = 2 | bJ(1S) = 11 |