Information and Extensive Form Games

A perfect information game is one in which there is NO Information Set.  In such a game each player knows exactly what her opponent has done at the preceding node.  When it is a game of imperfect information then a player doesn't know with certainty what strategies have been played at preceding nodes.  To clarify the differences we can look at some constructs using GAMBIT. 

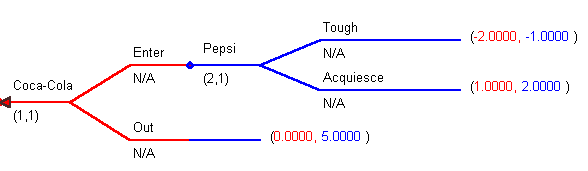
In the following game suppose that Pepsi is already in the Singapore market and Coke is deciding whether or not they will Enter, or stay Out.  Pepsi would then decide whether they will adopt a Tough defensive response or Acquiesce. The payoffs are shown to the right of the terminal nodes.  At the time that they must choose between Tough and Acquiesce Pepsi knows with certainty what Coke has done.  This is a game of perfect information.

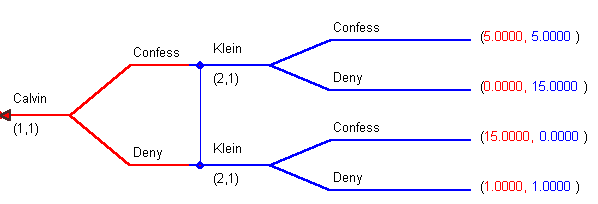
To distinguish the Coke-Pepsi example from a game of imperfect information we revisit the Prisoner's Dilemma.  Calvin and Klein have been arrested for the crime of poor taste.  If Calvin confesses and implicates a Klein in denial, then Calvin gets off and Klein serves 15 years; and vice versa.  If they both confess then they each serve five years.  If they both deny their guilt then they both go to jail for a year.  The information sets available to them are labeled in parentheses beneath their names.  Calvin's information set is (1,1), the first digit identifies him as player 1 and the second digit tells us which of his information sets he is using.  Since there is nothing to his left he knows nothing about Klein's play.

Klein has information set (2,1).  He is player 2 and he is using his information set 1.  You will note that he is using the same information set at both of the decision nodes that apply to him.  That is because he doesn't know whether or not Calvin has confessed.  Instead of the elliptical balloon previously used to represent Klein's information set we just tie his two decision nodes together with the vertical blue line.      

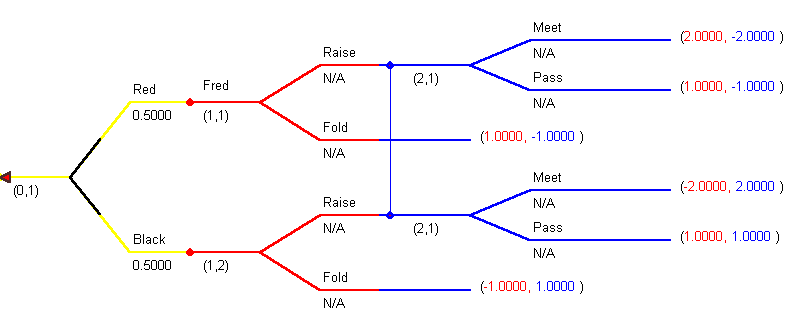
In this third example Fred and Francine are playing a card game.  Fred is dealt a card.  It can be red or black with equal probability.  This is randomness introduced by an unknown state of nature at the start of the game. Once he sees the color of the card Fred can either raise his bet or fold.  Once she sees whether or not Fred has raised his bet, Francine can either meet the bet or pass.  The only thing that Francine doesn't know when she makes her decision is what color card Fred has drawn.  If Fred draws a Red, raises his bet and Francine meets it then she loses $2 and Fred wins it. If Fred draws a black and elects to bluff by raising his bet and Francine passes then they each win a dollar.  We have joined Francine's nodes together by a vertical line to show that her information is something other than perfect.  Although she knows what strategy Fred has played, she doesn't know if he is holding a red card.  We say that this is a game of incomplete information.