Solving Extensive Form Games
Thus far we have considered strategic form games that were
presented in the form of two-way tables. Such representations are awkward for
picturing games in which the players move sequentially. In order to represent
sequential games we need to explore extensive form games. There are two graphical
representations of extensive form games. Either representation is known as a game
tree.
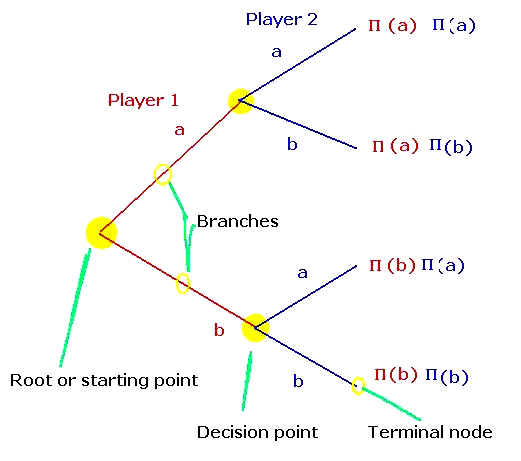 |
| In the first panel we have a game tree representing
a sequential game. The starting point of the game or root of the tree is at the left
edge of the picture. Player 1's two moves are a or b and are
represented as two branches coming off the root. At the ends of the branches for Player 1 are the decision points for Player
2. The relevant decision point for Player 2,
in blue, depends on the observed choice made by Player 1.
Player 2 can also choose between strategy a and strategy b. The
payoffs, denoted P(a) and P(b), are at the terminal nodes of the game
tree. When it is her turn to move Player 2 knows what
choice has been made by Player 1. This is denoted by the fact that Player 2's
branches are explicitly attached to the nodes of Player 1's branches. |
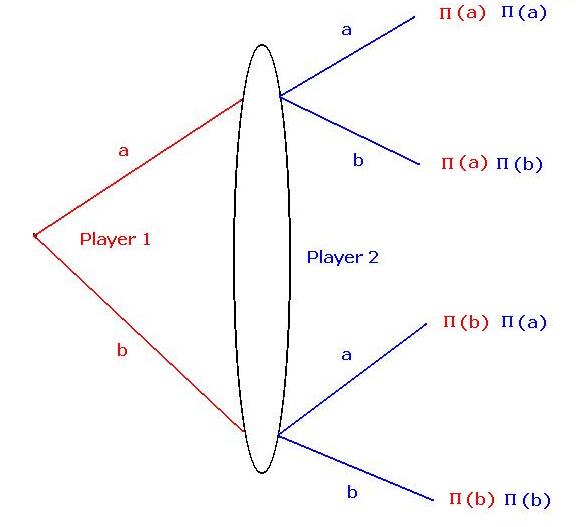 |
| The terminology of this game tree is the same as
that for the previous game tree. There is one important difference. The
branches for Player 2's decisions are not attached directly to the branches for Player
1. At the time player 2 makes her decision she doesn't know what strategy has been
chosen by Player 1.
The ellipse is known as the information set. Contained in
the information set is an enumeration of the strategies available to Player 1 and the
payoffs associated with those strategies. Also ocntained in the information set is
an enumeration of the strategies available to Player 2 and the associated payoffs.
In effect the information set contains all of the data necessary for the players to make
their decisions simultaneously. |
The conditions necessary to represent a game as a tree
- A single starting
point
- No cycles
- One way
to proceed
Strategies: A player's strategy is a complete conditional plan of action.
Mixed Strategies: A mixed strategy is a probability
distribution over the pure strategies, the support, that might be played.
Chance Nodes: A chance node
is a way to introduce uncertainty into a game beyond the uncertainty created by the
players' use of mixed strategy. An example might be different states of nature that
may or may not be resolved before the players make their choices.

