George and Gina

George and Gina are sweethearts. After dating for a mere ten years, George must decide on a location for his anniversary dinner with Gina. Once the choice is made it is known to both of them. The choices are Perrier, a very up-scale restaurant in Philadelphia, and the local McDonald's.

Being a very deliberate fellow, George must also decide beforehand on appropriate dinner conversation for each venue. If he takes Gina to Perrier then George feels that he must either formally propose, or prevaricate and postpone the big announcement for another year. If he takes Gina to McDonald's then George can still propose, but if he chooses not to propose then he better have something of interest to Gina that he can talk about, namely stocks. George's topic of conversation will not be known to Gina until they are in the restaurant.

Gina thinks it is about time that she and George settle on a future for their relationship. Indeed, she has decided that she will preempt George's chosen topic and either accept or refuse his offer of marriage should she find herself dining at Perrier. It is so inconceivable to her that George would be so crass as to propose in McDonald's that she will prepare herself to discuss either football or bonds should she find herself there.

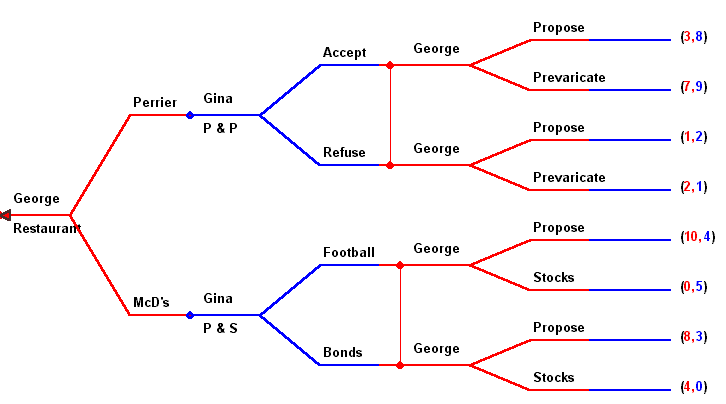
What are the subgames in this marriage game between George and Gina? There is one at the node labeled P&P. Fill in the payoffs and find the Nash equilibria.

There is another subgame at the node labeled P & S. Fill in the payoffs and find the Nash equilibria.

The entire game is also a subgame. Fill in the remaining payoffs and find the Nash equilibria. In working with the following normal form game recall that a strategy is a complete contingent plan. This means that George must have a plan of action in the event that he finds himself at any node in the game. Therefore each of his strategies consists of three possible moves.

The Normal Form of George's and Gina's Mating Dance
				Gina
				Strategy 1		Strategy 2		Strategy 3		Strategy 4
				At P&P	At P&S	At P&P	At P&S	At P&P	At P&S	At P&P	At P&S
				Accept	Foot	Refuse	Foot	Accept	Bonds	Refuse	Bonds
George	Perrier	Propose	Propose	3, 8						1, 2
	Perrier	Prevar	Propose	7, 9
	Perrier	Propose	Stocks	3, 8
	Perrier	Prevar	Stocks	7, 9
	McD	Propose	Propose	10, 4		10, 4		8, 3		8, 3
	McD	Prevar	Propose	10, 4
	McD	Propose	Stocks	0, 5
	McD	Prevar	Stocks	0, 5						4, 0
	At Rest	At P&P	At P&S

You should have found a Nash equilibrium in each of the two subgames. In the normal form of the entire game there is only one subgame perfect equilibrium. Explain why one of the subgame Nash equilibria is not a subgame perfect equilibrium.

Subgame at Propose and Prevaricate (P & P)
		Gina
		Accept	Refuse
George	Propose
	Prevaricate

Subgame at Propose and Stocks (P & S)
		Gina
		Football	Bonds
George	Propose
	Prevaricate