Contracting is a part of everyday economic life.
Firms and their employees
Doctors and patients
Parents and children
Any contractual relationship has two phases
A contracting or negotiating phase in which the players set the terms of the contract
An implementation phase during which the contract is carried out and enforced
Negotiated contracts involve the trade of goods, services and/or money. Trade can create value. Avery has a pizza and Bart has a TV. If they only consume what they have then Avery doesn't get to watch the World Series and Bart goes hungry. If Bart sells some TV time to Avery for half the pizza then they may both be better off.
As we saw in the story of Tommy, Penny and Nicky at the start of the semester, creating value is one thing and dividing value is another.
The outcome of bargaining is either an agreement about the terms of mutual cooperation, or it is a conflict when no agreement is reached.
For purposes of analysis an outcome can be characterzed as a vector x = (x1, x2) in which x1 is the commodity bundle going to person 1 and x2 is the commodity bundle going to person 2. These are the physical outcomes.
Another approach would be to state the outcome in terms of the utility that each person gets from her commodity bundle. That is, u = (u1, u2) such that u1 = U1(x1) and u2 = U2(x2). These are the utility outcomes.
In terms of physical outcomes, a bargaining situation can be characterized by its physical feasible set F* consisting of all the possible allocations between person 1 and person 2. Within F* there is a physical conflict point c* = (c1*, c2*) whose components are the payoffs, in physical units, to the two players when no agreement is reached.
In terms of utility outcomes there is a feasible set F of the possible utilities accruing to the two players from the different possible physical allocations. There is also a conflict point that can be stated in terms of the physical conflict point: c = (c1, c2) such that c1 = U1(c1*) and c2 = U2(c2*).
No essential information is lost by basing the analysis of bargaining on the possible utility outcomes defined by F and c.
1. Individual Rationality: A rational bargainer will not agree to a utility payoff smaller than her conflict payoff.
2. Joint Rationality: Two rational players will not agree to a particular utility outcome if in the feasible set F there is another point in F yielding higher payoffs for both of them. The outcome to be agreed upon is Pareto Optimal.
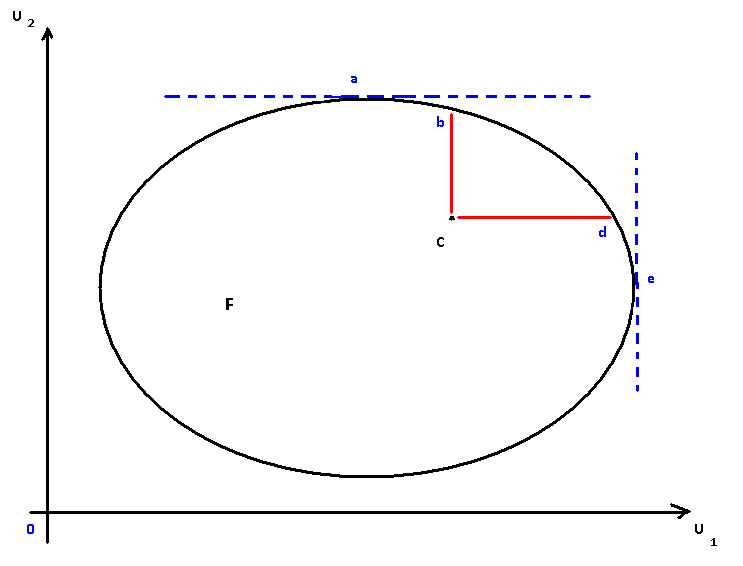
In the following figure the area F is the feasible set and c is the conflict point.
The triangular shape bcd with the two red legs is the set of all points satisfying the postulate of individual rationality.
The arc or boundary abde is the set of Pareto optimal points that satisfy joint rationality.
The intersection between the triangular shape bcd and the boundary abde is the arc bd. It is this arc, bd, that satisfies both individual and joint rationality. Depending on where you look in the historical record this arc has been variously called the possible final settlements, the range of practicable bargains, or the negotiation set.
Let's call b person 1's concession limit, and correspondingly d is person 2's concession limit.
Prior to the advent of game theory, neoclassical economic theory could only tell us that the two players would wind up somewhere on the arc bd. Economics was not able to say anything more about the bargaining outcome nor how the players arrived at a particular outcome. In this respect there was only a weak bargaining theory.
Among the many contributions to economics and game theory made by von Neumann and Morgentstern was their concept of (expected) utility which permitted a characterization of the players' attitudes toward risk. As an example of von Neumann - Morgenstern utility we might consider Tommy's utility from fish and pineapple. If he works by himself he can have, say, 1.71 fish and 4.28 pineapples. On the other hand he could bargain for more of both from Penny or Nicky. He supposes that with probability q that he will reach an agreement whereby he ends up with 1.81 fish and 4.53 fish, and with probability (1-q) he is left on the beach by himself. With these ideas in his head his expected utility is EUtommy = q*Utommy(F=1.72, P=4.28) + (1-q)*Utommy(F=1.81, P=4.53).
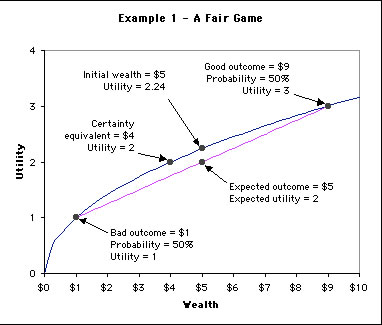
Suppose Oskar has a utility function given by 
. This is a legitimate utility function since U' > 0 and U" < 0. In other words there is diminishing marginal utlity to money. The following figure illustrates what he would accept in lieu of a fair gamble, or his willingness to buy costless insurance. Note that U(Ew) > EU(w). We know this by Jensen's Inequality.
Another, not so recent innovation, is the use of discounting to represent costly delays. Are you indifferent between receiving a dollar today and a dollar next year? The answer is NO. The promise of $1 next year is only worth (1/(1+r))($1) to you today, when r is the interest rate. Suppose the interest rate is 10%. You would be indifferent to the choice between receiving $0.91 today and $1 next year. This is because you could invest your $0.91 at the start of the year at 10% and receive $1 from the bank at the end of the year. Simlarly, the promise of a dollar at the end of two years would only be worth $0.82 since .82*1.1*1.1 = 1. This idea is important since the longer you expect it to take to reach a settlement, the less valuable that settlement is to you today. Delay in reaching a settlement is costly.
Nash's approach to the bargaining problem postulated that the solution should satisfy four axioms:
1. Efficiency: The solution is efficient if it satisfies the joint rationality assumption referred to earlier.
2. Symmetry: A symmetric game will have symmetric agreement point. First, a definition. A game is symmetric if interchanging the two players will not change the game. Under this defintion the set F would be symmetric around the 45o line through the origin and the conflict point lies on that line. In our figure the agreement point satisfying this axiom would be the intersection of the 45o line and the arc bd.
3. Linear invariance: Game G' can be obtained from game G by an affine transformation (order preserving) of Player 1's utility function while leaving 2's unchanged. If in game G the palyers agreed to the physical outcome (x1, x2) then in game G' they will agree to the same physical allocation, although 1's utility has been changed by the transformation. The implication of this is that not interpersonal utility comparisons are made or matter.
4. Independence of Irrelevant Alternatives: An alternative is a member of F, the set of feasible outcomes. Suppose that in the figure the boundary bd, including the line itself, is smooth as we have drawn it; in math-speak the boundary is a convex and compact set (bounded and closed). Further, suppose that the agreement point is on the boundary bd. Now create a new, smaller game that includes just a portion of bd, and the conflict point and original agreement point are members of that smaller game. Because the smaller game includes the original conflict point and the original settlement point it too will be played to the same settlement point. We conclude that the feasible outcomes, alternatives, that were trimmed away were irrelevant to the game.
Nash proved the following theorem:
Theorem 1: If the four axioms are satisfied then the agreement point of a game will be the unique utility vector 
that maximizes the Nash Product 
subject to 
and 
.
The solution can be illustrated using the figure above. Extend the horizontal and vertical red lines as though they are a new set of Euclidean axes. The solution is the tangency between a rectangular hyperbola and the the boundary bd and bounded by the red axes.
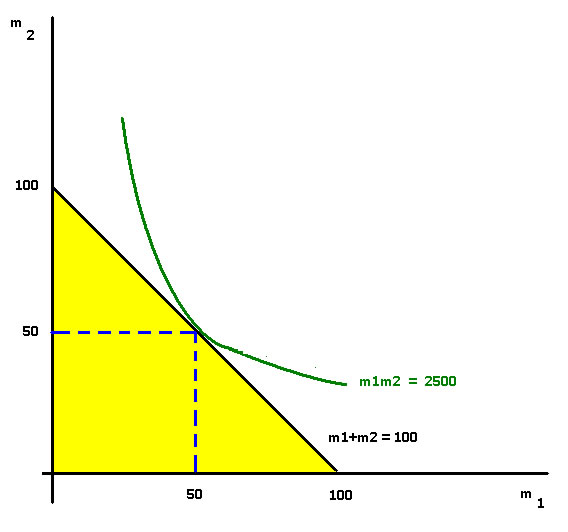
Example 1: Two individuals are bargaining over $100. If they cannot agree on the sum of money each is to receive, denoted m1 and m2, then neither of them gets any money. The feasible set consists of all the pairs such that m1 + m2 ≤100. Each player's utility is just the sum of money that each receives, i.e., u1 = m1 and u2 = m2. The conflict point is c = (0, 0). The game is symmetric. The Nash solution is to find the tangency between the line m1 + m2 = 100 and the hyperbola H=m1m2. The solution is m1 = m2= 50. Since the solution lies on the boundary of a convex and compact set it is Pareto optimal. The solution satisifies symmetry. The solution is also invariant to linear transformations of utility.
Example 2: Esther Tate has listed her house at $120,000. Her reservation price is $100,000, since she feels that at any price below $100,000 she would be better off just keeping the house. Bob Beyer comes to look at the house and decides that her would pay as much as $120,000 for it; this is his reservation price. Nonetheless, Bob would be better off if he paid less than his reservation price. Following the same argument as that in Example 1, the Esther and Bob should share the $20,000 gain equally.
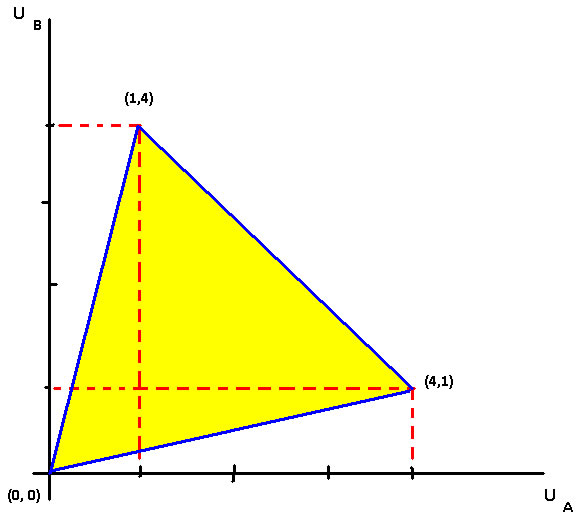
Example 3: Frank Gifford and Kathy are trying to decide whether they should go to a football game or to the opera. The set of outcomes is given by F = {go to football, go to the opera, disagreement. If they go to the football game then Frank's utility is UG = 4 and Kathy's utility is UK = 1. If they go to the opera then their utilities are reversed. If they disagree then they each get zero utility; UG = UK = 0. This problem is also solved using the Nash Product. Unfortunately, there are two solutions to this bargaining problem: Either both go to the football game or both go to the opera. At this point Gifford and Kathy may decide to flip a coin to see where they should go. Notice that at this point there is an element of cooperation, since they have mutually decided to avoid the conflict point. Should they use a fair coin? Suppose the coin has a football on one side and opera on the other. The probability that the coin lands with football showing is 'p.' Gifford's expected utility EUG = 4p + 1(1-p) and Kathy's expected utility from the coin toss is EUK = 1p + 4(1-p). Applying the Nash Product in expected utilities we get π = (3p+1)(4-3p) = -9p2 + 9p + 4. The p that maximizes this function is 1/2. The process of having Gifford and Kathy toss a coin has the effect of extending the set of outcomes to include joint randomization (also known as correlated utilities). The 'solution' to the bargaining game is a probability distribution. [Is the use of a fair coin coincident with our earlier visit to the Battle of the Sexes as a non-cooperative game?] The set of correlated utility allocations can be represented graphically as
Does the Nash Product Always Work?
The Nash solution works for games that are symmetric in the set of feasible solutions. It works for games that are asymmetric in risk aversion and in conflict points. However, it doesn't work too well when the utility allocations are asymmetric. Bankruptcy is an example. A firm contemplates seeking bankruptcy protection when its liabilities exceed its assets. As long as the firm remains a going concern the bondholders can expect to be repaid in proportion to the size of their initial loan. When the firm becomes insolvent the creditors must argue/bargain over who gets paid and now much. If the Nash solution is used to sort things out then each creditor gets an equal share, regardless of the value outstanding of the loan they made to the firm.
Example 4: Bankruptcy - Your bank and Mac Krell have made loans to Ann Chovie who used the proceeds to buy a shrimp trawler, which she is using as collateral for the loan, on the Gulf Coast. As a result of the massive oil spill there in 2010 the Gulf shrimp industry has collapsed and her boat has lost value. Ann is now upside down in the loans. Let K (as in Kapital) be the value of the asset and D1 and D2 represent the debts secured by the boat. Bankruptcy occurs when K < D1 + D2. We'll suppose that you and Mac are both risk neutral so the utility you get from an agreement can just be reprsented by the cash each of you gets; (c1, c2). The disagreement point can be similarly represented as (0, 0); remember the linear invariance axiom. No creditor can receive more in the bankruptcy than the amount of their loan. Let's assume D1 > D2. There are two cases.
CASE 1.
Referring to figure C1, the Nash solution is applicable and each player receives K/2.
 |
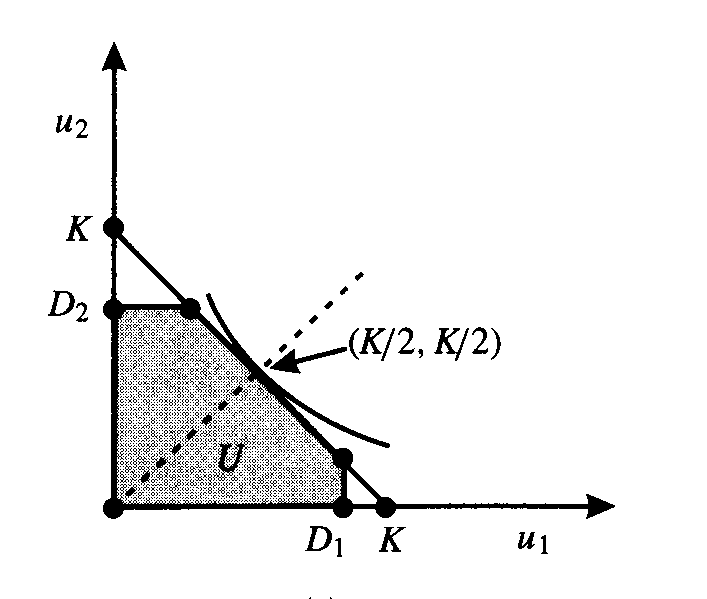CASE 2.
The relevant bargaining game is now shown in figure C2.
 |
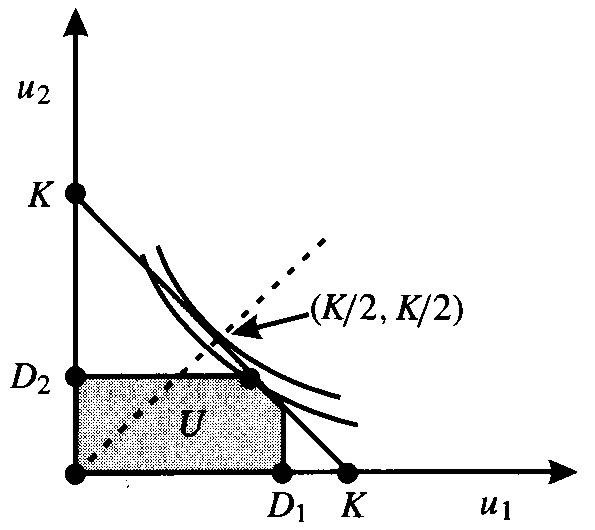The Nash solution is shown, but it would 'unfairly' give more to Mac than he is owed and you would receive less than you are owed. If the spoils of selling Ann's boat are divided proportionately to what each creditor is owed then the follwoing pair of equations would be solved.
To see how it works suppose K=100, D1 = 100, D2 = 50. Find the Nash solution and the proposed rule.
An alternative to the symmetry requirement might be an idea known as monoticity.
Monotinicity: A solution rule is said to be monotone if for any bargaining game that consists of a feasible set of utility outcomes (F), the players' utility functions, and disagreement points and any subset of the feasible solutions ( 
), the solution set of the original game dominates the solution set on T.
The Nash solution rule does not satisfy monotinicity. Take a look at Figure Monotone. The right panel is the original game and the left hand panel is a subset of that game. In the whole game player one gets less than he would get under the subset T, so he cannot be better off.
 |
 |
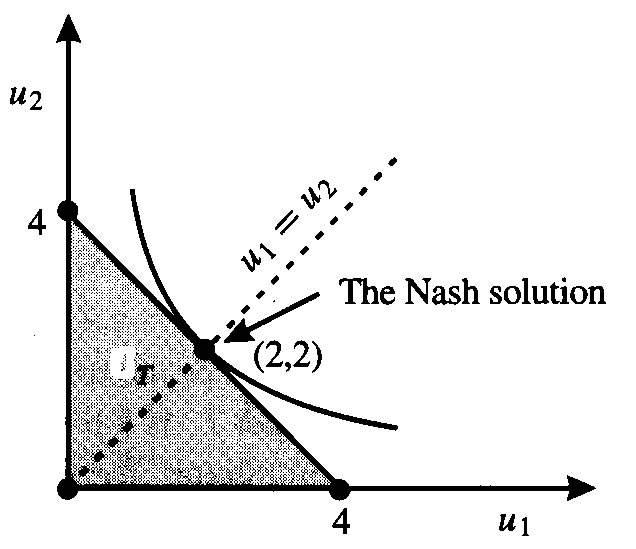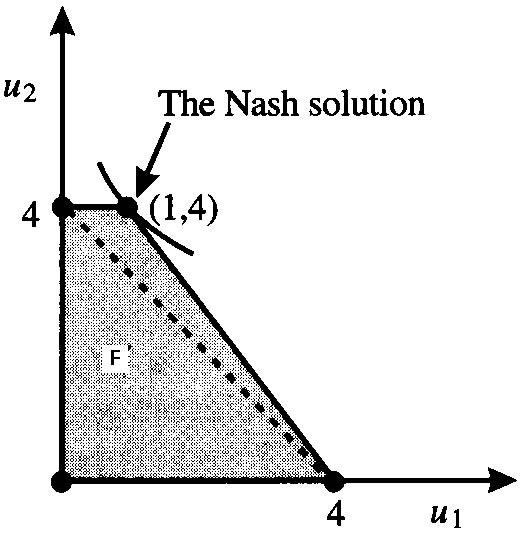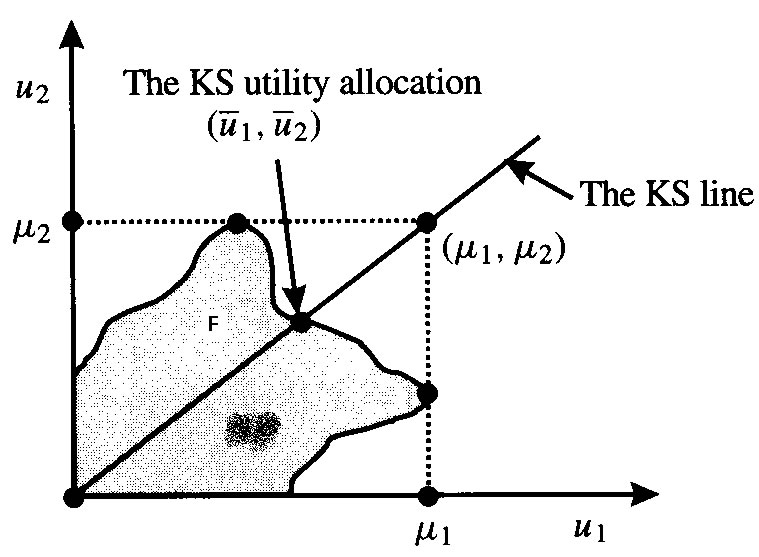
To solve the problem of asymmetries we use the Kalai-Smorodinsky rule. To understand the rule a recipe is proposed.
Kalai-Smorodinsky Recipe
1. Under the feasible set of utility allocation, find the maximum possible utility obtainable by each player. Call these 
.
2. Draw a ray
..3. The solution is the most northeastern point on the drawn ray that is still a member of the feasible set.
To understand what was done see Figure KS.
 |
 |
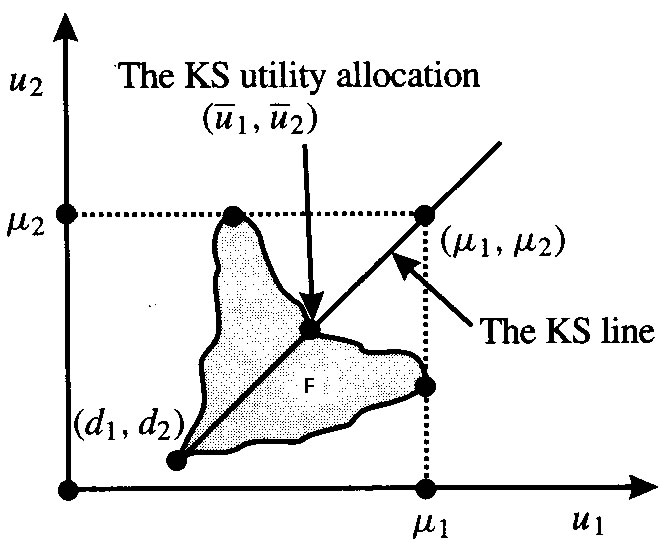The Kalai-Smorodinsky Soultion Rule is independent of linear transformations, like Nash. The KS solution set consists of Pareto optimal allocations, like Nash. Kalai-Smorodinsky is not independent of irrelevant alternatives. When a game is symmetric in its feasible utility allocations the Nash and K-S solutions are the same.
Example 5 A Wage Bargaining Game
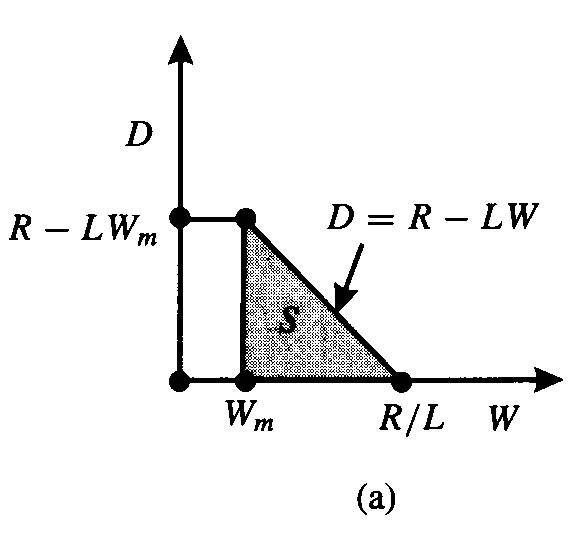
Buck's Bolts is entering into wage negotiations with the Amalgamted Brotherhood of Bolt Adjusters (ABBA). Let Wm be the wage that the workers will get if the negotiations break down. If negotiations break down then the firm shuts down and earns a profit of zero. Let L be the size of the union membership. Buck's Bolts sells its output at a price of p in a perfectly competitive market. The firm's output is a function of the amount of labor emplyed, f(L). The firm pays a wage W. Putting things together we can write the firm's profit as
Profit = pf(L)-LW
Management pays a dividend D to the shareholders from the profits.
We'll let the firm be player 1 and the union be player 2. Also, for notational convenience, let R = pf(L). The bargaining game is given by d1 = 0, d2 = LWm, u1(W,D) = pf(L)-LW-D, and u2(W)=LW. We know that the eventual wage will not be below Wm, nor will it be greater than R/L. Additionally, the dividend must be no less than zero and it can be no more than the operating profit of the firm, R-LW. The bargaining set defined by these requirements is shown in the left panel of Figure Union. It is drawn in the Dividend - Wage plane. In the right panel the set of utility allocations is shown.
 |
 |
 |
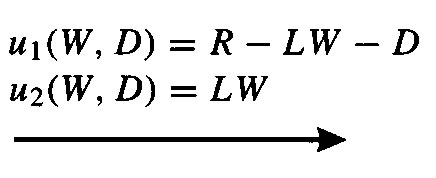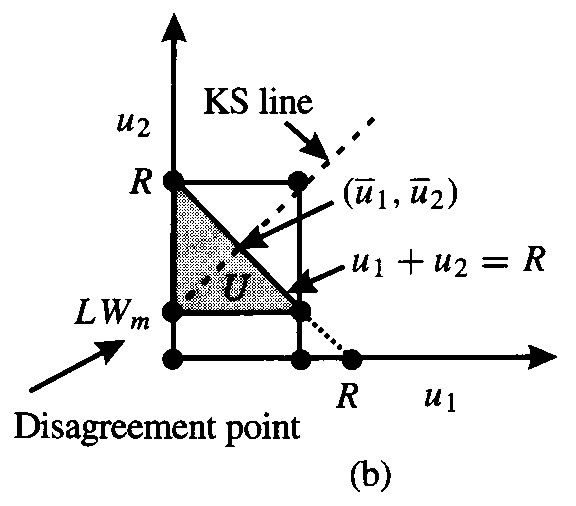The slope of the KS line must be one since it must go through the disagreement point and the point whose coordiantes are the maximum utilities for the players. Can you show that
the utilities at the solution are 
and
? Can you determine the wage paid and the dividend to be paid?
We saw above that the Pareto Optimal allocation may not be unique; we needed to impose other criteria in order to solve 2 person bargaining problems. Additionally, we still need to generalize cooperative games to more than two participants. There are a number of concepts, including several with interesting results; but here attention will be limited to one. It is the Core, and it builds on the Pareto Optimal solution set, allowing these two problems to solve one another via "competition."
A coalition is a subset of the economy's consumers.
The core is the set of feasible allocations that cannot be improved upon by a subset (a coalition) of the economy's consumers.The idea of the core already appeared in the writings of Edgeworth (1881), at the time referred to as the contract curve. Even if von Neumann and Morgenstern considered it an interesting concept, they only worked with zero-sum games where the core is always empty.
A coalition is said to improve upon or block a feasible allocation if the members of that coalition are better off under another feasible allocation that is identical to the first except that every member of the coalition has a different consumption bundle that is part of an aggregate consumption bundle that can be constructed from publicly available technology and the initial endowments of each consumer in the coalition.
An allocation is said to have the core property if there is no coalition that can improve upon it. The core is the set of all feasible allocations with the core property.
Utility is transferable if one player can losslessly transfer part of her utility to another player. Such transfers are possible if the players have a common currency that is valued equally by all. Note that being able to transfer cash payoffs does not imply that utility is transferable: wealthy and poor players may derive a different utility from the same amount of money.
In cooperative games with transferable utility no individual payoffs are given. Instead, the characteristic function determines the payoff of each coalition. The standard assumption is that the empty coalition obtains a payoff of 0. The origin of this game form is to be found in the seminal book of von Neumann and Morgenstern who, when studying coalitional normal form games, assumed that when a coalition C forms, it plays against the complementary coalition (
) as if they were playing a 2-player game. The equilibrium payoff of C is characteristic. Now there are different models to derive coalitional values from normal form games, but not all games in characteristic function form can be derived from normal form games.
In cooperative games players act efficiently when they form a single coalition, the grand coalition. The focus of the game is to find acceptable distributions of the payoff of the grand coalition. Distributions where a player receives less than she could obtain on her own, without cooperating with anyone else, are unacceptable - a condition known as individual rationality. Imputations are distributions that are efficient and are individually rational.
Consider a group of n miners, who have discovered large bars of gold. If two miners can carry one piece of gold, then the payoff of a coalition S is
If there are more than two miners and there is an even number of miners, then the core consists of the single payoff where each miner gets 1/2 of a bar of gold. Each and every 2 person partnership/coalition is core.
If there is an odd number of miners, then the core is empty. Why?
There are 3 miners, A, B, and C. There are a large number of gold bars in the mine, the miners can make one trip into and out of the mine. It still takes two miners to carry out a bar of gold. Suppose A and B form a coalition and choose to split all the gold between them, then C could offer A a split that is not 50/50 as an attempt to induce A to change his coalition partner. In order for this to be an improvement, C would be getting some non-zero amount less than 1/2 and A would be getting the rest, meaning that B could always team up with C to split 50/50 again. So since any payout besides (1/2, 1/2, 0) leaves 2 miners that are getting less than 1/2 (and would thus benefit from a 50/50 split), and the payout of (1/2, 1/2, 0) can be improved by the miner getting 0 offering a non-50/50 split to one of the others, no coalition and payout is core.
Mrs A and Mrs B are knitting gloves. The gloves are one-size-fits-all, and two gloves make a pair that they sell for €5. They have each made 3 gloves. How will the knitters share the proceeds from the sale? The problem can be described by a characteristic function form game with the following characteristic function: Each lady has 3 gloves, that is 1 pair with a market value of €5. Together, they have 6 gloves or 3 pair, having a market value of €15. Since the singleton coalitions (consisting of a single lady) are the only non-trivial coalitions of the game, all possible distributions of this sum belong to the core, provided both ladies get at least €5, the amount they can achieve on their own. For instance (7.5, 7.5) belongs to the core, but so do (5, 10) and (9, 6), to name just two.
The example can be generalised. If Mrs Carlson and Mrs Delacroix are also part of the club and still each lady has made 3 gloves, now the total to distribute is 12 gloves, six pairs, that is, €30. At the same time one of the ladies, on her own can still get only €5. Thus imputations share €30, such that no-one gets less than €5. The following are all imputations: (7.5, 7.5, 7.5, 7.5), (10, 5, 10, 5), (5, 15, 5, 5) or (7, 5, 9, 9).
For the moment ignore shoe sizes: a pair consists of a left and a right shoe, which can then be sold for €10 per pair. Consider a game with 2001 players: 1000 of them have 1 left shoe, 1001 have 1 right shoe. The core of this game is somewhat surprising: it consists of a single imputation that gives €10 to those having a (scarce) left shoe, and 0 to those owning an (oversupplied) right shoe.
We verify that this is indeed the case. Observe that any pair having a left and a right shoe can form a coalition and sell their pair for €10, so any pair getting less than that will block the imputation. So if an imputation is in the core, we can write down left-right pairs and any of these pairs will get at least 10, in fact, exactly 10, since in the end we can only sell 1000 pairs, making the total budget equal to 10000. This leaves a right-shoe owner with 0 payment. Now go through the pairs: if there is a left-shoe owner who has less than 10, say 8, then it can join this poor right shoe player, sell their pair of shoes, give him the poor right shoe holder 1, and keep 9 to herself. This way both are better off. For stability such a left-shoe owner cannot exist: all left shoe owners already get 10.
The message remains the same, even if we increase the numbers as long as left shoes are scarcer. The core has been criticized for being so extremely sensitive to oversupply of one type of player.