Sequential Games with Uncertain Outcome:

  Involuntary Unemployment  

In the usual competitive labor market model that underlies much of macroeconomic theory it is not possible to have an equilibrium with involuntary unemployment.  How can there be an equilibrium if firms will not hire a willing and able worker at the market wage rate?

In the Keynesian model wages are assumed to be sticky downward even when there is an excess supply of labor.  Since this flies in the face of classical economic beliefs there has to be some mechanism to generate this stickiness.  Possible explanations include long term contracts and confusion between real and money wage rates.  Either of these explanations is problematic.  If there are many employers in many industries then contracts would be staggered and in the aggregate there would always be expiring contracts.  In the other explanation rational economic agents would soon learn not to be fooled by money wages.

As an alternative explanation suppose that labor is not homogeneous in the effort brought to the workplace.  In this modification workers can shirk at some risk of dismissal and employers can monitor the employees at some financial cost.  In this model labor productivity is a function of both the firm's technology and worker effort.  Also, the firm's total costs are a function of input costs, output and monitoring.

Proposition: The market clearing wage, w*, is not a stable equilibrium.  If all firms pay w* then some firm could do better by offering w*+¢.  The higher wage makes it more costly for the firm's workers to shirk and risk losing their job.  Higher productivity would more than offset the higher wage.  Workers who are out of work are not hired at a wage below w* because firms expect them to be shirkers!

The workers at Hudson.com, an online retailer, are very versatile; they take orders, fulfill orders, manage and clean the warehouse, do a bit of programming, etc.  Because of their many tasks it is possible for them to sneak off to the bathroom for some roll-time, play games on their palm pilot, or generally slack off.  Hence the effort adjusted labor force is

L_s = L·S

where L is the number of workers and S is the % of time NOT spent shirking; .  The firm's revenue is R = R(L_s) = ln(1+L_s).  The advantage of the natural log specification of revenue is that it has the following properties:

R(0) = 0,  .  

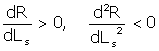Since management cannot directly observe L_s, the firm's costs are C = W·L.  The firm's efficiency wage is W_s = W/S, where W is the posted wage.  Profits are V(W, L, S) = ln(1+L_s) - W·L.

Like the rest of us, the employees of Hudson get satisfaction, or utility, from income and leisure. 

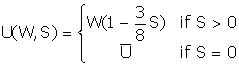
When S=0 it means that all of the employee's time is spent shirking.  That is, she is not working.  The person that is not working still has some satisfaction from consuming all of her time as leisure.  In that base case, when all time is used for leisure, we say that the person has some level of satisfaction equal to her reservation utility, denoted .  In the tree diagram of the extensive form of the game the reservation utility is called U-bar since I can't put "symbols" in the software that creates the tree.

Hudson is able to detect and dismiss shirkers with probability .  

We are now ready to model the game tree confronting a hypothetical employee named Leland.

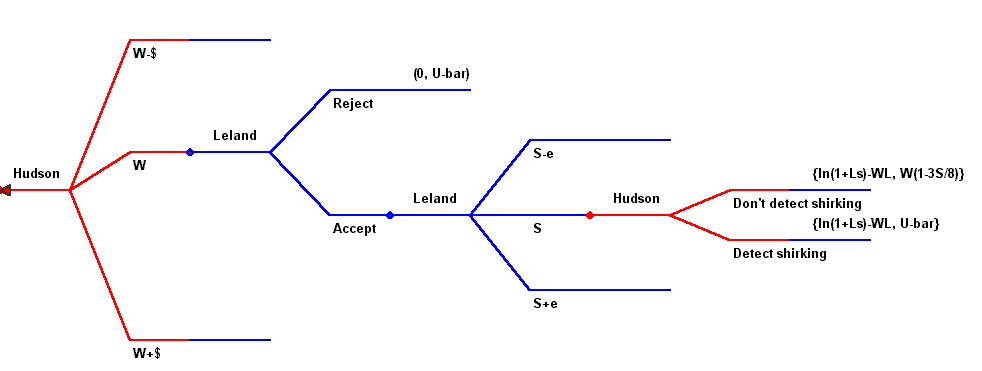
Using backward induction, Leland wants to maximize his expected utility.  That is, if he were able to play the game repeatedly, he would want to calculate his long run payoff from a given level of effort S.  By substitution we can write expected utility as

To find the maximum take the derivative with respect to S, set the result equal to zero, and solve for S*.

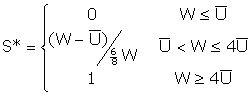
Assuming that the reservation utility is 1, the graph of Leland's work effort looks like:

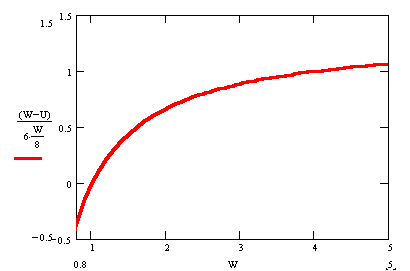
The conclusion to be reached at this point is that Leland will accept the job offer if and only if the offered wage is above his reservation utility.  From the graph we can see that if Hudson offers a wage equal to Leland's reservation utility then Leland will come to the job site, but do no work!
 Therefore, any wage below is a dominated strategy.  Any wage above 4is also dominated since Leland cannot make an effort of more than 100%, unless he happens to be an American professional athlete, and we all know that they put out 110% effort.

To find the wage that the firm will offer, put S* into Hudson's profit function.

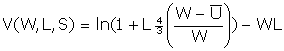
The firm maximizes its profits by its choice of the wage offer, W, and by its choice of the number of workers to hire, L.  To find the maximum of V(.) we differentiate with respect to W and L, set the two derivatives equal to zero, and solve the pair of equations for W and L.

(i)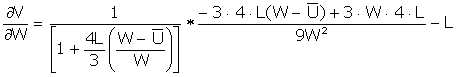     

or    

(ii)     -W

or    

We can rearrange (i) as

And (ii) can be rearranged as

Setting the left hand sides equal to one another we can solve for the wage offer.

The firm should pay its workers a wage equal to twice Leland's reservation utility. The firm is paying a wage greater than necessary to induce Leland to come to work for it.  Hudson does this knowing that Leland's increased effort will more than offset the higher wage paid.

We can plug W* into Leland's effort function to see how hard he works:

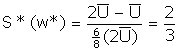
Now plug W* into (ii) in order to find the number of workers that Hudson ought to hire.

if the reservation utility is less than 1/3.  If reservation utility is greater than 1/3 then Hudson will not hire anyone.  

Going back to the optimal effort to be made by Leland,

.  

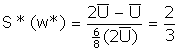With this effort level Leland will be shirking one third of the time.  This is due to the fact that monitoring is costly for the firm and additional income has diminishing marginal utility for Leland.  With this amount of shirking Hudson will pay Leland an efficiency wage of

At the optimal wage and effort levels Leland's expected utility (wage) from work and leisure (shirking) is

In working for Hudson Leland is earning an expected wage that is 1/3 more than he could have earned in his next best alternative.  But the contracted wage being paid to workers is   .  Why doesn't Leland seek a higher wage than his expected wage?  Why doesn't Hudson offer a wage below ?  In short, why don't they get together and find an agreement between , Leland's expected wage, and , the contractual wage? 

Suppose Leland finds that he isn't one of the lucky few to land a job.  Leland should be willing to work for a wage just slightly above his reservation wage. Unfortunately Leland cannot credibly commit to a work effort of 2/3 at the lower wage because Hudson rationally expects him to put in less effort.  In short, if Leland doesn't have a job he just has to join the queue and wait until enough shirkers have been fired that his name rises to the top and he works for .

Suppose Leland is working.  He gives some thought to being laid off for shirking and offers to work for a contracted wage of less than W* in return for a guarantee of no layoff.  The problem is that Leland cannot credibly commit to a higher work effort, necessary to justify the higher wage, that would lead to an expected wage greater than  .

So far we have treated as exogenous.  To complete our consideration of involuntary unemployment we need to create a market for labor and see if people like Leland are out of work.  What are Leland's alternatives to working for Hudson?  Suppose that there are many firms like Hudson.  To keep things simple we will even go so far as to say that they are identical in every respect.  Each of these firms makes their employment and wage decisions in the same way as Hudson and independently of one another.  Therefore all of the firms pay the same expected wage to each worker.  If this is a market clearing wage then any worker is able to find alternative work as soon as she is fired.  But if this is the case, then the equilibrium wage that we found above should also be the same as the reservation wage.  Hmmm. There is a contradiction here.  The reservation wage we saw to be and the expected wage is .  Therefore, the equilibrium wage is not the same as the market clearing (reservation) wage!  There must be some unemployment.

Since there is some unemployment each firm faces an excess supply of labor.  The available jobs are rationed on a first come, first served basis.  In any market period the firm catches one third of its labor force shirking and fires them and these workers go to the end of the queue. The firm, say Hudson, can then enter the market and hire replacements.  The length of the unemployment queue is what makes being fired painful.  The longer the queue, the lower the reservation wage will be.  

Let L_T be the total number of people in the workforce.  If there are n firms each employing L* workers then the number of unemployed will be L_T - nL*. Each period the firm catches one third of its employees shirking and fires them and immediately replaces them with people from the unemployment queue.  This leads us to conclude that there will be new hires each period.  If we divide the number of unemployed by the number of new hires each period we can find the number of periods a worker will remain unemployed when fired.

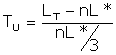
Substituting in for L*

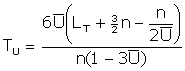is the length of time a worker will remain unemployed after being fired.  

On the other side we have to consider the reservation wage/utility of the worker as a function of the length of time she is unemployed. To derive such a function we need to consider a dynamic model.  In the dynamic model each worker considers the present value of expected wages in future periods.  In addition to the probability of being fired, such a function would be a function of the duration of unemployment.  Without trying to set up and solve such a problem in dynamic programming we will just suppose that it obeys the following

Plotting T_u(·) and U(·) allows us to solve for the equilibrium reservation wage and the equilibrium duration of unemployment.  In any event the important message is that there is involuntary unemployment. 

Further remarks

1.  If we interpret reservation utility as unemployment benefits, then an increase in unemployment benefits will increase the equilibrium level of unemployment.  This seems to be common sense.  It is "better to play for nothing than to work for nothing".

2. If there is a decrease in the demand  for labor (due to a macroeconomic shock), then the wage rate will fall and there will be a higher level of unemployment.

3. There may be interventions in the job market that will make workers better off.  Wage subsidies can result in higher levels of employment.  Unemployment insurance supplied by the government will result in making the spell of unemployment less difficult.  To the extent that a turnover tax reduces the flow of job vacancies, it makes the threat of firing more severe

4. Firms that find shirking to be especially costly will offer higher wages than other firms do.