|
|
||
|
|
International Trade |
|
|
|
||
|
|
International Trade |
|
The standard model of international trade in economic theory is the Hecksher-Ohlin-Samuelson Model: Two goods (corn and steel) are produced in competitively organized industries in each of two countries (Erehwon and Xanadu).
The two countries are both producing corn at the same constant marginal cost of $1/bushel; they have the same resource endowment and the same technology. The firm producing corn in Xanadu is called Rosebud, the firm in Erehwon is called Orez. They also have the same taste for corn; their demand curves are
![]() for Erehwon and
for Erehwon and
![]() for Xanadu.
for Xanadu.
 Initially
there is an impassable mountain between the two countries. Therefore each
firm earns its profit domestically. For Orez in the country of Erehwon
their profit is
Initially
there is an impassable mountain between the two countries. Therefore each
firm earns its profit domestically. For Orez in the country of Erehwon
their profit is
![]()
For Rosebud in the country of Xanadu their profit is
![]()
Since the countries and firms are identical and there is no trade we can derive the profit maximizing output and price for one firm and know that it will be the same for the other. To find the profit maximizing output for Orez we differentiate their profit function with respect to QE, set the result equal to zero and solve for QE, then plug the result back into the demand curve to find the appropriate price. Profit can be found by plugging the solution for quantity into the firm's profit function.
![]()
QE = 20
Notice that the total revenue received from the production and sale of 19 bushels is $68.875 and from 20 bushels it is $70. The gain in revenue, or marginal revenue, is $1.125.
![]()
![]()
 |
One day Paul Bunyan comes upon the scene and espies the mountain between the two countries. As a student of economics he concludes that the residents of Erehwon and Xanadu would be much better off if there was free trade between them. Therefore he resolves to shovel away the bulk of the mountain. Once he is done the only impediment to trade is distance. Without the mountain it costs $1 to ship a bushel of corn from one country to the other. Will there be trade in corn between the two countries? |  |
Suppose Orez produces another bushel of corn and ships it from Erehwon to Xanadu. It costs them $1 to produce the bushel and $1 to ship it. Initially they receive $3.50 when they sell that first bushel abroad. So their marginal profit from the bushel produced and sold abroad is $2.50. Of course if both firms do this then prices will be driven down. Let us formalize these ideas. Orez can sell its corn in either Erehwon or Xanadu. Similarly, Rosebud can sell its corn in either location. Therefore, Orez's profit depends on what both firms are selling in both markets.
![]()
Similarly, Rosebud's profit depends on the quantity offered for sale by both firms in both markets.
![]()
Making the obvious substitutions
![]()
![]()
Differentiate
![]() with respect to
with respect to
![]() and with respect to
and with respect to
![]() , then set the results to zero. For Rosebud differentiate
, then set the results to zero. For Rosebud differentiate
![]() with respect to
with respect to
![]() and with respect to
and with respect to ![]() , then set the result to zero.
, then set the result to zero.
(1)
![]()
(2)
![]()
(3)
![]()
(4)
![]()
There are now four equations in four unknowns. But we are interested in the corn market in each country, so we only need to look at the first and third equations together and the second and fourth equations. The first and third are the best response functions for the two firms in Erehwon; the second and fourth are the best response functions for the two firms in the Xanadu market. The best response functions can be plotted for each of the two markets.
| On the left are the reaction functions of Rosebud and Orez in the Erehwon market. Orez sells 16 bushels in its home market and Rosebud sells 8 bushels in Erehwon. In Xanadu, the right panel, things are reversed. Rosebud sells 16 bushels in its domestic market and Orez sells 8 bushels in Xanadu. Bushels of corn has increased from 20 to 24 bushels and the price per bushel has fallen from $3.5 to $3. | |
| Are consumer's better off? Are Rosebud and Orez better
off? Is society better off?
Consumer surplus is the difference between what consumer's are willing to pay, read from the demand curve, and what they have to pay in the market. Geometrically it is the trangle under the demand curve and above the going price. But we are interested in the change in consumer surplus resulting from free trade. This amount is the shaded trapezoid in the diagram. For either country this amounts to $11, a net gain. A similar idea, producer surplus, applies to the firm. Since, say Orez, operates under constant marginal cost of $1 and its shipping cost is $1, it earns 16*($3-$1) on domestic sales and another 8*($3-$2) on foreign sales for a total of $40 after trade. Before trade they earned 20*($3.50-1) = $50. So their decline in profit attributable to free trade is $10. But when we add the increase in consumer surplus and the decline in producer surplus, society still comes out $1 ahead. |
We can gather the results of this game in a table that summarizes the consequence of each firm playing its best response against its opponents choice to trade or not. If the government in each country is trying to maximize the sum of profit and consumer surplus then we can see that trade is the dominant strategy for each.
|
Outcomes in Erehwon |
|||
|
Xanadu |
|||
| No Trade | Trade | ||
| Erehwon | No Trade | P=$3.5 Q=20 Profit=50 Consumer Surplus=25 P+CS=75 |
P=$3 QEO=16, QER=8 Profit=32 Consumer Surplus=36 P+CS=68 |
| Trade | P=$3.5 QEO=20 QXO=8 Profit=50 + 8 Consumer Surplus=25 P+CS=83 |
P=$3 Q=24 Profit=40 Consumer Surplus=36 P+CS=76 |
|
It is commonly argued that it is foolhardy to subsidize exports. In effect you tax your own citizens in order to increase the consumer surplus of your trading partners. The argument usually offered in support of subsidies is that it will increase employment in the industry receiving the subsidy. To see how all of this works, let us suppose that Erehwon elects to subsidize corn exports.
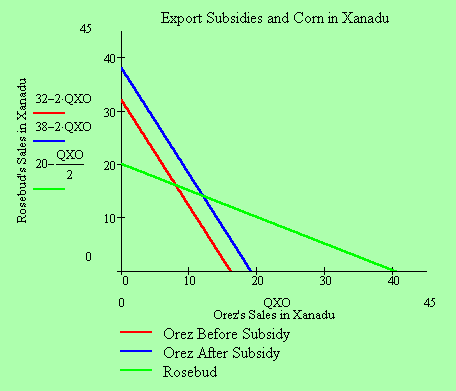 |
The government of Erehwon has decided that it will subsidize Orez's exports to Xanadu by paying them $.75 for each bushel sent overseas. This has the effect of lowering Orez's shipping costs by $.75/bushel. Their best response function in the Xanadu market changes accordingly from the red line to the blue line in the graph. Orez's exports to Xanadu increase from 8 bushels to 12 bushels, and Rosebud's domestic sales decline from 16 to 14 bushels. Overall, the residents of Xanadu now consume a total of 26 bushels at a price of $2.75 per bushel. Consumer surplus in Xanadu rises to $42.25, an increase of $6.25. At the same time Orez's profits in the Xanadu market have increased from $8 (=$3x8-$2x8) to $18 (=$2.75x12-$1.25x12), a gain of $10. But the subsidy costs the residents of Erehwon $9 in a lump sum tax, so the country's net gain is $1. |
One could ask whether or not Erehwon has chosen the subsidy that maximizes Orez's profits net of the subsidy. We have seen that the export subsidy does not change Orez's domestic behavior. Similarly, Rosebud's domestic behavior will depend on its own domestic sales and the sales of Orez in Xanadu. The objective functions with which we need to concern ourselves are
| Orez's profits from sales in Xanadu and the subsidy paid by Erehwon, to be maximized with respect to Orez's sales in Xanadu. |
| Rosebud's profits from sales in its own market, to be maximized with respect to Rosebud's sales in Xanadu. |
Doing the derivatives yields the best response functions for Orez and Rosebud in the Xanadu market, respectively:
|
|
Orez's best response function. |
|
|
Rosebud's best response function. |
Solving the best response functions simultaneously
![]()
![]()
These can then be plugged into the demand curve for
corn in Xanadu.
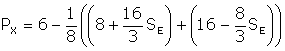
Now plug these three results back into the profit function for Orez, net of the subsidy to get
![]()
![]()
![]()
You can use the quadratic formula to solve for the roots of this equation and find that the optimal subsidy is $.75!
Suppose that both countries decide that they want to provide subsidies?
|
Consumer Surplus in a Subsidy War |
|||
| Xanadu | |||
| No Subsidy | Subsidy | ||
| Erehwon | No Subsidy | 36, 36 | 42.25, 27 |
| Subsidy | 27, 42.25 | 33.25, 33.25 | |
|
Profits in a Subsidy War |
|||
| Xanadu | |||
| No Subsidy | Subsidy | ||
| Erehwon | No Subsidy | 40, 40 | 32.5, 50 |
| Subsidy | 50, 32.5 | 42.5, 42.5 | |
Firms would like to see the government play the subsidy startegy, consumers would prefer the 'no subsidy' strategy.
|
Combined Payoff Matrix for Subsidy War |
|||
| Xanada | |||
| No Subsidy | Subsidy | ||
| Erehwon | No Subsidy | 76, 76 | 74.75, 77 |
| Subsidy | 77, 74.75 | 75.75, 75.75 | |
<Subsidy, subsidy> is the strictly dominant strategy. The firms will out in this version of the game. At the end of all this we have learned some game theory and we see that the prescription of Hecksher-Ohlin-Samuelson is not always true. What assumptions did we weaken in order to get somewhat different results? Does the use of economic theory sharpen or clarify the debate about free trade, or just serve to obscure things?
The results of the exercise, what we have learned about trade between Erehwon and Xanadu, can be summarized in a strategic form game.
|
Xanadu |
|||||||
|
No Trade |
Export with No Subsidy |
Export with Subsidy |
|||||
|
Erehwon |
No Trade | P=3.50,
Q=20 CS=25, Total Surplus=75 |
P=3.50,
Q=20 CS=25, Total Surplus=75 |
P=$3 QEO=16, QER=8 Profit=32 Consumer Surplus=36 Pr+CS=68 |
P=$3.5 QxR=20 QER=8 Profit=50+8 Consumer Surplus=25 Pr+CS=83 |
P=2.75 QEO=14 QER=12 Profit=24.50 Consumer Surplus=42.25 Pr+CS=66.75 |
P=3.50 QXR=20 QER=12 Profit=50+18 Consumer Surplus=25 Subsidy=9 Pr+CS -Subsidy=84 |
| Export with No Subsidy | P=$3.5 QEO=20 QXO=8 Profit=50+8 Consumer Surplus=25 Pr+CS=83 |
P=$3 QXO=8 QXR=16 Profit=32 Consumer Surplus=36 Pr+CS=68 |
P=$3 Q=24 Profit=40 Consumer Surplus=36 Pr+CS=76 |
P=$3 Q=24 Profit=40 Consumer Surplus=36 Pr+CS=76 |
P=2.75 QEO=14 QXO= QER=12 Consumer Surplus=42.25 Profit=32.50 Pr+CS=74.75 |
Price=3 Q= Profit=50 Consumer Surplus=27 Pr+CS -Subsidy=77 |
|
| Export with Subsidy | P=3.50 QEO=20 QXO=12 Profit=50+18 Consumer Surplus=25 Subsidy=9 Pr+CS -Subsidy=84 |
P=2.75 QXO=12 QXR=14 Profit=24.50 Consumer Surplus=42.25 Pr+CS=66.75 |
Price=3 QXO=12 QEO=16 QER=8 Profit=32+18 Consumer Surplus=27 Pr+CS -Subsidy=77 |
P=2.75 QXR=14 QXO=12 QER=8 Profit=24.50+8 CS=42.25 Pr+CS=74.75 |
P=2.75 QEO=14 QXO=12 Consumer Surplus=42.25 Profit=42.50 Pr+CS -Subsidy=75.75 |
P=2.75 QXR=14 QER=12 Consumer Surplus=42.25 Profit=42.50 Pr+CS -Subsidy=75.75 |
|
Assembling all of the results in the form of a game payoff matrix reveals that the dominant strategy for both countries is not just free trade, but free trade with export subsidies! This is quite a different outcome than we get in the Hecksher-Ohlin-Samuelson framework.
Further remarks: