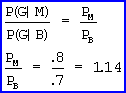
Temple University
Department of Economics
Economics 615
Probability and Descriptive Statistics
Answer Key
1. A biologist notes that the probability an insect of a particular breed is red is
.60. The probability it is winged is .50. She also notes that the probability it is red,
winged or both is .80.
a. What is the probability that a randomly selected insect is both red and winged?
P(R) = 0.6, P(W) = 0.5, P(R or W) = 0.8
P(R and W) = P(R) + P(W) - P(R or W) = .3
b. What is the probability that it is red, given that it is winged?
P(R|W) = 0.3/0.5 = 0.6
c. Are the events 'color' and 'winged' statistically independent?
Yes, they are independent.
2. John Deere buys his corn seed from two suppliers, the Maize Company and the Burpee
Company. The seeds from Maize have a germination rate of 80% and those from Burpee have a
germination rate of 70%. John buys 45% of his seed from Maize and the balance from Burpee.
Once the seed arrives on the farm he mixes the two brands together.
First construct the following table:
| G | not G | ||
| M | .36 | .09 | .45 |
| B | .385 | .165 | .55 |
| .745 | .255 |
a. Find the probability that a seed selected at random from the mixture will germinate.
.745
b. Given that a seed germinates, find the probability that it was purchased from the
Burpee Company.
P(B|G) = .385/.745 = .516
c. Once germinated, a seed from either Maize or Burpee is equally productive. Determine the price ratio of Burpee to Maize which would induce the risk neutral John to split his purchases in the fashion described.
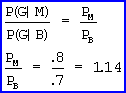
3. Monty Hall plays a game with his TV show participants to teach a valuable lesson in
probability. There are three curtains denoted A, B, and C on stage with a prize behind
each. One of the prizes is quite valuable, the other two have only nominal value. The
participant picks a curtain, although at this point it remains closed. Monty then opens
one of the remaining curtains to reveal a prize of nominal value. The participant may now
choose between the two remaining closed curtains; i.e., stick with her original choice or
switch. What strategy would you recommend? Explain.
Switch is the best strategy. Suppose that the BIG prize is behind curtain A, unbeknownst to you. You can choose any one of the three curtains.
You choose curtain A. Monty opens either one of the remaining curtains. If you switch you lose, if you hold then you win.
You choose curtain B. Monty opens curtain C since he will never open the curtain hiding the BIG prize. If you switch you win, if you hold then you lose.
You choose curtain C. Monty must open curtain B since he will never open the curtain hiding the BIG prize. If you switch you win, if you hold you lose.
You could run through the other two scenarios in which the BIG prize is behind curtain B, then behind curtain C. Because of the symmetry of the problem you don't really need to do this.
Consider the configuration of the game we have outlined. In the second stage of the game, switching results in a loss only once, but there are two ways to win if you switch. We would observe the same proportions if we worked out the other two configurations.
4. Prove
This is an application of the binomial theorem, as worked out by Bernoulli in 1660, which we use to expand polynomials of the form (a+b)2.
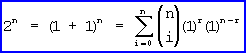
5. A line from a to b has midpoint c. A point is chosen at random on the line and marked
x. The point x is equally likely to fall in any subinterval of length h. Find the
probability that the line segments ax, bx, and ac can be combined to form a triangle.
To make this as intuitive as possible we will do it in
terms of a line of unit length. The midpoint of the line is 1/2, and we
will use the piece (0, 1/2) as the base of any potential triangle. Now
suppose we cut our original line at 3/8 so we have one piece of that length and
a second of length 5/8. If we lay the longer piece on top of the base, then
measure back 3/8 we will overlap with the base so we can make triangle. In
fact, as long as we cut the line so that the longest piece is no longer than
3/4, we can build a triangle. Hence we can cut anywhere between 1/4 and
3/4 and still be able to build a triangle. The probability of cutting
between these two numbers is 1/2, our answer.
6. A sample of 10 major symphony conductors has been selected. The number of years that
each has spent as a conductor is: 10, 7, 32, 17, 5, 23, 19, 14, 8, 2. Calculate the sample
mean, sample median, sample vaiance and sample standard deviation.