1. A biologist notes that the probability an insect of a particular breed is red is .60. The probability it is winged is .50. She also notes that the probability it is red, winged or both is .80.
a. What is the probability that a randomly selected insect is both red and winged?
b. What is the probability that it is red, given that it is winged?
c. Are the events 'color' and 'winged' statisticially independent?
2. John Deere buys his corn seed from two suppliers, the Maize Company and the Burpee Company. The seeds from Maize have a germination rate of 80% and those from Burpee have a germination rate of 70%. John buys 45% of his seed from Maize and the balance from Burpee. Once the seed arrives on the farm he mixes the two brands together.
a. Find the probability that a seed selected at random from the mixture will germinate.
b. Given that a seed germinates, find the probability that it was purchased from the Burpee Company.
c. Once germinated, a seed from either Maize or Burpee is equally productive. Determine the price ratio of Burpee to Maize which would induce the risk neutral John to split his purchases in the fashion decribed.
3. Monty Hall plays a game with his TV show participants to teach a valuable lesson in probability. There are three curtains denoted A, B, and C on stage with a prize behind each. One of the prizes is quite valuable, the other two have only nominal value. The participant picks a curtain, although at this point it remains closed. Monty then opens one of the remaining curtains to reveal a prize of nominal value. The participant may now choose between the two remaining closed curtains; i.e., stick with her original choice or switch. What strategy would you recommend? Explain.
4. Prove
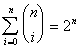
5. A line from a to b has midpoint c. A point is chosen at random on the line and marked x. The point x is equally likely to fall in any subinterval of length h. Find the probability that the line segments ax, bx, and ac can be combined to form a triangle.
6. A sample of 10 major symphony conductors has been selected. The number of years that each has spent as a conductor is: 10, 7, 32, 17, 5, 23, 19, 14, 8, 2. Calcualte the sample mean, sample median, sample vaiance and sample standard deviation.