RV's and Distributions Hwk

Economics 615
Econometrics 1

RV's and Distributions, Hwk 1

The probability distribution for the roll of two dice is

X	2	3	4	5	6	7	8	9	10	11	12
P(X)	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

You can derive this easily from enumerating the 36 possible outcomes on the throw of two dice.

The probability of winning on the first toss of the dice is P(7 or 11)=8/36, the probability of losing is P(2,3,12)=4/36, and the probability of continuing play is then 1-8/36-4/36=24/36. From this we can see that if p is our probability of winning and q is our probability of losing, then our probability of continuing to roll is 1-p-q. The probability of a win in the second stage is p. The probability of rolling on to the third stage is p(1-p-q). The probability of rolling on to the fourth stage is p(1-p-q)². We could go on and on in this fashion, but what we see is that the probability of an eventual win is

This applies to each number that we might roll as our point. Suppose your point is three. The p=2/36 and q=6/36 so the probability of a win when three is the point is (2/36)(2/8). Doing this for each of the six possible points, adding them up, then adding in the probability of a win on the very first roll will provide the probability of winning: 0.49

If you bet a dollar to play and receive $1.04 when you win, then the expected payoff is $0.

2. Find the mode.

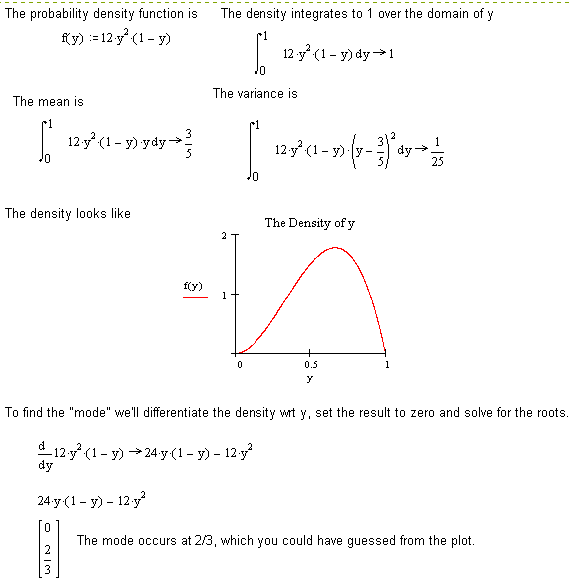
3. This is pretty straightforward.

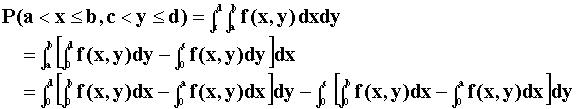
The last step is obvious.

Another way to think of the problem is with the following Venn-like diagram:

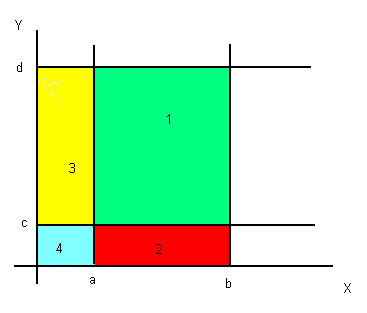
P(a<x<b, c<y<d) = green box 1. Alternatively that probability can be constructed by noting P(x<b and y<d) = Boxes 1+2+3+4, P(x<a and y<c) = Box 4, P(x<b and y<c) = Boxes 2+4, and so on. Now combine the different probabilities to get the desired result.

4. Show that Y₁+Y₂ and Y₁-Y₂ are uncorrelated.

Cov(Y₁+Y₂, Y₁-Y₂)=E{(Y₁+Y₂-E Y₁-E Y₂)( Y₁-Y₂-E Y₁+E Y₂)}

=E{((Y₁- E Y₁)+( Y₂- E Y₂))(( Y₁- E Y₁)-( Y₂- E Y₂))}

If you expand the product in square brackets you will get the difference between two variances, that were to assumed to be equal.

5. The best way to proceed is by first constructing a table:

		Y
			-1	0	2	3	4
X	-1		1/6	0	0	1/6	0	1/3
	0		0	1/6	0	0	1/6	1/3
	1		0	1/6	1/6	0	0	1/3
			1/6	2/6	1/6	1/6	1/6	1

E(Y|x=-1)=1, E(Y|x=0)=2, E(Y|x=1)=1

E(XY|x=-1)=-1, E(XY|x=0)=0, E(XY|x=1)=1

E(X)=0, E(Y)=4/3 (note that this is the sum of the expected values in a.), E(XY)=0.

No, they are not independent since the product of the marginals is not equal to the intersection. Or, the expected value of Y is contingent on x.

Corr(X,Y)=E(X-EY)(Y-EY)=EXY-EXEY=0 so they are uncorrelated.

6.a. This is an interesting portfolio construction problem. As you work on this keep the recent bailout of Long Term Capital in mind.

Expand the sums, then the expectations are more obvious.

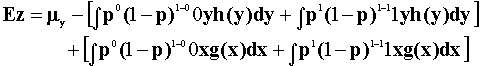
From the square bracket terms we get a weighted average of the mean of y and mean of x.

From the answer to a. you can see that

since the mean of y is greater than the mean of x we know that the mean of z is less than the mean of y.

Find the variance of the portfolio.

Collect, rearrange, expand the square and take expectations as in part a. to get

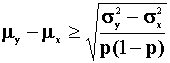
The requisite inequality can be found by rearranging part c. to get:

There is a more transparent way to do problem 6. Begin by observing that W,X, and Y are independent, EW=p, Var(W) = EW²-(EW)²=p(1-p), .

EZ=EWX+E(1-W)Y=EWEX+(1-EW)EY. The final step is obvious.

Same as above.

Complete the square, expand the terms, use the independence assumption and recall that EW² = p.

d. Same as above.

		Y
			-1	0	2	3	4
X	-1		1/6	0	0	1/6	0	1/3
	0		0	1/6	0	0	1/6	1/3
	1		0	1/6	1/6	0	0	1/3
			1/6	2/6	1/6	1/6	1/6	1

		Y
			-1	0	2	3	4
X	-1		1/6	0	0	1/6	0	1/3
	0		0	1/6	0	0	1/6	1/3
	1		0	1/6	1/6	0	0	1/3
			1/6	2/6	1/6	1/6	1/6	1

		Y
			-1	0	2	3	4
X	-1		1/6	0	0	1/6	0	1/3
	0		0	1/6	0	0	1/6	1/3
	1		0	1/6	1/6	0	0	1/3
			1/6	2/6	1/6	1/6	1/6	1