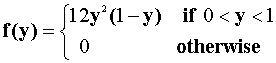
Temple University
Department of Economics

Economics 615

Homework 1

Probability, Random Variables and Distributions

1. The game of craps is played as follows.   A player tosses two dice until the player either wins or loses.  The player wins on the first toss if the player gets a total of 7 or 11; the player loses if the total is 2, 3 or 12.  If the player gets any other total on the first toss, then that total is called the point.  The player then tosses the dice repeatedly until either a total of 7 or the point is obtained.   The player wins if the player gets the point and loses if the player gets a 7.   What is the player's probability of winning?

2.  Let Y be a random variable with probability density function f(y).  The mode of of the distribution of Y, assuming it exists and is unique, is that value of y that maximizes f(y).  Find the mode in the following case.

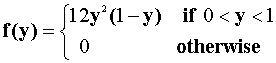
3. Let F(x,y) be the distribution function of X and Y.  Show that

for all real numbers a>b, c<d.

4.  Let Y₁ and Y₂ be random variables with the same variance.  Show that Y₁+Y₂ and Y₁-Y₂ are uncorrelated.

5.  Suppose f(y|x) is defined by

f(y=-1|x=-1) = f(y=3|x=-1) = ½

f(y=0|x=0) = f(y=4|x=0) = ½

f(y=0|x=1) = f(y=2|x=1) = ½

and that f(x=-1) = f(x=0) = f(x=1) = 1/3

5.a. Find E(Y|x=-1), E(Y|x=0), and E(Y|x=1)
5.b. Find E(XY|x=-1), E(XY|x=0), and E(XY|x=1)
5.c. Find E(X), E(Y) and E(XY)
5.d. Is Y independent of X?
5.e. Are X and Y uncorrelated?

6. Consider the random variables X and Y with means and , variances  and , and covarinace .   Suppose Y is the return on a stock and X is the return on a bond such that >and >.  Finally let W be a Bernoulli random variable distributed independently of X and Y, where P(W=1)=p and P(W=0)=1-p, and 0<p<1.  Consider the random portfolio Z=WX+(1-W)Y.

6.a. Find .

6.b. Which is larger or  ?

6.c. Find .

6.d. How large must -be in order for >?