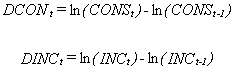Temple University
Department of Economics

Econometrics II
Multivariate Time Series

From the web site you will fetch a file named C&IVAR.DAT. A listing of the file is attached. The first column is the year, the second is the quarter, the third is consumption spending and the fourth is income. The data are in billions of dollars, seasonally adjusted.

DO NOT INCLUDE A LISTING OF THE DATA WHEN YOU TURN IN YOUR HOMEWORK!

1. Plot the data on consumption and income. What do you see?

2. Take natural logs then first difference each series. That is, construct

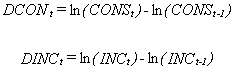
Plot the two new series. What do you see?

3. We posit a structural relationship between consumption and income. Suppose that current consumption (C) depends on current income (Y) and, due to habit formation, lagged consumption. One can write

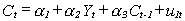
It is also plausible that current income depends on lagged income, by inertia, and lagged consumption, by the multiplier principle. One can write

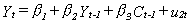
a. Using both the original series and the transformed series, estimate the model parameters by OLS.
i. Do you foresee any problems at the time of estimation? Make any necessary corrections.
ii. Do the two sets of coefficient estimates have the same interpretation, apart from any estimation problems you may have identified?
iii. Is one set of parameter estimates preferred to the other? Why?

4. Rewrite the model in its reduced form. Be sure to indicate the relationship between the reduced form coefficients and structural coefficients.

5. Estimate the coefficients of the reduced form model using both the original and transformed series. Which results do you prefer and why?

6. Add one additional lag of both income and consumption to both reduced form equations. Estimate the coefficients of the new reduced forms for both the original and transformed series.
a. Use your results to test for Granger causality for both data series.
b. Which causality results do you find more plausible and why?

7. If the covariance between the structural form error terms is zero, what restrictions does this impose on the reduced form error covariance matrix?

8. Decompose the reduced form error covariance matrix into a lower triangular form using a Cholesky decomposition.

9. Write the two equation reduced form in matrix format and premultiply by the matrix you used in question 8 to turn the covariance matrix into a lower triangular matrix.

10. Use the result from question 9 to comment on the restrictions necessary to produce the result that income does not "cause" consumption.