Practice

The data for this homework consists of monthly data for the period 1981 through 1989, for a total of 108 observations. The data is for California. The dataset is traffic2.wf1. There is also a data description file.

1. During what month and year did California's seatbelt law take effect?
2. Is California's a primary or a secondary seatbelt law? You will have to look this up on the WWW.
3. When did the highway speed limit increase to 65 MPH?
4. Regress the variable log(totacc) on a time trend ('t' in the dataset) and 11 monthly dummies.
   1. Would you say that there is seasonality in total accidents? How do you know?
   2. What is the meaning of the coefficient on the time trend?
5. Add to the regression from part 4. the variables wkend, unem, spdlaw and beltlaw.
   1. Does the coefficient on unem make sense in terms of sign and magnitude?
   2. Are the coefficient estimates for spdlaw and beltlaw what you expected? Why?
6. Repeat part 4., but use log(prcfat), which is pecent of accidents that result in a fatality, instead of log(totacc). Do your conclusions regarding seasonality and time trend change?
7. Go back to the model of with log(totacc) on the left hand side and the time trend, seasonal dummies, wkend, unem, spdlaw and bltlaw on the RHS. Save the residuals by entering the command series res01=resid in the command window, the big white field at the top of the workfile space. Now run the regression res01_t = b₀ + b₁ res01_t-1 + v_t. At the 5% level test the null hypothesis that the coefficient on res01_t-1 is different from zero.
8. For the original model of part 7., in the estimation dialogue box of EVIEWS add the term AR(1) and estimate the model coefficients. Is the estimate of the coefficient on AR(1) the same as the coefficient on res01_t-1 of part 7? If there is a difference, how do you account for the difference?
9. Redo part 7., but also include the set of independent variables on the RHS of res01_t = b₀ + b₁ res01_t-1 . Does your new estimate of b1 differ from your answers in parts 7 and 8?

Theory

Consider the very simple dynamic autoregressive distributed lag (ARDL) model describing the behavior of y in terms of x expressed as follows:

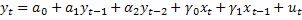                                   (T.1)

Where the error, u_t, is iid N(0,σ²). When the model is in long run equilibrium it must be the case that

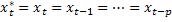
With the consequence that

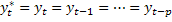
1. What is the short run effect on y of a one unit change in x?
2. What is the long run, equilibrium relationship between y and x?
3. What is the long run effect on y of a one unit change in x?
4.  Is there serial correlation in the error structure of (T.1). If so, write it out.
5. If your answer to the previous question was yes, then derive the error covariance matrix.