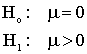
tobs = 1.954/.842 = 2.32
P(-2.32 < t < 2.32)
@ .974 Therefore reject the null.Temple University
Economics 615
Demand for Bread and Meat: Answer Key
1.a.
|
QB = |
1.95423 + |
.029601 Y + e |
|
|
(.842) 2.321 |
(.00852) 3.47 |
1.b.
|
QB = |
.4011 + |
.0245 Y + |
.4129 S - |
.355 PB |
+.57 PM + e |
|
|
(1.03) .39 |
(.00789) 3.10 |
(.112) 3.69 |
(.062) 5.73 |
(.161) 3.54 |
2.
|
|
|
tobs = 1.954/.842 = 2.32 |
|
P(-2.32 < t < 2.32) @ .974 Therefore reject the null. |
3. i.
|
|
|
|
|
|
|
|
|
The observed F is above the critical value for any reasonable significance level, so reject the null. |
3.ii.
|
|
|
tobs = .57/.161 = 3.53 |
|
|
4.
|
i. |
|
|
|
|
|
ii. |
|
|
|
|
|
iii. |
|
|
|
|
|
|
|
|
iv. |
|
|
|
|
|
|
5.
For the meat equation when the observations with Qm=0 are omitted|
QM = |
7.512 + |
.0389 Y - |
.356 S + |
.146 PB - |
1.179 PM + |
e |
|
|
(.95) 7.91 |
(.008) 4.86 |
(.121) 2.94 |
(.061) 2.39 |
(.149) 7.91 |
|
When all the observations are used
| QM = | 7.815 + | .0411 Y - | .4367 S + | .1625 PB - | 1.2293 PM + | e |
| (1.045) 7.47 |
(.008) 5.13 |
(.114) -3.83 |
(.063) 2.56 |
(.163) -7.54 |
a.
| Delete Obs for which Qm=0 | All Observations |
|
|
|
|
|
|
|
|
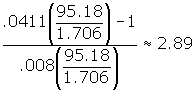
|
|
At the 2.5% level reject Ho |
b.
| Exclude obs for which Qm = 0 | All observations |
|
|
|
|
Define |
.1625+.0411(4.7719)=.3586 |
|
tobs = 6.306 Reject the null. |
.06352+(4.7719)2(.008)2+2(4.7719)(-.0002416)
=.003184 tobs = 6.355 |
6.
Your answers to the meat part of this question will depend on how you dealt with the zeros in QM. The choices are to delete those observations; inadvisable since you lose valuable information. When QM = 0, let ln(QM) = 0; inadvisable since you are saying that these households are equivalent to those that consumed QM = 1. When QM = 0, reset it to QM = (some small number); inadvisable since this will tilt the regression line unduly. Add 1 to every observation on QM; best idea yet, although households with low QM experience a bigger % shift than those with high QM. You should read the text or lecture notes to decide how best to deal with missing data.| Results when observations corresponding to Qm = 0 are deleted from both the Bread and Meat samples: | ||||||
|
LnQB = |
-.5633 (.465) |
+.719 lnY (.162) |
+.33 ln S (.132) |
-1.196 ln PB (.172) |
+.066 ln PM (.16) |
+ e |
|
LnQM = |
-1.833 (1.54) |
+1.514 lnY (.54) |
+.899 ln S (..44) |
+.642 ln PB (.57) |
-2.282 ln PM (.54) |
+ e |
| Use all data for bread and add 1 to Qm. | ||||||
|
LnQB = |
-.6433 (.4207) |
+.7057 lnY (.1319) |
+.37 ln S (.1075) |
-1.1428 ln PB (.1555) |
+.6303 ln PM (.1555) |
+ e |
|
LnQM = |
-.8025 |
+1.213 lnY |
-.847 ln S |
+.5087 ln PB |
-1.782 ln PM |
+ e |
a.
|
|
|
| All observations | Delete obs for which Qm = 0 |
|
|
|
|
tobs = .07581/.09958 = .76126 |
tobs = .761 |
b.
|
|
|
|
|
1.213-.8471-1 = -.6341
|
|
tobs = -1.041 |
tobs = -2.33 |