Hints for "Is Bread Giffin?"
From Henderson and Quandt, Microeconomic Theory, Pp. 27-31, 2nd Edition,
McGraw-Hill, 1971. Another good source is Layard and Walters, Microeconomic Theory, Pp.
123-143, McGraw-Hill, 1978. In what follows pi is the price of the ith
good, qi , and y is income.
- The uncompensated, own-price elasticity of demand is
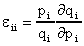 . For the first ratio we usually substitute the sample means for the
respective variables. The second term is the appropriate slope coefficient from the
appropriate regression.
. For the first ratio we usually substitute the sample means for the
respective variables. The second term is the appropriate slope coefficient from the
appropriate regression.
- The uncompensated, cross-price elasticity of demand is
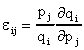 . Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .
. Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .
- The income elasticity of demand is
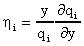 . Yet
again, the first term is approximated by the sample means. The second term is a slope
coefficient.
. Yet
again, the first term is approximated by the sample means. The second term is a slope
coefficient.
- Define the share of income spent on the ith good as
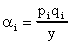 . You can assume that p and y are exogenous. Define the compensated
own-price elasticity as the percentage change in quantity demanded for a small percentage
change in price, while restoring the consumer's real income just enough to leave his
utility unchanged. From the Slutsky equation we can show that the uncompensated, own-price
elasticity of demand is a linear function of the compensated, own-price elasticity and the
income elasticity. That is,
. You can assume that p and y are exogenous. Define the compensated
own-price elasticity as the percentage change in quantity demanded for a small percentage
change in price, while restoring the consumer's real income just enough to leave his
utility unchanged. From the Slutsky equation we can show that the uncompensated, own-price
elasticity of demand is a linear function of the compensated, own-price elasticity and the
income elasticity. That is,
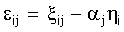 . You know
the uncompensated, own-price elasticity and the income elasticity and can solve for the
unobservable compensated elasticity. Since this is directly derived from the Slutsky
equation, it also holds for i=j.
. You know
the uncompensated, own-price elasticity and the income elasticity and can solve for the
unobservable compensated elasticity. Since this is directly derived from the Slutsky
equation, it also holds for i=j.
- The relationship between the compensated, own- and cross-price elasticities is
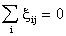 . (Note that there is a typo in H&Q at
(2-19). Compare it to their (2-39). This mistake is in both the 1st and 2nd
editions.) Thus there is another easy way to solve for the compensated cross price
elasticity. What does this 'law' tell you about the compensated elasticities in the two
good case? What does it tell you about substitutes in the many good case?
. (Note that there is a typo in H&Q at
(2-19). Compare it to their (2-39). This mistake is in both the 1st and 2nd
editions.) Thus there is another easy way to solve for the compensated cross price
elasticity. What does this 'law' tell you about the compensated elasticities in the two
good case? What does it tell you about substitutes in the many good case?
- Some other useful facts about elasticities:
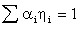 , the share weighted average of the income elasticities is one. And
, the share weighted average of the income elasticities is one. And 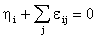 , for the ith good the sum of the
uncompensated own and cross elasticities is equal to the income elasticity.
, for the ith good the sum of the
uncompensated own and cross elasticities is equal to the income elasticity.
- For households in 18th century England (largely agrarian with the bulk of the
population working as subsistence tenant farmers), income and prices were largely out of
their control and are therefore exogenous. In all of the above cases we have linear
combinations of random variables. Constructing test statistics is then quite
straightforward.
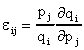 . Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .
. Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .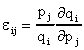 . Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .
. Again, the first term is approximated by the sample means. The
second term is an appropriate slope coefficient .