Temple University
ഀ ഀDepartment of Economics
ഀ ഀIntroductory Econometrics
ഀ ഀHeteroscedasticity Homework
ഀ ഀഀ ഀ
Practice
ഀ ഀFor this problem set use the datasetഀ
on home characteristics and prices. The
1. Local government and public schools are largely financed by propertyഀ taxes. One's property tax bill is based on the tax rate and the assessed valueഀ of the house. From time to time the local tax authority must revise theഀ assessed values of houses in the jurisdiction. To bring some regularity to theഀ re-assessment process the authority often uses regression models. The datasetഀ hprice1.wf1 has data on assessed value and house attributes. It is your job toഀ help with the modeling of home attributes and assessed value.
ഀ ഀa. Estimate by OLS the regression coefficients of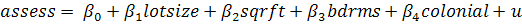 
and report your results.
b. For the same model as that in part a, use EVIEWS to find theഀ heteroscedasticity robust standard errors for the coefficients and report yourഀ findings.
ഀ ഀc.Compare and contrast your results for parts a and b.
ഀ ഀd. Use EVIEWS to conduct a Breusch-Pagan test for heteroscedasticity at theഀ 5% level and report your results.
ഀ ഀe. Revise the model to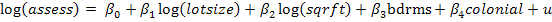 
by taking logs of assess, lotsize and sqrft,ഀ
but not bdrms. Conduct a Breusch-Pagan test for heteroscedasticity atഀ
the 5% level.
f. In reviewing your resutls for aprts d and e, did transforming the dataഀ mitigate the heteroscedasticity problem in any way?
ഀ ഀTheory
ഀ ഀ2. Consider the linear regression model
and every subsequent group ofഀ
three rows is identical to this first group. The error covariance matrix Ω isഀ
diagonal, with typical diagonal element equal to 
, where ω > 0 and x2tഀ
is the tth element of the second column of X.
a. What is the variance of 
, the OLS estimator of 
?
b. What is the probability limit, as n →∞, of the ratio of the conventionalഀ
estimate of this variance, which assumes homoscedasticity, to aഀ
heteroscedasticity consistent estimate based on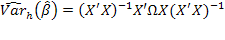 
?