A Brief Introduction to Vector Autoregressions
Introduction
The basic premise is that we can use the interaction among several variables to improve our forecast of each individual variable. At time t the forecast of a variable y is a function of its own past values as well as the present and past values of other variables in the system. The basic premise is that structural systems models of the economy have done a poor job of forecasting. As an alternative, some modelers have proposed using atheoretic vector autoregressive (VAR) models. A VAR does not come with the set of exclusion restrictions necessary to identify and estimate a structural model. As a consequence, both Keynesians and Monetarists could use the same VAR to forecast GDP.
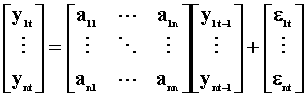
As in univariate analysis of the last chapter, the simplest model is a first order process, VAR(1). Since this is the easiest specification to deal with, we'll use it almost exclusively. Most of the results stated here can be generalized to higher order VAR processes. We'll write the first order process as
![]()
![]()
The matrix A is an nxn matrix of unknown coefficients. The error terms have expectation zero, are independent over time, but may be contemporaneously correlated, so the nxn error covariance matrix need not be diagonal. A little thought probably suggests to you that the AR system is just a reduced form for some unstated structural model.
If yt is a stationary random vector then an equivalent moving average representation can be derived. The process yt is stationary if and only if the roots of the determinantal equation
![]()
where L is an n-dimensional lag operator, lie outside the unit circle. The infinite order MA representation is
![]()
where B = (I-AL).
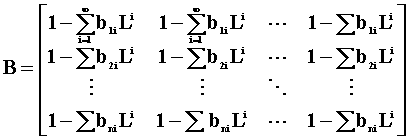
Conversely, if yt is a finite MA and the roots of |B|=0 are outside the unit circle, then the process is invertible and can be rewritten as a possibly infinite order autoregression.
To pursue the different representations a bit further, the process might be a mixed AR(p) and MA(q). Hence
![]() .
.
If the AR part is stationary then the model can be rewritten as a MA, possibly of infinite order. Similarly if the MA part is invertible then the process can be written as an AR, possibly of infinite order.
To avoid the problem of determining p and q in the vector ARMA, we often write the model as a VAR of arbitrary finite order. Since the right hand side variables will all be past realizations of y:(nx1), it is possible to apply OLS to estimate the unknown coefficients in the matrix A.
Alternative Representations
To proceed we'll consider the two variable VAR(1) given by
![]()
![]()
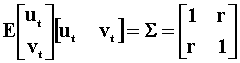
According to the model, an increase in ut will cause xt to increase by one unit and will cause yt to increase by r units as well. Because of the contemporaneous covariance between u and v, a change in v cannot be attributed to a pure innovation in y.
The moving average representation of the system can be derived by recursive substitution and written as
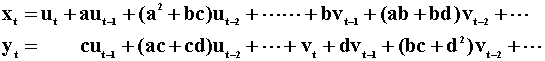
Notice that the MA representation of x does not include the current value of v, nor does the MA representation of y include the current value of u. Is this contrary to the earlier assertion that a one unit innovation in xt will cause yt to increase by r units? No, since the contemporaneous correlation between u and v is r. A one unit change in u produces an r unit change in v, which does enter the MA rpresentation of y. To pursue this, we proceed by first writing the model in matrix form:
|
|
.. 1 |
The innovations in this system of equations are given by
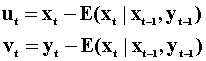
The information set for xt is xt-1 and yt-1. Similarly for yt it is xt-1 and yt-1.
The Cholesky Decompostion,
the lower triangular square root such that ![]() , of the error covariance
matrix is
, of the error covariance
matrix is
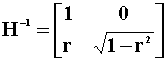
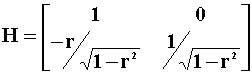
Multiply both sides of the VAR by H to get the recursive model
|
|
.. 2 |
The new error terms are given by
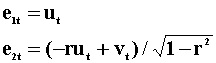
and they have zero correlation. The innovations in this second model are given by
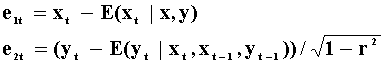
The information set for x and y is now different than that for the first representation.
In model ..2 there are no endogenous variables in xt, but the current value of xt appears in yt. Hence an innovation in x in the first equation has a direct effect on y. In representation 2 a change in ut has no effect on yt by construction.
The moving average representation of the system has the same sort of
characteristic. Derive the MA model from ..2
|
|
.. 3 |
The current value of e2 does not appear in xt, but the current value of e1 does appear in yt. We have a second triangularization of the same system. Now a change in e1t by one unit produces a change of r units in y, although e1 and e2 are still uncorrelated.
Finally, these three triangularizations are not unique. Their representations depend on the ordering of the variables in the model. If we were to put y first, then we would get a different set of relationships. The only circumstance under which ordering doesn't matter is when u and v are uncorrelated.
Exogeneity
With all of these representations, an obvious question is whether x or y or vice are exogenous. In this usage we interpret the word 'expgenous' in the sense of a variable being determined outside the system. There are several different notions of exogeneity. In order to understand them all we'll first have to consider the general vector ARMA model, then look at our specific two variable case.
|
|
.. 4 |
The nx1 dimensional random vector y has been partitioned into y1:n1x1 and y2:n2x1. The error vector has been partitioned conformably. y1 is strictly exogenous with respect to y2 when it is not affected either directly or indirectly by lagged values of y2. If c12(L)=0, then lagged values of y2 do not affect y1. If d12(L)=0 and d21(L)=0 then lagged values of y2 do not enter the y1 equation. These three restriction matrices are necessary and sufficient. Let's impose the restrictions and multiply through by the inverse of the MA coefficient matrix to get the VAR representation:
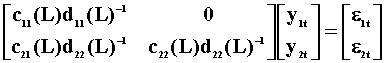
This gives us the necessary and sufficient condition for the exogeneity of y1 with respect to y2. In the VAR representation, y1 is exogenous with respect to y2 if and only if the coefficients on y2 are all zero.
Now impose the exogeneity restrictions and multiply the ARMA in ..4 by the inverse of the AR coefficient matrix to get the MA representation of the system.
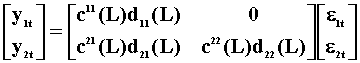
Hence, in the MA representation of the system, y1 is exogenous
with respect to y2 if and only if the coefficients on ![]() are all zero.
are all zero.
Sometimes you will see reference to the notion of weak exogeneity.
The idea is similar to that of sufficient statistics. A statistic is sufficient
if the likelihood function can be factored into a part that depends on the
statistic and the unknown parameter and a part that depends only on the data.
The weak exogeneity of y1 with respect y2 requires
knowledge of the joint likelihood function for y1 and y2,
say ![]() . If this can be factored into the product of two likelihood
functions
. If this can be factored into the product of two likelihood
functions ![]() such that
such that ![]() can take any values in its
parameter space given a specific admissable value for
can take any values in its
parameter space given a specific admissable value for ![]() .
.
There is also the notion of a variable being predetermined. The variable y2
is said to be predetermined if it is unaffected by present and future values of
![]() but is affected by
past values of
but is affected by
past values of ![]() .
.
To cement these notions we again consider a simple model
|
|
.. 5 .. 6 |
The disturbances ut and vt are independent and serially uncorrelated. Since xt is correlated with the error term in eqn 5, and similarly for yt in eqn 6, we need to solve for the reduced forms.
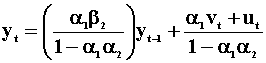
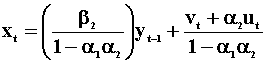
Note that these reduced forms are actually two AR(1)'s
that are related through their error terms and are a special case of the
alternative representations that we considered earlier. If ![]() then the reduced form for xt becomes
then the reduced form for xt becomes ![]() . xt is now no longer contemporaneously
correlated with the error ut, although it
will be affected by past values of u through yt-1. We say that xt is predetermined.
. xt is now no longer contemporaneously
correlated with the error ut, although it
will be affected by past values of u through yt-1. We say that xt is predetermined.
Suppose that ![]() and
and ![]() so that xt = vt.
Now xt is independent of past, present and
future values of ut, and it is said to be
strictly exogenous.
so that xt = vt.
Now xt is independent of past, present and
future values of ut, and it is said to be
strictly exogenous.
Suppose that all we really needed was a consistent and asymptotically
efficient of ![]() in
equation 5. If
in
equation 5. If ![]() in equation 6 then xt and ut are contemporaneously uncorrelated so an OLS
estimate of
in equation 6 then xt and ut are contemporaneously uncorrelated so an OLS
estimate of ![]() will be
consistent and asymptotically efficient. In this case xt is said to be weakly exogenous for
will be
consistent and asymptotically efficient. In this case xt is said to be weakly exogenous for ![]() . If u and v had a joint
normal distribution you could prove this using the factorization suggested
above.
. If u and v had a joint
normal distribution you could prove this using the factorization suggested
above.
Suppose we now wish to use our estimate of ![]() and equation 5 to forecast yt+1 for
a given xt+1 .
If
and equation 5 to forecast yt+1 for
a given xt+1 .
If ![]() , then yt tells us what xt+1
must be and the forecasted yt+1 tells us what xt+2 via
equation 6. As a result of this feedback we are not able to pick any value we
wish for xt+2 . We cannot use equation 5 in
isolation from equation 6 for forecasting purposes. If
, then yt tells us what xt+1
must be and the forecasted yt+1 tells us what xt+2 via
equation 6. As a result of this feedback we are not able to pick any value we
wish for xt+2 . We cannot use equation 5 in
isolation from equation 6 for forecasting purposes. If ![]() , then we are able to use
equation 5 in isolation for forecasting. In this instance xt
is said to be strongly exogenous in equation 5.
, then we are able to use
equation 5 in isolation for forecasting. In this instance xt
is said to be strongly exogenous in equation 5.
Finally, suppose xt in equation 5 is a
policy variable. If ![]() is
invariant to policy changes then xt is
said to be super-exogenous.
is
invariant to policy changes then xt is
said to be super-exogenous.
Causality
To examine the notion of Wiener - Granger causality in a two variable system we introduce two summary tables. The first lays out the notation and models, the second presents the results. Each pair of rows is a model. Hence there are four models.
|
Table
1 The Models |
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
|
||
|
Var(ujt)=Tj |
Var(wjt)=Gj |
Cov(u2t, w2t)=C |
|
|
||
The third model, the 5th and 6th rows are found by
pre-multiplying the second model, the 3rd and 4th rows, by 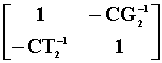 .
.
|
Table
2 Wiener Granger Causality |
||
|
(1) z causes x if and only if |
||
|
|
or |
G1 > G2
|
|
(2) x causes z if and only if |
||
|
|
or |
T1 > T2 |
|
(3) z does not cause x if and only if |
||
|
|
or |
G1 = G2 |
|
(4) x does not cause z if and only if |
||
|
|
or |
T1 = T2 |
|
(5) There is instantaneous causality between x and z if and only if |
||
|
|
or |
T2 > T3 |
Exogeneity and causality are not the same thing. Tests for the absence of a causal ordering can be used to refute strict exogeneity in a given specification, but such tests cannot be used to eatablish it. Furthermore, unidirectional causality is neither necessary nor sufficient for inference to proceed on a subset of variables, all we require is that the variables be weakly exogenous.
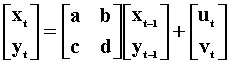
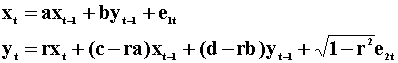
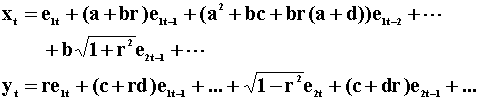
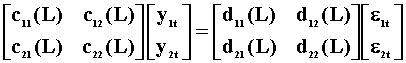
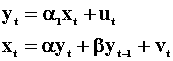
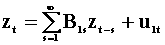
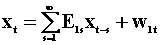
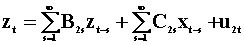
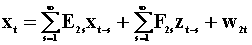
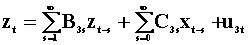
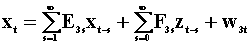
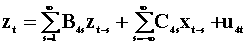
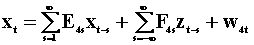
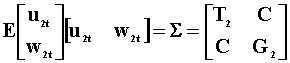
 for all s
for all s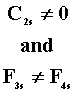 for all s
for all s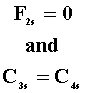 for all s
for all s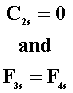 for all s
for all s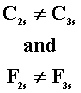 for all s
for all s