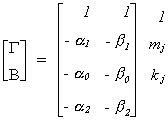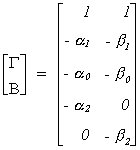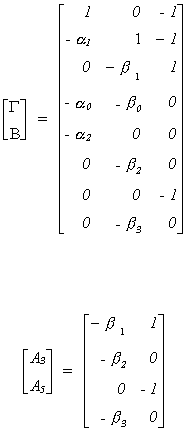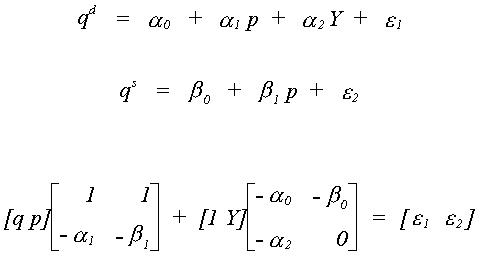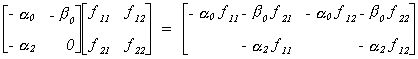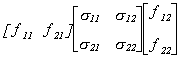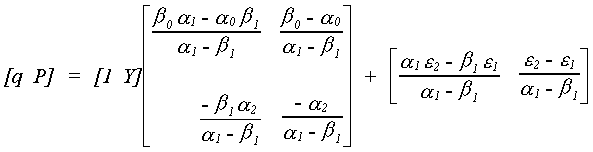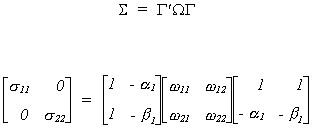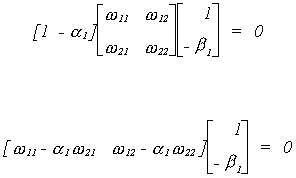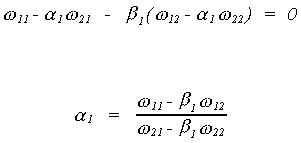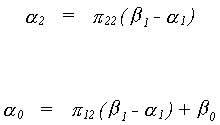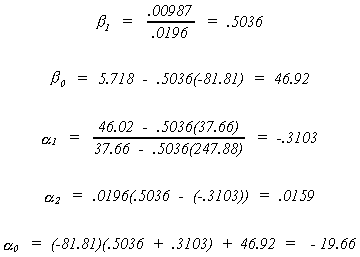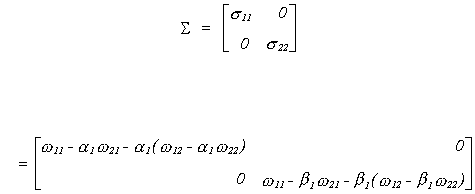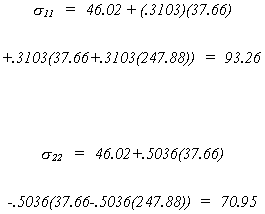6. Simultaneous Equations
6.1 The Problem
6.1.1 Graphical Views of the Identification Problem
A Three Dimensional View of Supply and Demand
A Two Dimensional View of How the Data are Generated
In both graphical views you should have noticed that fitting a line by OLS to the observed
data will incorrectly estimate the unknown slope coefficient. If you didn't catch this, go
back and look again.
6.1.2 A Specific Example
Consider the simple macroeconomic model
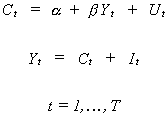 (6.1)
(6.1)
C is consumption, Y is real GDP and I is investment and is assumed to be non-stochastic.
Substituting and solving for the two behavioral variables
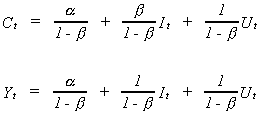 (6.2)
(6.2)
In our model (6.1) is known as the structural system and (6.2) is known as the reduced
form.
The first problem that we encounter in systems models is best addressed by
rewriting the reduced form and doing a bit of tedious algebra.
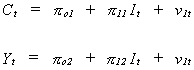 (6.3)
(6.3)
Applying OLS to these equations we can estimate the set of ps
consistently since the RHS variable is independent of the error term. Referring back to
(6.2) we see that we can construct an estimate of b from two
different equations. For this example the numerical results will be identical. Can you
prove it?
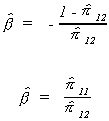
In this example in which the two numerical results are the same we are lucky, the first
equation is said to be identified.
The second problem that we encounter in systems models has to do with properties of
estimators. It is illustrated by continuing the example. Suppose that we apply OLS to
(6.1) to obtain an estimate for b
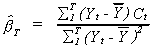
Both Yt and Ct are random variables so it is hard to evaluate 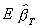 . We can, however, evaluate the probability
limit.
. We can, however, evaluate the probability
limit.
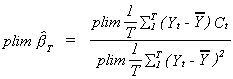
Consider first the denominator
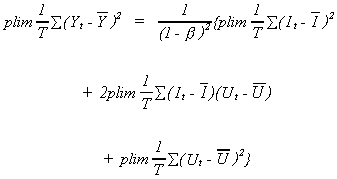
which was derived by substituting from (6.2). So
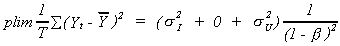
Turning now to the numerator
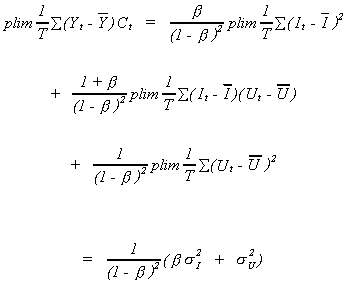
Putting the pieces back together
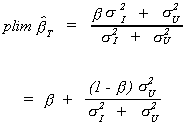
In the context of the model we are considering, we know that the MPC, b, is between zero and 1. We can see from the above result that even
in large samples we over-estimate b.
A simple graphical representation shows the effect of the consistency problem on the magnitude of over-estimation.
To summarize the results of this section, we have seen that we can always estimate the
parameters of the reduced form consistently. This is not necessarily the case for the
structural form. If it is possible to consistently estimate the parameters of the reduced
form, under what circumstances can we construct point estimates of the structural
parameters form the reduced form results? When is there enough information in the reduced
form to just identify the structural parameters? If the application of least squares to
the reduced form provides too much information, are there alternative estimation
techniques which enable us to use the excess?
In what follows we explore the two problems of systems models in greater detail. In the
next section we explore the identification problem. After that we take up different
methods of estimation. In the final section we consider some special testing procedures
for systems models.
- Identification
The classic paper in this area is E.J. Working, "What Do Statistical Demand Curves
Show?" Quarterly Journal Of Economics, Vol. 41, No. 1, February 1927. The most
definitive treatment is Franklin Fisher, The Identification Problem in Econometrics,
Robert E. Krieger Publishing Co., Huntington, N.Y., 1976.
In this section we begin by introducing some notation. Then the problem of
identification is introduced by exploring three simple cases. From there we go to a more
general treatment with retrospective looks at the three special cases.
Suppose we have the structural model
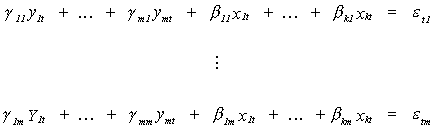
The first subscript identifies the variable, the second subscript identifies the
equation. Thus, we have the same number of endogenous variables as we have equations, m.
There are k exogenous variables. Converting to matrix form we can write
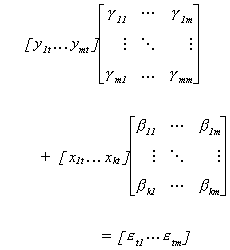
Be sure to note that the columns of the coefficient matrices correspond to the
structural equations. Also, an observation on all the variables is arranged as a row. In
order to avoid having to write so much, we write the structural model as
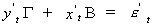
We proceed as follows to get the reduced form
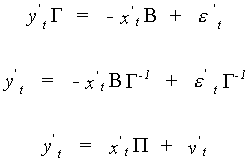
Can you state the order of all the matrices in this representation? In terms of all the
observations the structural model can be written
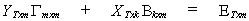
The subscripts indicate the dimensions of the matrices.
We turn now to a specification of the error variance. For the structural model we have
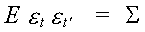
S is an mxm matrix of contemporaneous covariances between the
equation error terms.
For the reduced form we have
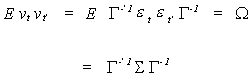
Identification by Exclusion Restrictions
EXAMPLE 1 An Underidentified System
We have a demand equation and a supply equation, respectively:
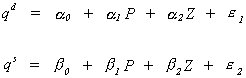
in which the exogenous variables are denoted by Z, and the endogenous variables are P and
q. Writing things in matrix form
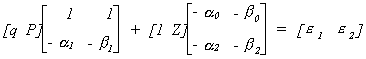
The reduced form is found as follows
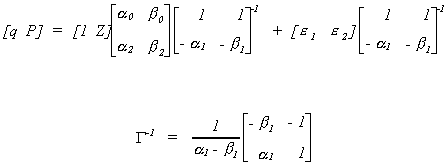
After doing all the algebra we come up with
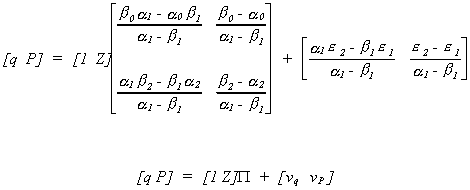
Note:
1. We have four equations in six unknowns from the reduced form equations.
2. Alternatively
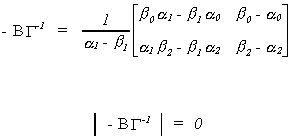
The rank of the matrix of the reduced form coefficients is not 2, it is only 1.
3. Also, in each equation of the structural model we have 2 included endogenous variables
and no excluded exogenous variables.
The issue of rank and counts of included endogenous and excluded exogenous variables will
prove crucial in our discussion of the identification problem.
EXAMPLE 2 An Exactly Identified System
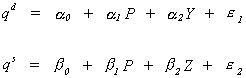
Writing things in matrix form
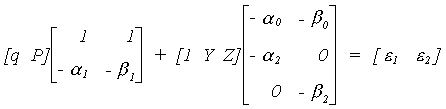
The reduced form is as follows
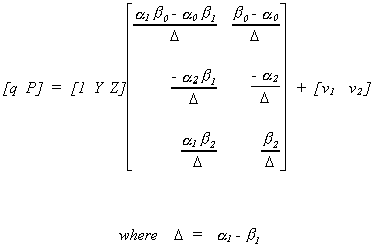
Note:
1. Now we have 6 equations and 6 unknowns from the reduced form.
2. The rank of  is 2 and the number of
endogenous variables is 2.
is 2 and the number of
endogenous variables is 2.
3. In each structural equation we have an excluded exogenous and 2 included endogenous
variables.
EXAMPLE 3 An Overidentified Macroeconomic Model
The model has three equations. Two of them are behavioral: consumption, c, and
investment, i. The third is the national income,y, identity that expenditures must equal
income in equilibrium. The exogenous variables include the interest rate, r, government
spending, g, lagged consumption, c-1, and lagged income, y-1. The
structural model is
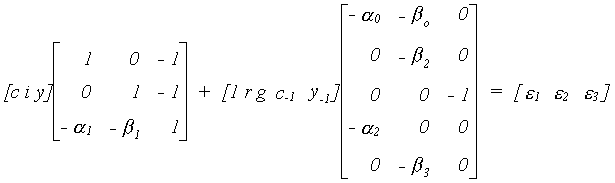
Since the last equation is an identity, e3 is a
degenerate random variable. That is, its variance is zero.
The reduced form, which you could derive with a pencil and paper or using a program like
Mathematica or MathCAD, is as follows
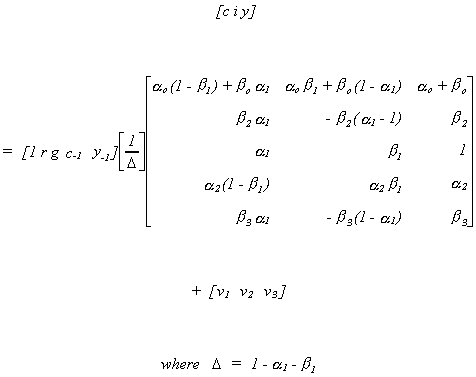
Note:
1. There are 15 equations in 7 unknowns in the reduced form.
2. The rank of P is three and there are three endogenous
variables.
3. There are two included endogenous variables in each equation of interest. The first
equation has 3 excluded exogenous, the second has equation has 2 excluded exogenous, and
the third equation has 4 excluded exogenous variables.
THEOREM: The Order Condition
k*j ³ mj
The number of excluded exogenous variables must be greater than the number of endogenous
variables found on the right hand side of equation j.
This theorem is a straightforward matter of counting. It is a necessary but not sufficient
condition for an equation to be identified.
Before we can introduce The Rank Condition we need some new notation for the
reduced form equations. Everyone knows you can't tell the players without a scorecard. The
following table provides some vital statistics for the elements of the reduced form shown
below the table.
Player
|
Description
|
Dimension
|
| yj |
dependent variable in the jth structural equation
|
1 x 1
|
Yj'
|
endogenous variables on the "RHS" of the jth
structural equation
|
1 x mj
|
Y*j'
|
endogenous variables NOT appearing in the jth structural
equation
|
1 x m*j |
xj'
|
included exogenous variables of the jth structural equation
|
1 x kj
|
Xj*
|
excluded exogenous variables of the jth structural equation
|
1 x kj*
|
pj
|
reduced form coefficients on the exogenous variables included in the jth
structural equation
|
kj x 1
|
pj*
|
reduced form coefficients on the exogenous variables excluded from the jth
structural equation
|
kj* x 1
|
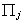
|
coefficients of exogenous variables, # of rows corresponds to the number
of included exogenous variables in the jth equation, # of columns corresponds
to the number of included endogenous variables in the jth equat ion
|
kj x mj
|
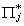
|
coefficients of exogenous variables, # of rows corresponds to the excluded
exogenous variables of the jth equation, # of columns corresponds to included
endogenous variables
|
kj* x mj
|
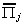
|
coefficients of exogenous variables, # of rows correspond to included
exogenous variables, columns correspond to excluded endogenous variables
|
kj x mj*
|
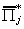
|
coefficients of exogenous variables, rows correspond to excluded exogenous
and columns correspond to excluded endogenous variables
|
kj* x mj*
|
vj
|
reduced form error corresponding to the LHS variable of the jth
structural equation
|
1 x 1
|
Vj'
|
reduced form error vector corresponding to the RHS endogenous variables of
the jth structural equation
|
1 x mj
|
Vj*
|
reduced form error vector corresponding to the endogenous variables
excluded from the jth structural equation
|
1 x mj*
|
The left hand side of the system of reduced form equations has been partitioned
according to whether and where an endogenous variable is included in the structural form.
The right hand side has then been partitioned conformably.
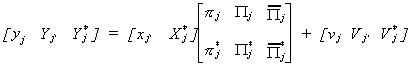
Recall that 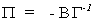 so we can write the matrix of
endogenous structural coefficients as
so we can write the matrix of
endogenous structural coefficients as 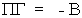 .
The jth column of B corresponds to the jth structural equation. To get these we need just the
jth column of G.
.
The jth column of B corresponds to the jth structural equation. To get these we need just the
jth column of G.
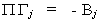
Now Gj
is the set of coefficients for the endogenous variables of the jth structural equation, or
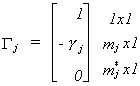
Combining this with our representation of the partitioned reduced form we get
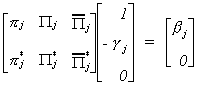
Carrying out the multiplication allows us to write this as two equations 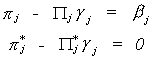 The second equation gives us a system of kj*
non-homogeneous equations in mj unknowns. The order condition follows from this
obviously. From linear algebra we know that there is a unique solution,
The second equation gives us a system of kj*
non-homogeneous equations in mj unknowns. The order condition follows from this
obviously. From linear algebra we know that there is a unique solution, 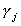 to the system of non-homogeneous equations if
and only if Rank(
to the system of non-homogeneous equations if
and only if Rank(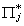 ) = mj.
) = mj.
THEOREM: The Rank Condition
The jth equation is identified IFF Rank(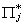 )
= mj. That is, the rank of
the kj* x mj matrix of reduced form coefficients
corresponding to include endogenous - excluded exogenous variables must be mj.
)
= mj. That is, the rank of
the kj* x mj matrix of reduced form coefficients
corresponding to include endogenous - excluded exogenous variables must be mj.
Example 4 (Example 1 again)
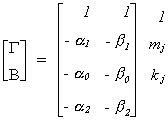
We can interpret the above using Greene's terminology. The coefficients of
the jth equation have been moved to the first column. The coefficients of the
remaining equations are in the last m-1 columns. The rows have been rearranged according
to the dependent variable, the included endogenous variables, excluded endogenous
variables, included exogenous variables, and excluded exogenous variables. The first row
of the remaining columns corresponds to Green's A1, the next row corresponds to A2 (included endogenous variables), there is
no A3 (excluded endogenous),
the final kj=2 rows
correspond to A4 (included
exogenous), there is no A5
(excluded exogenous).
Since mj* = 0 and kj* = 0 neither equation is
identified.
Example 5 (Example 2 again)
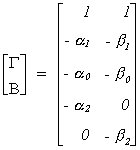
The coefficients of the jth
equation have been moved to the first column. The coefficients of the remaining equations
are in the last m-1 columns. The rows have been rearranged according to the dependent
variable, the included endogenous variables, excluded endogenous variables, included
exogenous variables, and excluded exogenous variables. The first row of the remaining
columns corresponds to Green's A1,
the next row corresponds to A2
(included endogenous variables), there is no A3
(excluded endogenous), the next 2 rows correspond to A4 (included exogenous), the last row is A5 (excluded exogenous).
Note mj* = 0 and kj* = 1. A5 has rank 1, equal to the number of included endogenous
variables so the equation is identified.
Example 6 (Example 3 again)
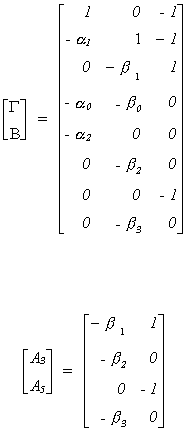
The matrix of coefficients has been rearranged using Greene's scheme. First, the
coefficients of the equation of interest are moved to the first column. Then the rows are
rearranged. The first row is the row of the dependent variable, A1. The second row carries the included coefficient of
the included endogenous variable, A2.
The third row is the excluded endogenous variable, A3. The fourth and fifth rows are for the included
exogenous variables, A4. The
final three rows correspond to the excluded exogenous variables, A5.
The augmented matrix (A3, A5) has rank 2 and there is one included
endogenous variable. The first equation is over identified.
Identification by Covariance
Restrictions
We return to the underidentified supply and demand model.
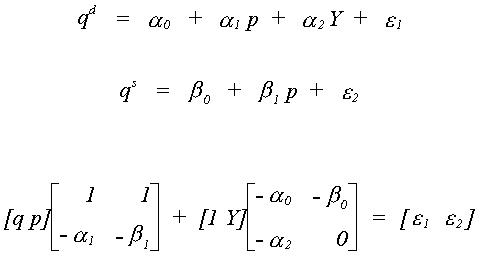
We want to see if it is possible for there to be a false structure. That is, can we
find a set of restrictions that provides us with two equivalent structures. Or, BF = B*, where B*
must have the same pattern of zero and nonzero terms as B.
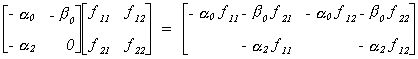
So we conclude that f12 =
0.
The covariance for the false structure is
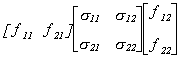
Suppose we know that s12 = s21 = 0. Then
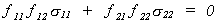
Since f12 = 0 it must be that
either f21 = 0 or f22 = 0. If the latter is true then there would be no
second equation so we conclude that f21
= 0 and the only admissible value for f11
and f22 is one.
Recall that the reduced form for the model is
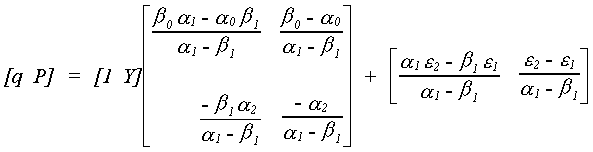
For the supply equation
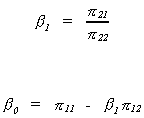
We know the relationship between structural and reduced form covariances to be
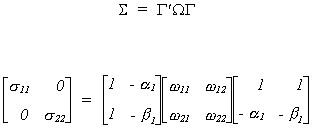
Since we are interested in only off diagonals we need not do all of the multiplication
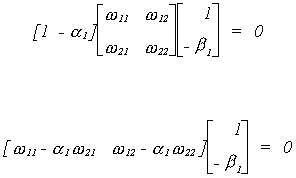
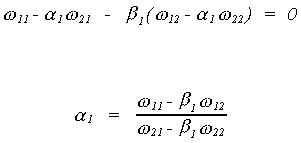
And then
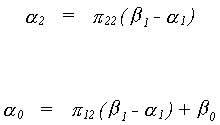
Using the data in Greene we can complete the example as
follows
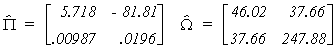
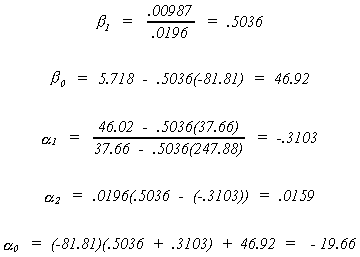
For the structural error covariance matrix
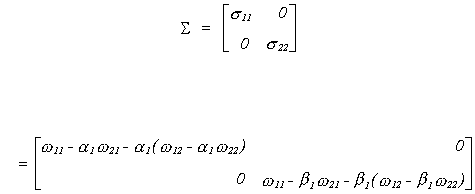
Using the data in Greene we can calculate the equation variances as shown below.
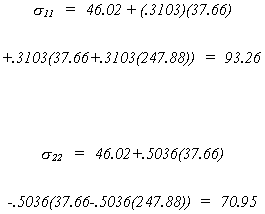
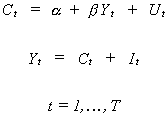 (6.1)
(6.1)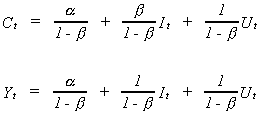 (6.2)
(6.2)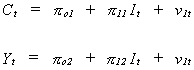 (6.3)
(6.3)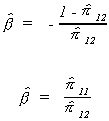
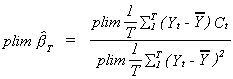
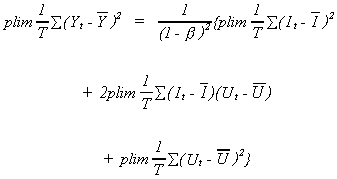
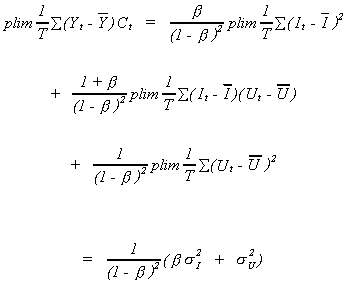
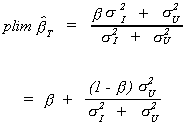
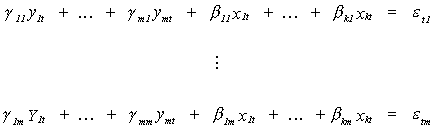
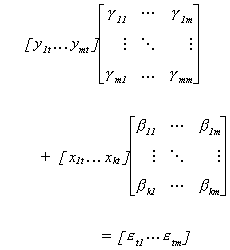
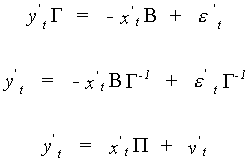
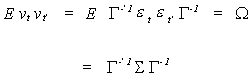
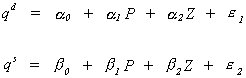
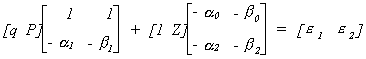
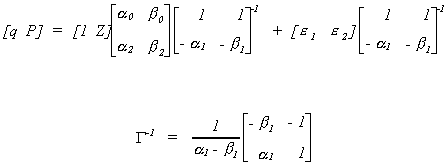
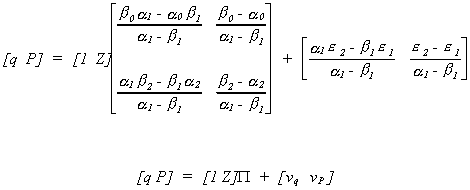
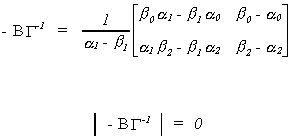
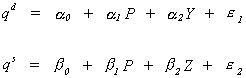
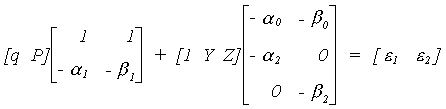

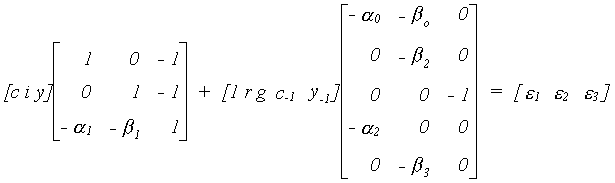
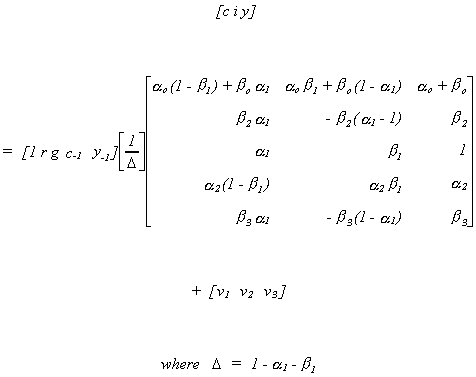
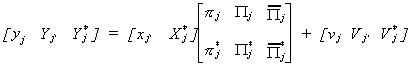
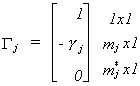
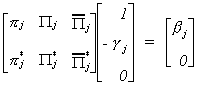
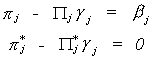 The second equation gives us a system of kj*
non-homogeneous equations in mj unknowns. The order condition follows from this
obviously. From linear algebra we know that there is a unique solution,
The second equation gives us a system of kj*
non-homogeneous equations in mj unknowns. The order condition follows from this
obviously. From linear algebra we know that there is a unique solution,