Notes on Likelihood Ratio, Wald and Lagrange Multiplier Tests

Consider the random variable Y~N(). The unrestricted parameter space for Y is . However, on the basis of, say, an economic model, we have some belief about . We can represent this belief in the form of a null hypothesis and its alternate:

We have no conjecture about the possible value of . The null hypothesis defines a subspace of which we will term the restricted parameter space, denoted by . Within and are particular values of which maximize the likelihood function. We can evaluate the likelihood function at the sample data based choices for which maximize the likelihood function. Denote those points as . The empirical likelihoods will have the same sign and, based on the principle of maximum likelihood, . Hence, . If the ratio is close to one then it must be the case that the restricted and unrestricted values of which maximize the likelihood must be approximately the same. If the ratio is close to zero then the restricted and unrestricted values of must be quite different. The problem then is to choose a critical value, , so that , where is the chosen significance level of the test. One would reject the null hypothesis for small observed values of . For our example, in which Y has a normal distribution and is known, the likelihood ratio turns out to be (Can you derive this?), which we compare with . Taking logs of both sides and rearranging a bit we get




and

and

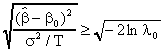
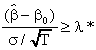
This is recognizable as the test statistic based on the standard normal random variable. If were unknown, then the distribution of the test statistic would be Student's t.

Suppose that we have a random variable Y with known variance, , and unknown mean,. It may be that we do not know the distribution of Y, but that its first two moments are finite. In large samples, then, we do know that the distribution of the sample mean is . We rely on this fact in what follows.

Let L() be the log likelihood function, a single unknown parameter in the unrestricted parameter space , and is the maximum likelihood estimator of . As before, the hypothesis we want to test is

The restricted parameter space, , consists of the single point . One constructs the likelihood ratio . Under the null hypothesis where J is the number of restrictions on the parameter space. In this case J=1. The following figure depicts the test statistic.


If the values of and are far apart, then L() and L() will be far apart, the test statistic will be large, and we will reject the null hypothesis.

The Wald Statistic

You can see from the above picture that the size of the test statistic will depend on both - and the curvature. If L() is getting steeper at a faster rate, then LR/2 will be larger. Now consider another figure, shown below. Although the difference - is the same for the two likelihood functions, L^a and L^b based on two datasets, the value of the test statistic will differ. It will be larger for the test based on the dataset used for L^b by virtue of the fact that the likelihood function is getting steeper at a faster rate. The curvature of the likelihood is measured by the negative of its second derivative evaluated at the unrestricted estimator, . The larger this derivative, the steeper the slope of the likelihood function.


The curvature is given by

The fact that the test statistic will be affected by the curvature of the likelihood suggests that we rescale - by the second derivative of the likelihood function. Doing so gives the Wald statistic:


Under the null hypothesis the Wald Statistic is distributed as . One rejects the null for large values of W.

Return to the notion of maximizing the likelihood function. But now consider the possibility that we might want to impose what we believe to be true under the null hypothesis at the time we solve the maximization problem. That is, we could solve the constrained maximization problem

Differentiating with respect to and setting the results equal to zero yields the restricted maximum likelihood estimator, , and the value of the lagrange multiplier, , where S(.) is the slope of the likelihood function, , evaluated at the restricted estimator. The notation S(.) is delibrate as the test statistic is also referred to as the score test. The greater the agreement between the data and the null hypothesis, i.e. , the closer the slope will be to zero. Hence, the lagrange multiplier can be used to measure the distance between and .
There is a small problem. Consider two data sets, a and b, from which L^a and L^b are calculated and plotted in the following diagram:



You can see that for data set 'a', the distance will be greater than that for data set 'b'. The two data sets would also produce different likelihood ratios (you should be able to pencil this argument in the diagram). However, both likelihoods have the same slope at ! This is an undesirable result. Again, the curvature of the likelihood function is seen to be the culprit; at the function L^a has a smaller second derivative than does L^b. This suggests the lagrange multiplier statistic

This is distributed as and we reject the null for large observed values of the test statistic.