The correct model is y* = bx* + e but we do not observe or measure the data correctly. Possibly what we observe is
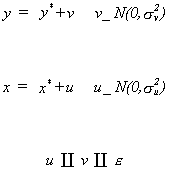 1
1 DATA PROBLEMS: Measurement Error
The correct model is y* = bx* + e but we do not observe or measure the data correctly. Possibly what
we observe is
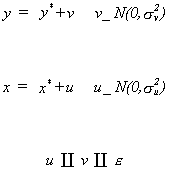
We will consider a few cases, begining with the easiest. Suppose that we can observe x*,
but not y*. Then our model will be, on substitution into (1),
This is nothing more than our usual regression problem since e
and v are independent of each other and x*. The fact that the error term is the
sum of two independent random variables does not require any special treatment.
We go on from here by looking at the case where x* is measured with error.
Observe that x = x* + u so the regressor is correlated with the
disturbance.
Which clearly violates the classical assumption of independence between the right hand
side variables and the error term. We can assess the impact on the OLS estimator as
follows
Multiply the numerator and denominator by 1/n and expand the products under the sums
The second termn is the ratio of two random variables, albeit normal, so expectations
are not straightforward. Intuition/common sense tells us that the expectation is not zero.
We can use the Slutsky Theorem to evaluate the probability limit of the OLS estimator.
In the numerator the first three terms are zero. The last is -bsu2.
In the denominator the first term is . The
fourth term is
. Putting the pieces
together we get
The conclusion is that OLS is not consistent, and converges on a point below the true
value for b. The moral is that even in large samples we cannot
estimate b consistently since there are four unknowns b, se2, su2, and Q*, but we have only three
pieces of information. The total sum of squares for the dependent variable, Syy,
converges to b2Q* + se2,
the total sum of squares for x, Sxx, converges to Q* + su2, and the cross product between the
dependent and independent variable, Sxy, converges to bQ*.
There are a few proposed solutions to the dilemma.
Method 1
Assume a different distribution for e and u so that we can
use the higher order moments constructively.
Method 2
If the data for the model is time series then we can exploit a feature of
economic data. Namely, we can use the fact that it is often highly serially correlated.
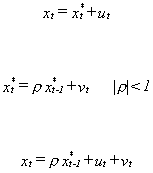
substitute in recursively
Now substitute back into the original model
Applying OLS to the recast model
Numerator and denominator cancel so the OLS estimatro is both unbiased and consistent.
There does not seem to be as easy a solution when the data is cross section.