Before going into details, a simple example (or choose the *.mcd file) will help you visualize what is going on.
For an R-script with output and a LIMDEP output that both deal with random effects models skip down ot the bottom of this page.
3.2 Set Up
There are i=1,...,N individuals observed over t=1,...,T periods and we posit the
relationship
(1)
When we have the same number of observations for each person the experimental design is
known as a balanced block design. When the blocks are unequal all of the follwoing results
hold, but only after some corrections.
Depending on the circumstance, we might also represent the model in one of two alternate
forms
or
where e is an NTx1 vector of ones, a is the corresponding
intercept, Z are the remaining k-1 columns of X and d are slope
coefficients.
Note the following:
1) We presume that all individuals have the same response to changes in the independent
variables. The coefficients to be estimated are equal across persons and periods. That is,
they all have the same MPC in a consumption model.
2) We might think that there are random effects across individuals. That is, at all points
in time, a change in an unobserved variable affects each individual differently, but the
effect is fixed over all the periods. Also, there may be a random effect in each period
that affects all individuals in the same way. Finally, there may be unobservables that are
random through time and across individuals.
Thus, we can decompose our error term as follows
mi represents the individual effects
lt represents the time effect
nit represents the purely random or white noise
effect
We make the following assumptions about the components of the error
That is, each component of the error term has a mean of zero.
The variance of the individual effect is the same for all persons, although the
realization of the disturbance may differ across persons. Further, there is no correlation
between persons.
The variance of the time effect is the same for all periods, but the realization differs
from period to period. There is no serial correlation. If the time subscript does not
match then the expectation is zero.
The expectation of the white noise product is non zero only when both the individual and
time subscripts match.
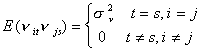
Let us construct the covariance matrix for the population disturbance. We'll do this
one piece at a time, starting with the individual effect
Given our assumption about the individual random effect, we can write the covariance
matrix for the ith person's random effect as
eT is a column vector of ones of dimension Tx1. When we stack all of the
individuals one over the other, the pattern of individual effects variances is
This is a great big matrix of dimension NTxNT. There are a total of N blocks on the
main diagonal, each of which is TxT. Each block is filled with the common variance. Every
other position is filled with a zero.
Similarly for the time effect, we first stack the observations, running first through the
time subscript then incrementing the individual subscript
Consider first the time effect covariance between person i and person j
This is a scalar diagonal matrix because the time subscripts match between the ith and
jth persons.
For any given person we have
Putting everyone back together
This NTxNT matrix is composed of TxT scalar diagonal matrices everywhere.
Consider now the white noise term.
Anywhere that both the individual and time subscripts match we get a nonzero
expectation.
The result is a big, NTxNT, scalar diagonal matrix.
Putting together the three pieces we get the patterned matrix
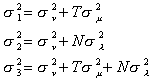
The strategy that we employ is to go through the data the first time to obtain sets of
residuals which are then used to construct estimates of the parameters in the error
covariance matrix. As a strategy, this is similar to what you did to correct for
autocorrelation using the Cochrane Orcutt technique.
Step 1.a
Construct a cross section regression by finding the mean of T observations for each
individual. That is,
Notice several things: We have shifted the position of the disturbance mi and that Slt = 0.
One way to interpret this formulation would be to assert that the intercept is random.
Parenthetically, P.A.V.B. Swamy extended this notion to make all of the regression
coeffcients random.
The estimator applied to this equation is known as the between estimator and is equivalent
to applying least squares to
Q1 is a matrix which puts the data in a form that provides one data point
per person; we have only N observations now. Q1 is idempotent and has a trace
of N-1. Each person's time mean is measured as a deviation from the grand mean. The result
is that we lose the intercept. Hence, Xs refers to the set of independent
variables excluding the column of ones for the intercept. An equivalent OLS formulation
would be to use the original data, but include a dummy variable for each distinct person
(no intercept then). Suppose that you have a cross section of time series on wages, the
dependent variable, and schooling, the independent variable. Ability is an omitted
variable that serves to shift the intercept across individuals. The question is whether
the shift is random or fixed? You specify a random effects model. The result is that there
will be a correlation between schooling and the error term. The testing procedure for
discriminating between the least squares dummy variable model and the random effects model
exploits this fact.
Let us look at the residual sum of squares for the 'between' estimator.
Taking the trace and expected value we have
Let us consider the term involving sl2.
We are particularly interested in the product of Q1 and the Kronecker product
term.
with some manipulation we can show that this is zero so the sl2
term drops out.
Now consider the sm2 term, the relevant
portion of which we reproduce here
Let us look specifically at the part involving the product of Q1 and the
Kronecker product.
The trace of this we can see to be NT - T, or T(N-1).
We also want to take advantage of the following property
If you multiply through by T/T you can see that we get TQ1Q1.
Since Q1 is idempotent this is just TQ1. Therefore, when we put
together some of the pieces involving the sm2
we can write
Therefore
So, using the residuals from the 'between' estimator,
is an unbiased estimator of . In the above equation the .
indicates that we have already summed out the time effects
Step 1.b
Construct a time series regression by finding the mean of N observations at each point
in time. That is,
Applying least squares to this equation is the 'within' estimator encountered in the
analysis of variance. This estimation equation could be written as
where Q2 is given by
Each observation is measured as a deviation of the mean across individuals for the tth
period from the grand mean. The OLS equivalent to the 'within' estimator would be one
which included a dummy variable for each time period (no intercept in that case).
Notice that we have shifted the position of the disturbance lt
so that it is closely associated with the intercept. Again there is the question of
whether the appropriate model is fixed effects or random effects. If we incorrectly
specify the RE, then the error term will be correlated with the RHS variables. Also, Smi = 0. Note that the intercept can again be thought of
as a random term with non-zero mean. From this regression we can save the residual sum of
squares to construct
which we can show to be unbiased using the same methods as applied in step 1.a. The .
indicates that we have summed out the individual effects.
Step 1.c
We will now use time, state, and overall means to construct
There is no intercept in this model. It is equivalent to applying least squares to a
model that has all the variables measured in their levels, but which has a set of dummies
for individuals and a set of dummies for time periods. It is sometimes referred to as the
least squares dummy variables model or, in ANOVA, the fully saturated model. The algebraic
form taken by the saturated model is
Save the residuals from this model and construct
which is also unbiased.
Step 2.a
Form the coefficients
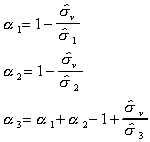
where .
Step 2.b
Construct the transformed variables
Step 2.c
Now you are ready to estimate the parameters of
3.4 Properties of the Estimator
We will consider two step estimators in general, of which
is a particular example.
THEOREM
Consider the model
we can regard this as a set of N equations with each equation having T observations.
Assume that the disturbances in the different equations U1(t), ..., UN(t)
follow a t-dimensional continuous probability law, symmetric about zero. That is, f(U1(t),
..., UN(t)) is an even function.
Then
where is an unbiased estimator of W-1,
is itself unbiased. Also assume U has a fourth moment and E(1-r-w)-1 exists.
Proof:
In part a. of the proof we show that the expectation of the estimator exists and in
part b. we show that the estimator is unbiased.
a. Let h denote any vector of real numbers from NT dimensional
space and consider the expectation of
Recall Y = X b + U, so we will make this substitution also
Recall the Cauchy Schwartz Inequality
For our problem we will adopt the following definitions
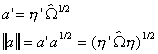
and
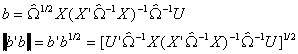
Substituting into
Recall from our unit on linear algebra that if A-B is positive semi definite then
Z'(A-B)Z ³ 0. For our problem we'll let
So upon taking the difference
Factoring the square root of out of this expression gives us
The part in square brackets is idempotent so must be positive semi-definite. The square
root of the inverse of the error covariance estimator, , is also
positive semi definite. Therefore A - B is positive semi definite and we can conclude that
and that
Therefore
Now introduce the following definitions
so that for the model as stated at the start of the theorem we can write
The largest and smallest characteristic roots of the estimated error covariance matrix
are
From two theorems of linear algebra
Substituting these results into
Finally
Since all three terms on the right are finite we can conclude that
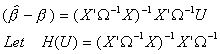
Note that is an even function of U, and therefore H(U) is also
even. Now
is an odd function and is isomorphic about zero. So
H(U) and f(U) are even, U is odd, so the integrand is odd. Therefore, E()=0.
3.5 Testing the Specification
A. Random Effects vs. OLS
Our test statistic will be
where . That is, the set of residuals is saved from applying
OLS to the whole sample. In this case our test statistic is distributed as
.
We note the following
The first of these sums the OLS residuals over time for each individual and squares the
n results, then adds them up. The sum can be thought of as an estimate of the numerator of
s12=su2+Tsm2. The second sums the OLS residuals over
individuals for each period and squares the T results, then adds them up. The sum can be
thought of as an estimate of the numerator of s22=su2+Tsl2.
Under the null hypothesis sm2 and sl2 are both zero, so the terms in square
brackets in the test statistic are zero.
B. Fixed Effects vs. OLS
The test statistic is
C. Random Effects vs Least Squares Dummy Variable Model
1. The REM assumes that, for example, individual effects are uncorrelated with the
other regressors. In the example provided earlier wages were regressed on schooling and we
acknowledged that ability was an unobservable that could serve to shift the intercept.
Now, if we had data on the entire population then LSDV would surely be the appropriate
model. But since we are drawing only a sample REM might be appropriate. That is, the
intercept varies in a random fashion across individuals due to sampling. The problem is
that the random effect attributable to ability might be correlated with schooling.
2. If the random effects are correlated with other regressors then the random effects
estimator is inconsistent due to omitted variables. Recall we raised this possibility of
specification error earlier in the discussion.
Ho: No correlation. LSDV and REM are both consistent, LSDV is not efficient.
Therefore the REM is the better estimator.
H1: Correlation. REM is not consistent, so use LSDV.
Under Ho LSDV and REM will not differ systematically, so we look at
We know
A result due to Hausman is the following
Using this
Note that the variances in S exclude any terms corresponding
to dummy variables and intercepts. It is based solely on the slope coefficients.
A Wald statistic is then
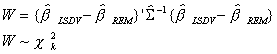
An example is provided in another section of the lecture notes.
_______________________________________________________________________
Random Effects, R and LIMDEP
_______________________________________________________________________
The R-script is
## Example of Random Effects model from Venables and Ripley, page 205
library("nlme")
library("regress")
data(Oats)
names(Oats) <- c("B","V","N","Y")
Oats$N <- as.factor(Oats$N)
## Using regress
oats.reg <- regress(Y~N+V,~B+I(B:V),identity=TRUE,print.level=1,data=Oats)
summary(oats.reg)
## Using lme
oats.lme <- lme(Y~N+V,random=~1|B/V,data=Oats,method="REML")
summary(oats.lme)
The corresponding output for the REGRESS command is
Maximised Residual Log Likelihood is -214.975
Linear Coefficients:
Estimate Std. Error
(Intercept) 79.917
8.220
N0.2
19.500 4.250
N0.4
34.833 4.250
N0.6
44.000 4.250
VMarvellous 5.292 7.079
VVictory -6.875
7.079
Variance Coefficients:
Estimate Std. Error
B
214.477 168.834
I(B:V) 109.693 67.711
I 162.559
32.191
The corresponding output for the LME command is
Linear mixed-effects model fit by REML
Data: Oats
AIC BIC
logLik
586.0688 605.7756 -284.0344
Random effects:
Formula: ~1 | B
(Intercept)
StdDev: 14.64549
# 14.64549^2 = 214.477
Formula: ~1 | V %in% B
(Intercept) Residual
StdDev: 10.47060 12.75034
# 10.4706^2 = 109.693 and 12.75034^2 = 162.559
Fixed effects: Y ~ N + V
Value Std.Error DF t-value
p-value
(Intercept) 79.91667 8.219989 51
9.722235 0.0000
N0.2
19.50000 4.250113 51 4.588114
0.0000
N0.4
34.83333 4.250113 51 8.195861
0.0000
N0.6
44.00000 4.250113 51 10.352667 0.0000
VMarvellous 5.29167 7.077578 10
0.747666 0.4719
VVictory -6.87500 7.077578
10 -0.971378 0.3543
Correlation:
(Intr) N0.2 N0.4 N0.6
VMrvll
N0.2
-0.259
N0.4
-0.259 0.500
N0.6
-0.259 0.500 0.500
VMarvellous -0.431 0.000 0.000
0.000
VVictory -0.431
0.000 0.000 0.000 0.500
Standardized Within-Group Residuals:
Min
Q1
Med Q3
Max
-1.84137227 -0.66274193 -0.06682795 0.63830229 1.66054158
Number of Observations: 72
Number of Groups:
B V %in% B
6 18
Output from LIMDEP
Fixed Effects
+----------------------------------------------------+
| Ordinary least squares regression |
| Model was estimated Jan 19, 2006 at 10:04:23AM |
| LHS=YIELD Mean = 103.9722 |
| Standard deviation = 27.05913 |
| WTS=none Number of observs. = 72 |
| Model size Parameters = 6 |
| Degrees of freedom = 66 |
| Residuals Sum of squares = 30179.08 |
| Standard error of e = 21.38361 |
| Fit R-squared = .4194761 |
| Adjusted R-squared = .3754970 |
| Model test F[ 5, 66] (prob) = 9.54 (.0000) |
| Diagnostic Log likelihood = -319.5402 |
| Restricted(b=0) = -339.1178 |
| Chi-sq [ 5] (prob) = 39.16 (.0000) |
| Info criter. LogAmemiya Prd. Crt. = 6.205292 |
| Akaike Info. Criter. = 6.204905 |
| Autocorrel Durbin-Watson Stat. = .8174727 |
| Rho = cor[e,e(-1)] = .5912637 |
+----------------------------------------------------+
+---------+--------------+----------------+--------+---------+----------+
|Variable | Coefficient | Standard Error |t-ratio |P[|T|>t] | Mean of X|
+---------+--------------+----------------+--------+---------+----------+
Constant 79.9166667 6.17291691 12.946 .0000
N2 19.5000000 7.12787048 2.736 .0080 .25000000
N3 34.8333333 7.12787048 4.887 .0000 .25000000
N4 44.0000000 7.12787048 6.173 .0000 .25000000
V1 -6.87500000 6.17291691 -1.114 .2694 .33333333
V3 5.29166667 6.17291691 .857 .3944 .33333333
+--------------------------------------------------+
| Random Effects Model: v(i,t) = e(i,t) + u(i) |
| Estimates: Var[e] = .255399D+03 |
| Var[u] = .214681D+03 |
| Corr[v(i,t),v(i,s)] = .456689 |
| Lagrange Multiplier Test vs. Model (3) = 80.50 |
| ( 1 df, prob value = .000000) |
| (High values of LM favor FEM/REM over CR model.) |
| Baltagi-Li form of LM Statistic = 80.50 |
+--------------------------------------------------+
+---------+--------------+----------------+--------+---------+----------+
|Variable | Coefficient | Standard Error |b/St.Er.|P[|Z|>z] | Mean of X|
+---------+--------------+----------------+--------+---------+----------+
N2 19.5000000 5.32707415 3.661 .0003 .25000000
N3 34.8333333 5.32707415 6.539 .0000 .25000000
N4 44.0000000 5.32707415 8.260 .0000 .25000000
Constant 79.3888889 7.06887251 11.231 .0000
Notice that Greene's Var(u) is quite close to the Variance due to the Block effect in R|REGRESS. For this data set LIMDEP's estimator was not able to find positive estimates of the variances when there were random BLOCK and Variety effects.