1.8 Review of Hypothesis Testing
1.8.1 Some Basics
We have the general linear model
1
where Y is nx1, X is nxk, b is kx1 and U is nx1. The
population disturbance is distributed according to
So the Aitken estimator is
which can be rewritten in terms of the population disturbance as
(2)
The sampling distribution of our estimator, for suitable assumptions about the
distribution of U or the sample size, is
We would estimate the scalar in the covariance matrix from either the least squares
approach or the maximum likelihood approach
Proceeding with the least squares estimator of the error variance, the quadratic form
in the numerator can be written as
or
8 (3)
which is distributed as
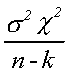
with n-k degrees of freedom. Note that the matrix A has rank n-k.
Returning to (2), we can rearrange the expression for the estimator as
which is distributed as
You should be able to show with a bit of algebra that BA=0. This is, of course, the
necessary and sufficient condition for a 2 and a normal to be independent. We
also know that
where L is kx1 and l is a scalar. Our test statistic is
where the estimate of the error variance is constructed from the residuals of the
unrestricted regression.
The numerator is a linear combination of normal random variables and is therefore normally
distributed. You may recall from equation (2) of the previous section that the estimator
is a linear combination of random variables in the regression error vector. The same
section shows that the denominator is a chi-square. Hence the ratio is a t-statistic.
1.8.3 The Garden Variety F-test
Suppose we have the null and alternate
where R is jxk and r is jx1. The rank of R must be j<k. That is, the joint set of
restrictions must be linearly independent and there must be fewer of them than the number
of unknown coefficients.
We construct an estimate of b for the unrestricted parameter
space. I.e.,
And we use this to construct an estimate of the restriction, i.e.,
Under the null we have
We have been assuming normality so under null, in both small and large samples,
Therefore
is distributed as 2 with j degrees of freedom.
We already know
to be 2 with n-k degrees of freedom so the ratio of the two will be F(j,n-k)
with a noncentrality parameter of zero under the null hypothesis. We read the appropriate
critical value from a central F table. Under the alternate hypothesis the test statistic
is distributed non-centrally. This is a result of the fact that the numerator is
constructed from squared normal random variables which do not have a zero mean. When the
null is false, therefore, we get a draw from a distribution that is more highly skewed
than the F under the null. That is, we are more likely to observe more extreme
F-statistics. This is a small sample test.
It is also worth noting that the conventional F-test is very conservative. That is, the
restrictions are believed to hold absolutely under the null. If they are incorrect by even
a little bit then we want to reject the null. At the same time, we know that the variance
of the restricted least squares estimator is smaller than that for the unrestricted OLS
estimator. This suggests that the preferred estimator might not be that which has minimum
variance among unbiased estimators and we might not want to base our test statistic on
that estimator.
By definition we have MSE = Variance + Bias2. Under the null hypothesis as
usually stated, the restrictions are identically correct, we recognize that the MSE of the
OLS estimator is the same as its variance
For our restricted least squares estimator we had
Combining these we get the MSE for the RLS estimator
We want to choose the estimator with the smaller MSE. Taking the difference between
the two gives us
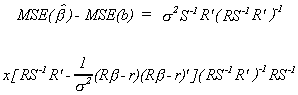
So our null hypothesis is that the two MSE are the same and the alternate is that MSE
for the RLS is greater than that for OLS.
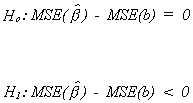
Recalling (*), we see that it is the difference between two quadratic forms which can
be factored as
We are interested in whether this is > 0. Think of it as a quadratic form of the
sort B'AB, which we saw to be positive definite if, for B nonsingular, A was positive
definite. So we are curious about the middle term
for all l not identically zero. Or
Or,
From the Cauchy-Schwartz inequality we know that this ratio can never be greater than
31 (ii)
and reaches a maximum if we choose
If A is positive definite then we know Q £ 1 for any l,
including lo. Since lo gives the maximum of Q and is
known to be less than 1, we can write
Remember, in constructing the F-test we assumed that . If it does not then the F-statistic is noncentral with
noncentrality parameter
This noncentrality parameter can be as big as ½, on the basis of the argument above,
before the difference between the MSEs goes negative. Thus we read our critical values
from an F table with a noncentrality parameter equal to ½.
Our criterion for choice of estimator might be to compare
These two terms are the average squared distance from our estimator to the true
parameter value for OLS and RLS, respectively. They happen to be equal to the traces of
the MSEs. So now we are interested in
we can show that this trace is positive only if
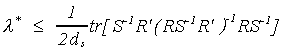
where ds is the smallest
characteristic root of the matrix of which we are taking the trace. Our null is specified
as (iii) being true. We construct the usual F statistic, but read our critical values from
noncentral F tables with noncentrality parameters equal to the observed .
1.8.6 Large Sample Tests
These lecture notes are only a primer. A very good survey article is Robert F. Engle,
Chapter 13: Wald, Likelihood Ratio, and Lagrange Multiplier Tests in Econometrics,
in Handbook of Econometrics, Vol. II, edited by Z. Griliches and M.D. Intriligator,
Elsevier Publishers BV, 1984.
1.8.6.1 A Large Sample Estimator
Again we specify
where Y is nx1, X is nxk, b is kx1 and U is nx1. The
population disturbance is distributed according to
The log likelihood for the sample is
We can do a change of variable and do some rearranging to get
Taking derivatives with respect to the unknown parameters gives us the well known
first order conditions
Solving the first order conditions gives
Our parameter estimates then have the distribution
which is distributed as
under the null hypothesis.
So Wald suggests the test statistic
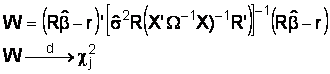
The estimate of the error variance is constructed using the residuals from the
unrestricted model, i.e., the alternate hypothesis with all of the variables included. The
reason is that you do no harm if you use the unrestricted model, even when the
restrictions are true. Elsewhere we show that if you include irrelevant variables the
least squares estimator remains BLU. However, if you omit relevant variables then your OLS
estimator is biased. Then the linear combination of least squares estimates is not normal
with mean zero, so the Wald statistic is not a central chi-square.
Through suitable manipulation we can write the Wald statistic as
where e is the residual vector when we account for the restrictions under the null,
U hat is
the set of residuals when the parameter space is not restricted, and the estimate of
sigma 2
is constructed from the residuals when the restrictions are not imposed.
1.8.6.3 The Likelihood Ratio Test
The likelihood function when there are no restrictions on the parameter space we
know to be
In order to incorporate the restrictions in the likelihood function we could construct
where is a jx1 random vector. That is, there are j restrictions on the coefficient
vector. Take partial derivatives with respect to the unknown parameters and set these
first order conditions equal to zero. Solving the first order conditions we get
so we are able to construct two estimates of the likelihood function
from the unrestricted model and
from the restricted model. The likelihood ratio statistic is
With suitable manipulation we get
Note that the estimate of the error variance is now based on both the residuals from
the model with the restrictions under the null imposed and on the unrestricted model
residuals. e and have the previous
definitions.
1.8.6.4 The Lagrange Multiplier Test
Returning to the Lagrangian of the previous section we have
The first order conditions from the maximization problem are
The interpretation of l is that it is the gain in
likelihood from easing the constraints. That is,
Anyway, if we solve for l we get
which is distributed as
Therefore
The estimate of the error variance is based on the restricted model. Or, equivalently,
is found from the first order conditions.
Suitable manipulation would give us
where e and have the previous
definitions.
1.8.6.5 Relation Between the Tests
In the above example, if we were to know both W and s2, the three tests are numerically identical.
In the example as constructed, we had to estimate s2.
The results show that although the three test statistics are c2
with j degrees of freedom, they will differ numerically in practice.
When both W and s2 are
estimated then the differences between the observed values of the test statistics will
differ more markedly.
There are potentially two sets of estimates of W. We can
construct an estimate of W in the restricted parameter space,
denote it . Or, it can be estimated in the
unrestricted parameter space, denote it as
.
Then, in terms of residuals, the Wald statistic becomes
where eR is the set of residuals when we use in the construction of
and
is the set of
residuals when we use
in the construction
of the unrestricted estimator, . The Lagrange multiplier statistic is
where eu is the set of residuals when we use in the construction of
and
is the set of residuals
when we use
in the construction of the
unrestricted estimator,
. Finally, the
likelihood ratio statistic is
Now it can be shown that
but since they are all asymptotically c2 with
the same degrees of freedom the critical point is always the same. Invariably this can
lead to some conflict in whether one decides to reject the null.
There is also a graphical relationship
The Lagrange multiplier is based on the slope of the likelihood function at the restricted
estimator. The Likelihood ratio test is based on the difference of the likelihood function
evaluated at the restricted and unrestricted estimates; i.e., the range of the likelihood.
The Wald test is based on the difference between the restricted and unrestricted
estimators; i.e. the domain of the likelihood function.
1.8.7 Decision Rules for Specification
Introduction
A truly classical statistician would be appalled by the use to which economists put
Student's t and F tests. In the classical world the researcher formulates a hypothesis,
collects data, estimates the model parameters, and tests the hypothesis. The presumption
is that the hypothesis to be tested is a true reflection of the world. Regardless of the
outcome of the test, the classical researcher does not use the test of hypothesis to
respecify the model and reestimate from the same data.
In practice economists use the classical testing procedure as a decision rule for model
selection: Choose that model which has the highest F; omit those variables which do not
have significant t-statistics. The level of significance of the test, the probability of a
Type I error is almost always somewhat arbitrarily chosen by the researcher. By choice of
test and sample size the researcher is also choosing the probability of a Type II test. It
is the choice of these two probabilities that determines the loss that the researcher is
willing to incur in making an incorrect decision.
The situation may be pictured as in figure x.x. In the a
(probability of a Type I error), b (probability of a Type II
error) plane the convex line S represents the attainable error probabilities. The family
of concave curves is a set of indifference curves showing the trade-off that the
researcher is willing to make between the two types of errors. Utility increases as one
moves closer to the origin. The optimal choice should be at E. If this should correspond
to the usual 1%, 5% or 10% level of test chosen by researchers it would surely be
coincidence.
If a model is to be chosen in a mechanistic fashion then the loss function should be
clearly stated at the outset. One way to do this is to choose the model which is most
informative about the data. An information criterion permits the researcher to choose a
model under the double consideration of accuracy of estimation and best approximation to
reality.
The Akaike Information Criterion (AIC)
Begin by defining g(Y) as the density function of the true probability distribution
G(Y) for a vector random variable Y' = (y1, y2, ..., yn). Let f(Y|q)
be a model for the unknown g(Y) where q e
Q is a vector of parameters. Then a Kullback-Liebler
Information Criterion (KLIC) for measuring the adequacy of the model is
The KLIC is a measure of the information received from an indirect message. That is,
observing the proposed model tells us something about the unknown model. It is a decrasing
function. Therefore, when the proposed model is close to the truth we are not surprised by
the outcome and I(G(Y):F(Y|q)).
The obvious shortcoming is that the measure depends on the unknown g(Y). If the true
density were known then it would be possible to establish a decision rule for choosing
among alternative models. Suppose one is entertaining two possible models, f1(Y|q) and f2(Y|x). If I(G(Y): F1(Y|q)) < I(G(Y):F2(Y|x)) then
the preferred model is f1(Y|q).
Because the KLIC depends on an unknown distribution function one must construct an
estimator. Assume that I(G(Y): F(Y|q)) is twice continuously
differentiable with respect to q. Define a pseudo true
parameter as one that satifies the inequality I(G(Y): F(Y|qo))
< I(G(Y):F(Y|x)) for any qeQ.
Satisfying this inequality is necessary and sufficient for qo
to be pseudo true. The pseudo true parameters may be found from the evaluation of
.
Assuming that G(Y) = F(Y|q) almost everywhere, Akaike has
shown that
is an almost unbiased estimator of the KLIC. k is the number of parameters in q. Given two alternative models one bases the decision on the model
with the smallest Akaike Information Criterion.
Implied Critical Value of the AIC
Suppose that we are considering a general model, W,
and its nested alternative, w, with k1 and k2
unknown coefficients, respectively. Our job is to choose the better of the two on the
basis of the empirical results from a sample of size n. We can write the difference
between the AICs for the two models as
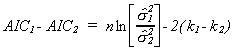
When the difference is less than zero we choose W and when
it is greater than zero we choose w. Making one's decision on
this basis is equivalent to checking the inequality
Or, raising both sides to the n power and subtracting 1 from both sides
If the random variable on the left is less than the right hand side then one chooses
model W. Since the random variable W is based on sums of
squared residuals it is known to have an F distribution, multiplied by a constant. In
particular
Therefore the implied critical value in using the minimum AIC decision rule is
One can compute this for any given problem and look up the probability in the
appropriate table. For example, suppose k1=5, k2 = 3 and n=30. The
implied critical value is 1.78 for an F with 2 and 25 degrees of freedom. This is an
implied level of test of about 20%. This is a much higher level of test than would have
been chosen by anyone applying the conventional F-test in a model selection application.
Since the implied critical value is an increasing function of n it is obvious that with an
increasing sample size the level of the test will decline.