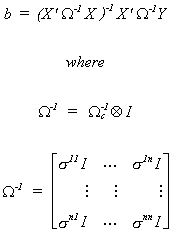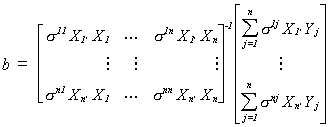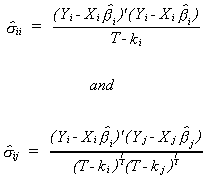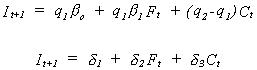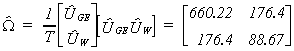4. Seemingly Unrelated Regression
4.1 The Problem
There may be several equations which appear to be unrelated. However, they may be
related by the fact that
1. some coefficients are the same
2. the disturbances are correlated across equations
3. a subset of right hand side variables are the same, although all observations are not
the same.
The estimator proposed here was developed by Zellner. The classic example uses Grunfeld's
investment data. This estimator was the basis for the development of three stage least
squares.
4.2 Set Up
We suppose that the ith equation in a set of n
equations is given by
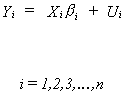
where Yi is Tx1, Xi is Txk, bi is kx1, and Ui
is Tx1. The whole set of n equations can be written as 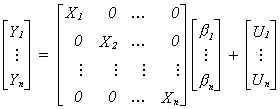
or more compactly as 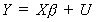 The error
variance-covariance matrix is
The error
variance-covariance matrix is
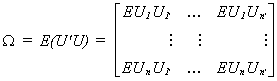 (4.1)
(4.1)
Each diagonal term is a TxT variance-covariance matrix for the disturbance of the ith equation. The off-diagonal TxT blocks are contemporaneous and
lagged covariances between errors of pairs of equations. We assume the following
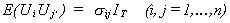 (4.2)
(4.2)
For any given equation the disturbance is homoscedastic and non-autocorrelated. For
i¹j we have non-zero correlation between contemporaneous terms
of the two equations, but zero correlation between lagged disturbances. Substituting 4.2
into 4.1 we have 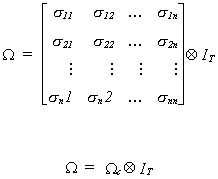 Note that W is of full rank.
Note that W is of full rank.
Caveats
- If the between equation covariances are zero then there is no advantage to applying
Zellner's SUR. It is equivalent to OLS. However, larger covariances mean that there is a
larger efficiency gain in using SUR.
- If the same data is used in each equation, the actual numbers are the same, then there
is no advantage to applying Zellner's SUR. It is equivalent to OLS. The more dissimilar
the Xs, the greater the gain in using SUR.
Estimation
When W is known we can construct the BLUE estimator
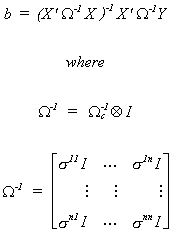
The BLU estimator may be written as
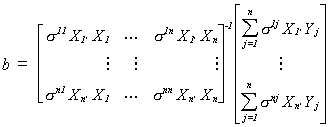
As a practical matter we often don't know W and must
estimate it. A proposed two step procedure is as follows: 1.a. Fit the n equations
separately to obtain the residual vectors
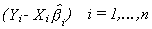
1.b. Estimate the variances and covariances as
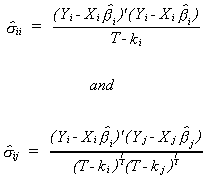
1.c. Use the 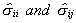 to obtain S-1 as an estimate of W-1.
to obtain S-1 as an estimate of W-1.
2. Construct 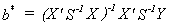 The proof from the
random effects - error components chapter can be adapted to show when b*
is unbiased.
The proof from the
random effects - error components chapter can be adapted to show when b*
is unbiased.
NOTES
- One could use a likelihood ratio statistic to test for non-zero covariances between
equations. The test statistic is
-
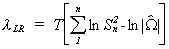
where Sn2 is the
estimate of the error variance when applying least squares to each equation individually
and W is the estimate of the error covariance matrix when there
are contemporaneous cross equation covariances. The number of degrees of freedom for this c2 is n(n-1)/2.
2. Occasionally you will see the Zellner estimator iterated. That is, estimate the
slopes by OLS, construct an estimate of the error covariance matrix, reestimate the
slopes, reestimate the error covariance matrix, and so on. The iterated estimator can be
shown to be the maximum likelihood estimator. However, the estimator outlined above is the
feasible generalized least squares estimator. Therefore there is no gain from applying the
iterations. In large samples the ML and FGLS estimators have the same properties.
An Example
Investment = f1(expected profits)
expected P = f2(value of
outstanding stock at end of year)
Ft = market value at end of year
Ct* = desired
capital stock where Ct*
= bo + b1 Ft
Ct = existing capital stock
By substitution we see that desired net investment is Ct* - Ct = bo + b1 Ft - Ct
Let the fraction of desired net investment that is actually realized be denoted by q1. Then realized net investment is 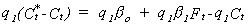
Depreciation investment is q2Ct
so
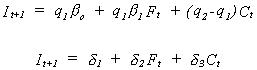
We have data on Westinghouse and G.E. for the period 1935-1954. Estimating the
parameters for the two companies separately
G.E.: It = -10.0 + .027 Ft-1
+ .152 Ct-1 Rbar2 = .671
(.016) (.026)
West: It = -.5 + .053 Ft-1
+ .092 Ct-1 Rbar2 = .714
(.016) (.056)
The numbers in parentheses are standard deviations of the coefficients. The estimated
error covariances are 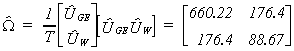
Our test statistic for non-zero covariances, with one degree of freedom is
lLR = 20 (
ln(660.22)+ln(88.67) - ln(660.22 x 88.67 - 176.42))
lLR = 15.16
This is a good deal larger than the critical value for any reasonable level of
significance so we reject the null hypothesis of diagonal covariance matrix. If we use the
fact that the contemporaneous covariances are not zero then the results change slightly to
G.E.: It = -27.7 + .038 Ft-1
+ .139 Ct-1
(27.00) (.013) (.023)
West: It = -1.3 + .058 Ft-1
+ .064 Ct-1
(7.0) (.013) (.049)
The standard errors of the coefficient estimators have narrowed some. It is also
possible to see the efficiency gain in two dimensions.
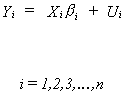
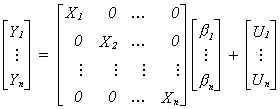
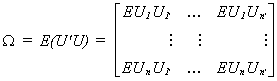 (4.1)
(4.1) 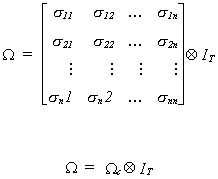 Note that W is of full rank.
Note that W is of full rank.