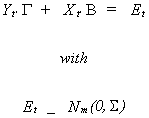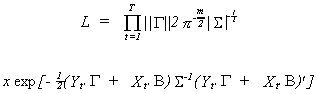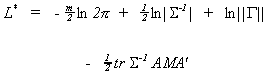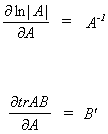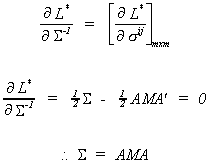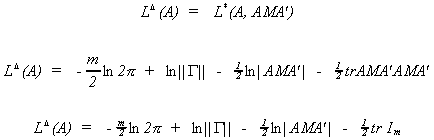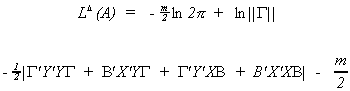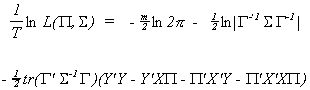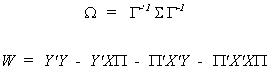6.3 Estimation
6.3.1 Single Equation Methods
6.3.1.1 Instrumental Variables
We begin with Instrumental Variables (IV) estimation for several reasons. First, it
is easy to show that the estimator is consistent. Second, as we shall see, it is easy to
show that our other systems estimators are equivalent to the IV estimator. Third, the IV
estimator has a number of applications outside of systems models, making it rather more
general in applications.
Suppose that the jth equation is
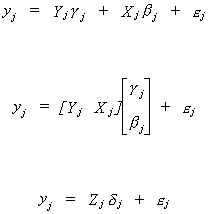
In an earlier section we showed that dj cannot
be consistently estimated because some of the variables on the RHS are correlated with the
error term. To get around this predicament we define Wj: Tx(mj+kj)
to satisfy
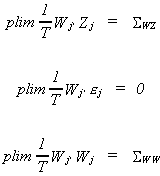
The IV estimator is
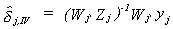
substituting for yj we get
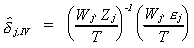
Applying Slutsky's Theorem we can see
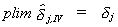
The asymptotic variance of the IV estimator (the variance of the asymptotic
distribution) is
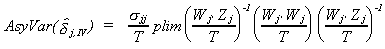
with

a consistent estimator.
Suppose that the system is exactly identified. Then
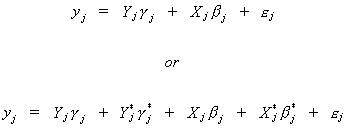
The * designates excluded variables. The number of excluded exogenous variables, kj*,
is equal to the number of included endogenous variables, mj. Let the matrix of
instruments be made from the included and excluded exogenous variables, W = [ Xj*
Xj ].
so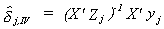 . Or, expanding the matrices
. Or, expanding the matrices
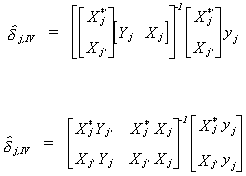
We can show the equivalence of the IV estimator and the Indirect Least Squares
estimator. Begin by going back and estimating the reduced forms coefficients for the
edogenous variables in the jth equation.
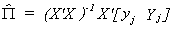
Premultiply by (X'X)
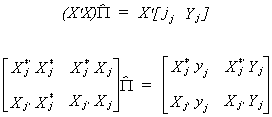 12 (a)
12 (a)
From our work on identification we know that the following restrictions must hold
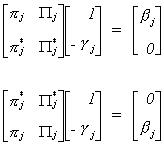
Now rewrite (a) as
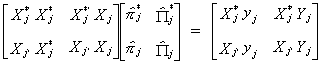
Postmultiply the above result by 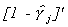 to
get
to
get
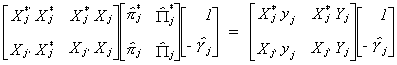
The product of the second and third matrices on the left hand side of the equation we
recognize as 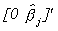 . Making this substitution
yields
. Making this substitution
yields
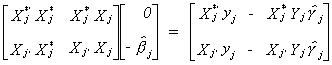
Doing the multiplication and rearranging terms gives the following
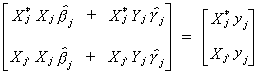
Now factor out the estimated parameter vector
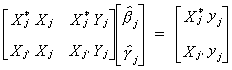 20 (i)
20 (i)
We can see that (a) and (i) are the same thing !
When the equation is overidentified ILS and IV are not equivalent. ILS produces more than one estimate of the
overidentified parameters, while IV uses the overidentifying restrictions in producing its
one estimate of each parameter.
What Does IV Do?
The following three figures help us understand what IV does. The first
figure shows the normal case of the classical regression model in which no RHS variable is
correlated with the error term. The second figure illustrates what happens when the zero
correlation assumption is violated but we apply OLS anyway. The third figure shows the IV
correction.
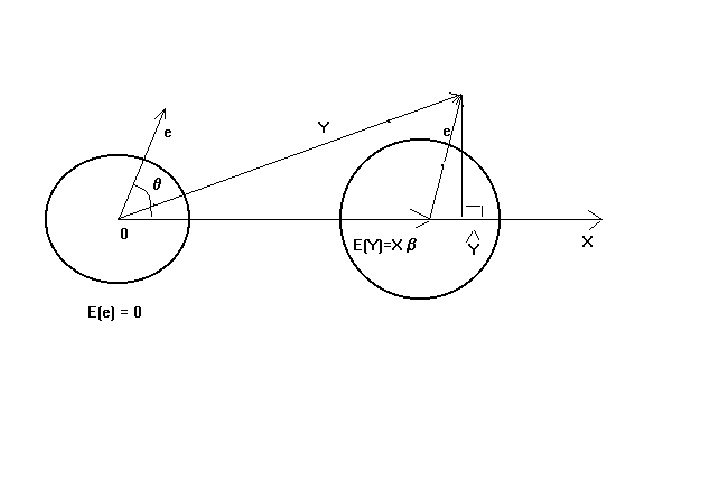
Figure 1: The Classical Regression Model
In the above figure Y is the dependent variable, X is the set of k independent
variables. The circles represent a contour of the normal distribution in the space in
which the dependent variable lies. The idea behind the contour is similar to the use of
indifference curves in micro theory. All the points on a contour are equally likely to
occur. Points on a smaller circle are more likely to occur; that is, they are higher on
the probability density function. e is a particular realization of the error term. The
particular realization of the error term is added to E(Y) to give the realized value of
the dependent variable. OLS then projects the realized dependent variable onto the space
spanned by the columns of X. Since the mean of the error term is zero, we are adding zero
on average to E(Y). On average then our OLS projection would give us E(Y) = Xb.
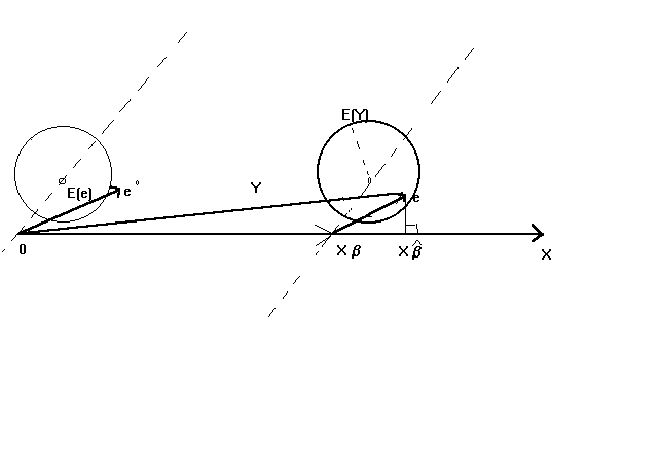
Figure 2: OLS When E(X'U)¹0
The principle difference between the first and second figures is that the mean of the
error term, conditional on X, is not zero. We have drawn it so that there is a positive
correlation between X and the error term. That is, the center of the error term contours
is no longer at the origin, nor is it the axis on which it lies at right angles to the
space spanned by X. Thus we are always adding a positive term to Xb.
The E(Y) is now located to the northeast of Xb. We will, on
average, be dropping a perpendicular from E(Y) onto the space spanned by X. As you can see
from the diagram we will overshoot Xb by some amount, even on
average. Our conclusion is that OLS produces biased estimates of the model parameters.
Increasing the sample size won't correct things since all we accomplish is to make the
contours tighter. Hence, OLS is also not consistent.
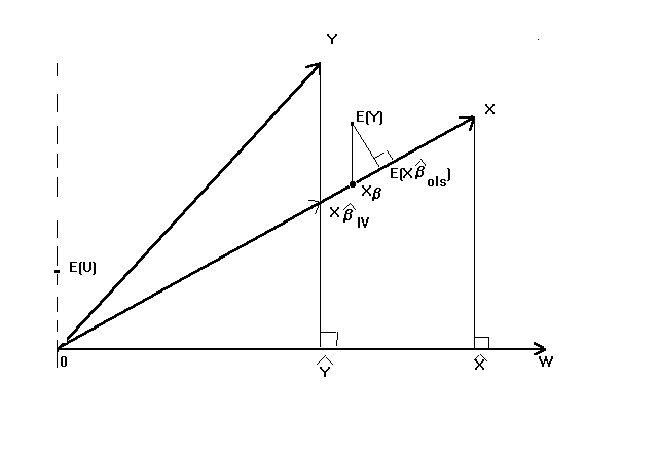
Figure 3: The Instrumental Variables Projection
In figure 3 the error contours have been suppressed to make the figure easier to
follow. The realization of the dependent variable, Y, is shown. As is the space spanned by
the 'independent' variables, X. The non-zero error term, correlated with the RHS
variables, is shown as before. The figure shows that E(Y) when projected orthogonally onto
the space spanned by the RHS variables couses us to overestimate Xb.
Added to the picture is the space spanned by the set of instruments.
IV first projects the RHS variables onto the space spanned by the instruments, W. Then the
dependent variable is projected onto this set of fitted values. As you can see from the
picture, when the dependent variable is projected onto W it results in an oblique
projection onto the original set of RHS variables. The result is that, at least in large
samples, we will correctly estimate Xb with greater likelihood.
The algebra is straightforward. We do the general case in which an equation is
overidientified because it provides a lead-in to the next section. We suppress the
subscript for the equation number.
Recall that Z is the full set of RHS variables, y is the dependent variable, and W is the
set of instruments. In the first step project the RHS variables onto the set of
instruments
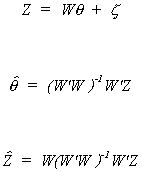
Replace the original RHS variables by their fitted values and estimate the original
set of parameters
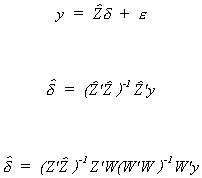
From the last line we can see that in IV we are really using a set of fitted values of
the dependent variable that have been created by projecting the dependent variable onto
the space spanned by the instrumental variables.
6.3.1.2 Two Stage Least Squares
We have the structural model
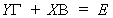 23 (i)
23 (i)
which can be written in reduced form as
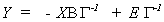 24 (ii)
24 (ii)
Our problem is that the system is overidentified. The consequence is that we cannot
use either ILS or the simple IV estimator outlined in the sections preceding the earlier
discussion of what IV does. We need to devise a method that uses all of the information in
the exogenous variables.
We will consider the jth equation
of (i)
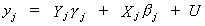 25
(iii)
25
(iii)
The usual problem is that Yj
is correlated with the error. IV solves this problem by choosing as instruments a set of
variables which are correlated with Yj,
but not with the error term. What we plan to do is use linear combinations of all the
exogenous variables in place of the endogenous variables which are included on the RHS of
the equation. To construct the linear combinations of the set of all exogenous variables
we run the regression
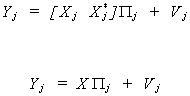
The fitted values of the included endogenous variables are given by
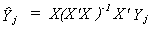
Note that (X'X)-1X'Yj is part of the matrix of reduced form
coefficients. With this result we can rewrite the model in (iii) as 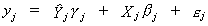 . After factoring out the coefficients we can
write this in matrix form as
. After factoring out the coefficients we can
write this in matrix form as
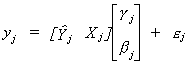
Now apply least squares
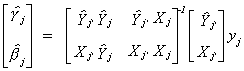
Now X(X'X)-1X' is idempotent so
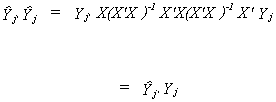
Since the exogenous variables are independent of the error term and the fitted
endogenous variables are orthogonal to the residual we can also write
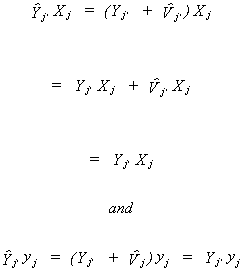
Making these substitutions, the Two Stage Least Squares estimator is

Suppose the model is exactly identified so that kj* = mj.
In this case Xj* would work equally well as the set of instruments
as 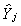 . If you go back to equation (i) on page
21 and make this substitution you will see that ILS, IV and 2SLS are all the same in the
exactly identified case.
. If you go back to equation (i) on page
21 and make this substitution you will see that ILS, IV and 2SLS are all the same in the
exactly identified case.
Finally, since the IV estimator is known to be consistent, we also know 2SLS to be
consistent.
6.3.1.3 Limited Information Maximum Likelihood
We are interested in the jth structural equation once again. We begin by
looking at a partitioning of the reduced form that corresponds to the jth
structural equation
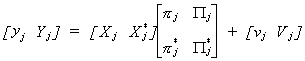
To economize on notation a little bit we will write this as
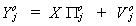
The error covariance matrix is written as
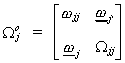
The log of the likelihood function for the joint density is
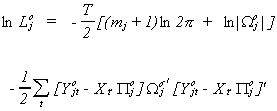
The idea is that we will maximize the likelihood for the equation of interest subject
to the constraints that we developed in the section on identification. Namely,
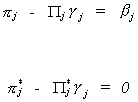
In the exactly identified case we can maximize the likelihood then go to the
constraints to solve for the structural coefficients. We conclude also that LIML is,
therefore, equivalent to ILS, IV, and 2SLS in the exactly identified case. Also observe
that the likelihood function is equivalent to that for the SUR model.
Returning to the over identified case, construct the concentrated likelihood function.
First, find
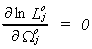
Solve for 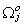 and substitute back into the
log likelihood, this will give us the likelihood in terms of only the reduced form
coefficients.
and substitute back into the
log likelihood, this will give us the likelihood in terms of only the reduced form
coefficients.
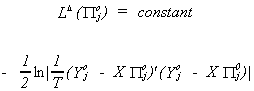
Now form the lagrangean
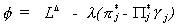
and determine
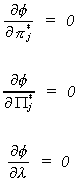
THEOREM
The LIML estimates for bj and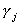 are respectively
are respectively
a) endogenous coefficients
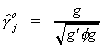
where the normalization rule is 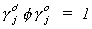 and g
is the solution to
and g
is the solution to 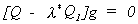 . In order for there to
be a solution the part in brackets must be singular. Therefore, l*
is found as the maximum root of the determinantal equation
. In order for there to
be a solution the part in brackets must be singular. Therefore, l*
is found as the maximum root of the determinantal equation 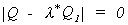 . So we conclude that g is the characteristic vector corresponding
to l*. Note that the root can be solved from
. So we conclude that g is the characteristic vector corresponding
to l*. Note that the root can be solved from 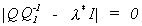 .
.
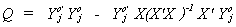
Q is an mj+1 x mj+1 matrix of RSS in the regression of all the
endogenous variables of equation j on all of the exogenous variables of the system.
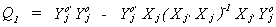
Q1 is an mj+1 x mj+1 matrix of RSS in the regression
of all the endogenous variables of equation j on only those exogenous variables included
in the jth equation.
b) exogenous coefficients
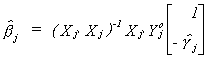
LEMMA
(i) 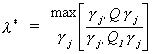
(ii) l* £ 1
Proof:
(i) Recall from linear algebra
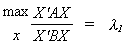
where l1 is the largest root of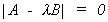
(ii) We can write Q1 = Q + D where D is a positive semi definite matrix. So
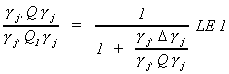
The Lemma leads us to a minimum variance ratio interpretation of the LIML. Consider
the jth structural equation in its original form and a version which includes
the entire set of exogenous variables
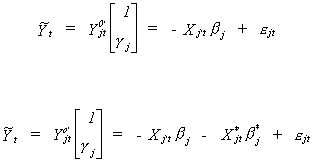
Incidentally, comparing these two specifications of the jth equation could
form the basis of a test for the exclusion restrictions of the structural model.
Define two sets of residual sums of squares corresponding to the two specifications of the
jth structural equation.
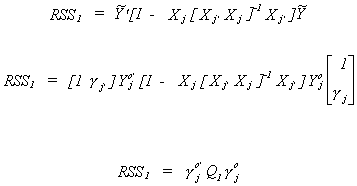
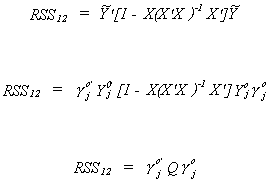
Now construct the ratio
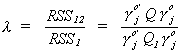
The trick is to pick the coefficients on the endogenous variables, 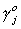 , so that l is
maximized. Or,
, so that l is
maximized. Or, 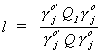 is minimized. Call this a
minimum variance ratio estimator
is minimized. Call this a
minimum variance ratio estimator
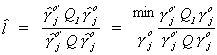
If 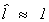 then we conclude that the exclusion
restrictions are correct. If
then we conclude that the exclusion
restrictions are correct. If 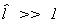 then we
conclude that the model is incorrectly specified. For any model
then we
conclude that the model is incorrectly specified. For any model 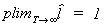 .
.
THEOREM
The LIML estimator minimizes the correlation coefficient between 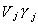 and Wbj*
and Wbj*
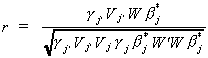
where Vj = Yj - Xj(Xj'Xj)-1Xj'Yj
is the residual from the regression of Yj on the included exogenous variables
and W = Xj*-Xj(Xj'Xj)-1Xj'Xj*
is the residual from the regression of the excluded exogenous variables on those which are
included. r is known as the cannonical correlation coefficient, so LIML is also known as
the minimum correlation coefficient estimator.
6.3.1.4 k-Class Estimators
Consider first the 2SLS estimator
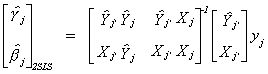
Which we can rewrite as
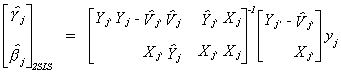
If we had applied OLS to the model we would get
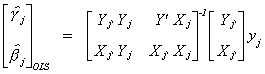
If we construct an estimator
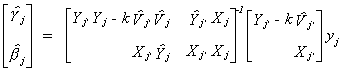
then one can see that when k=0 we get OLS and when k=1 we get 2SLS.
THEOREM
Recall that we had previously said that LIML was the minimum variance ratio
estimator
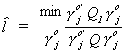
If we let k = 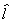 in our k-class estimator
then we get the LIML.
in our k-class estimator
then we get the LIML.
Proof:
Recall
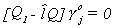 76 (1)
76 (1)
To solve for 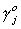 we will partition Q1 and Q as Q1 = [q11 Q12]
and
we will partition Q1 and Q as Q1 = [q11 Q12]
and
Q = [q1 Q2], where q11 and q1 each
have one column corresponding to the endogenous variable on the left hand side of the
structural equation, and Q12 and Q2 each have the
remaining mj columns for the other included endogenous variables of the
equation. This allows us to rewrite (1) as
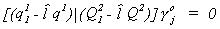
There are mj + 1 equations in this system; we have one too many so need to
discard one. We can partition further as
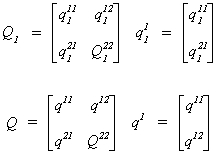
Given our definition 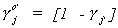 , we can use our
partitioning to disregard the first equation in the determinantal equation and use
, we can use our
partitioning to disregard the first equation in the determinantal equation and use
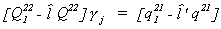
Rearranging, we can derive the LIML estimator
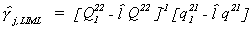
Now suppose that there are no included exogenous variables. That is, kj = 0
so
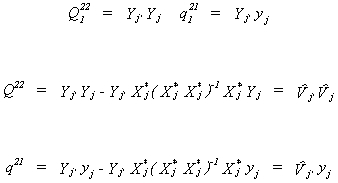
Note that we have Xj* in both Q22 and q21 because there is no difference between the
set of all exogenous variables and the set of all excluded exogenous variables for this
particular example. Substituting into 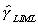 we
get
we
get
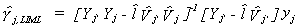
We conclude then that the LIML estimator is also a k class estimator.
There is a problem with the k-class estimator
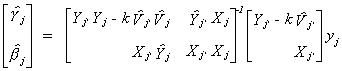
for some value of k the inverse explodes, so we get the follwoing relationship between
the different estimators. We know that the k for LIML is always greater than 1. Therefore,
the diagrams show us the ordering for the estimates, always!
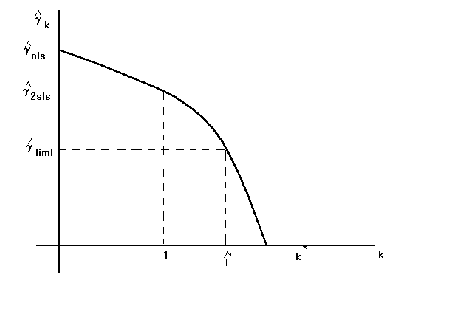
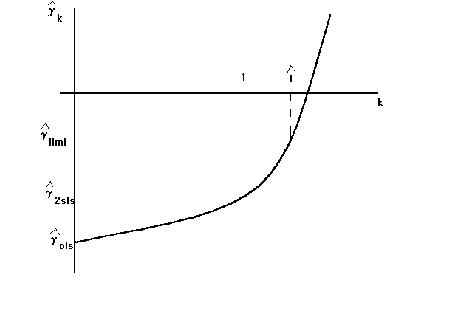
6.3.2 System Methods
6.3.2.1 Three Stage Least Squares
The first equation of the structural model is
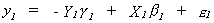
Or, using the notation we adopted for our explorations of 2SLS
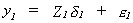
In general we can write the jth equation in the system as
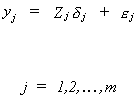
Now we will put the equations together as we did for SURE. Toward that end define the
following vectors and matrices
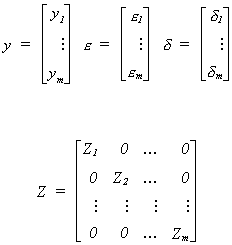
So the whole system can be written as
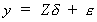 5 (1)
5 (1)
Premultiply (1) by 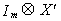 , where X' is the
kxT matrix of all observations on all of the exogenous variables.
, where X' is the
kxT matrix of all observations on all of the exogenous variables.
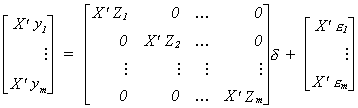 7 (2)
7 (2)
Rewrite (2) as
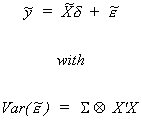 8 (3)
8 (3)
Estimate the coefficients of (3) by GLS
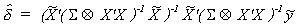 9 (4)
9 (4)
Estimate S as follows
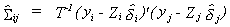 10 (5)
10 (5)
where 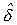 is the 2SLS estimate. Substitute
(5) into (4) to get the 3SLS estimate.
is the 2SLS estimate. Substitute
(5) into (4) to get the 3SLS estimate.
6.3.2.2 Full Information Maximum Likelihood The complete system of m
structural equations is written
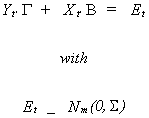
Using all of the observations
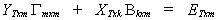
where the subscripts show the dimensions of the matrices. The likelihood function is 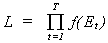 . Using a theorem form distribution theory we
can rewrite the likelihood as
. Using a theorem form distribution theory we
can rewrite the likelihood as
The term at the right end of the expression is the absolute value of the determinant of
the matrix of partial derivatives. You wil recognize this as the Jacobean of the
transformation. In this instance it is given by 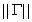 so the likelihood is
so the likelihood is
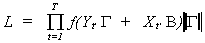
Substituting in for the normal density
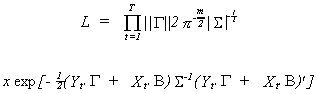
As usual it is easier to work with the log likelihood. We will also make use of the
fact that the exponent is a scalar. As such, taking its trace has no effect.
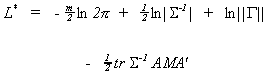
where
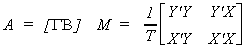
We have the following factoids from linear algebra
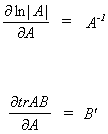
First consider
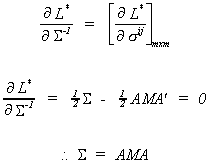
Substituting back into L* gives us the concentrated likelihood function.
The likelihood function is concentrated in the sense that we have found a maximum in the
G(G+1)/2 hyperplane of the covariance parameter space.
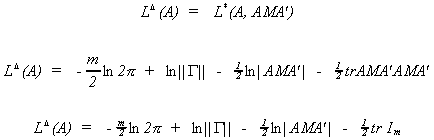
The result of substituting back in for AMA' gives
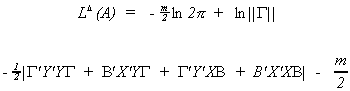
One would proceed by differentiating this with respect to the unknown coefficients,
setting those partials to zero and solving. Needless to say, the first order conditions
would be highly nonlinear. For years this was the stopping place in Full Information
Maximum Likelihood. With the advent of cheap computing power, it became possible to write
hill climbing algorithms based on the Gauss Newton principle that could solve these
equations numerically. That is, in fact, how LIMDEP, RATS and TSP do their maximum
likelihood estimation.
Before moving on, it is worth considering the exactly identified case. Go back to the
original likelihood and substitute in the reduced form 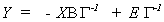 to get
to get
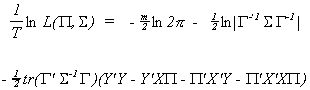
Define
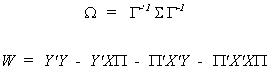
and write the likelihood function as
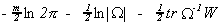
The first order condition for the maximum is
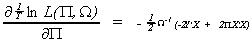
From the FOCs we can derive estimates of the reduced form parameters 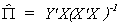 . Therefore, we conclude that in the exactly
identified case, OLS provides us with the maximum likelihood estimates of the reduced form
parameters. We could then solve the reduced form parameter equations for the structural
parameter estimates.
. Therefore, we conclude that in the exactly
identified case, OLS provides us with the maximum likelihood estimates of the reduced form
parameters. We could then solve the reduced form parameter equations for the structural
parameter estimates.
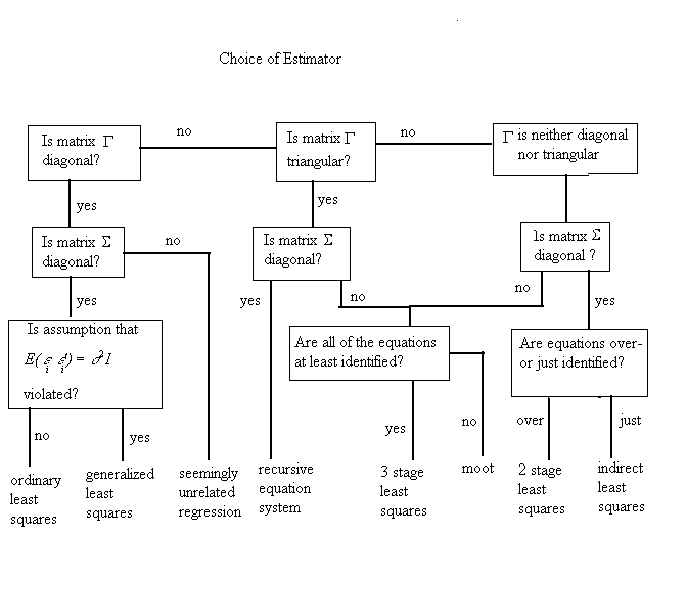
To picture the relationship between estimators I have provided the following flowchart.
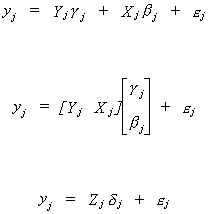
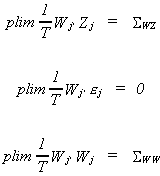
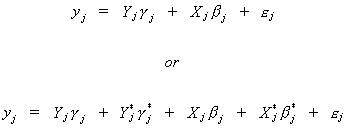
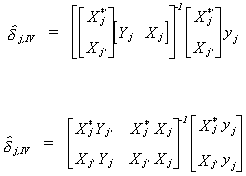
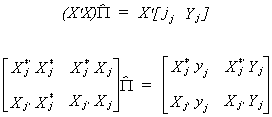 12 (a)
12 (a)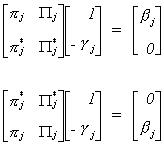
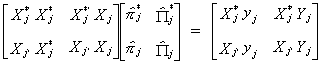
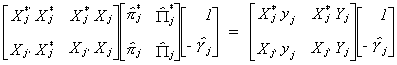
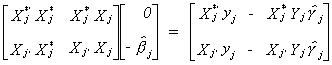
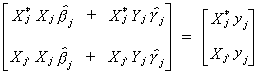
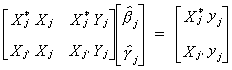 20 (i)
20 (i)


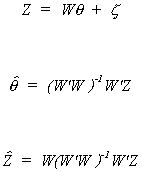
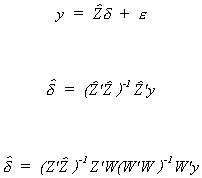
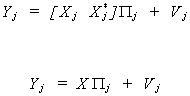
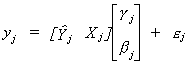
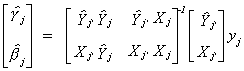
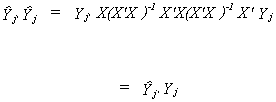
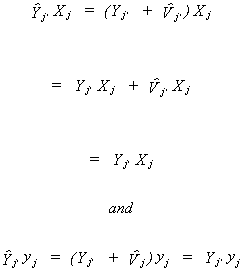

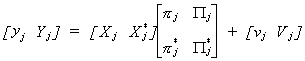
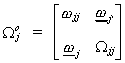
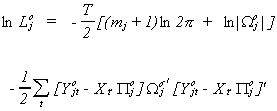
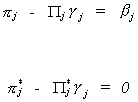
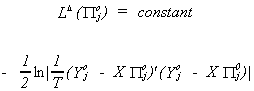
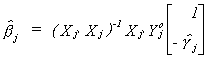
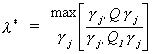
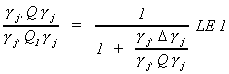
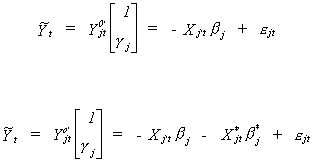
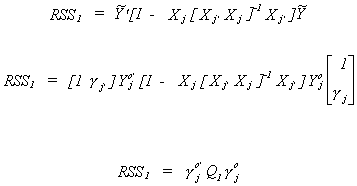
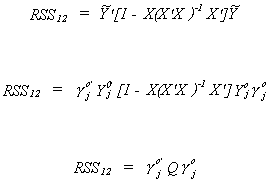
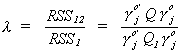
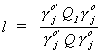 is minimized. Call this a
minimum variance ratio estimator
is minimized. Call this a
minimum variance ratio estimator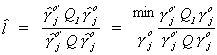
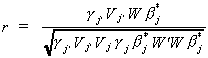
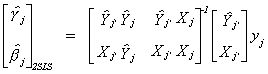
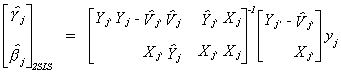
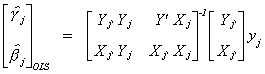
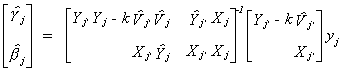
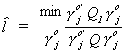
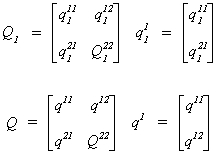
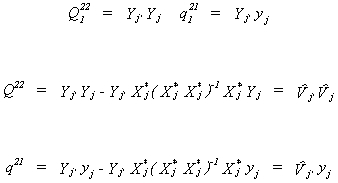
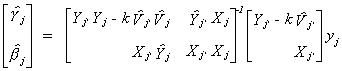
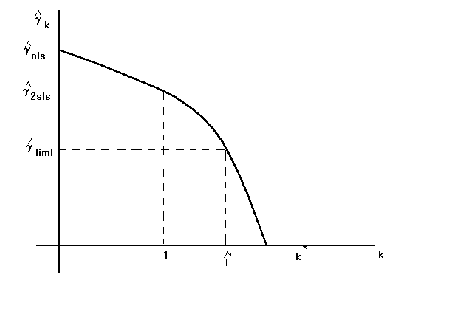
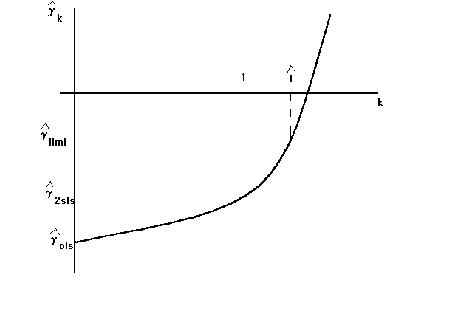
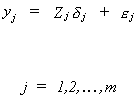
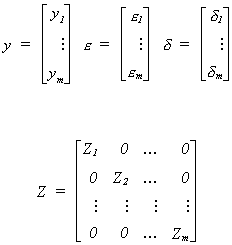
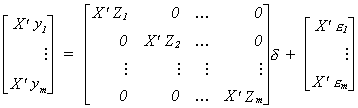 7 (2)
7 (2)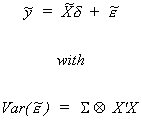 8 (3)
8 (3)