System Estimation: An Example

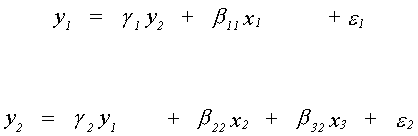
6.3.3 An Example of Systems Estimation
The following model is specified

All variables are specified as deviations from their means, that's why there is not an intercept in either equation. Using the order condition, the first equation is overidentified. The second is exactly identified. Can you work out the rank condition for each equation?
The sample of observations produces the following matrix of sums of squares and cross products.
y₁ y₂ x₁ x₂ x₃20 6 4 3 5 y₁6 10 3 6 7 y₂4 3 5 2 3 x₁3 6 2 10 8 x₂5 7 3 8 15 x₃One reads the table in the following fashion. To find the sum of products of a pair of variables, read into the table from the appropriate row and column. For example,

The OLS estimates are:

These estimates are not unbiased and are not consistent. In order to achieve the latter property we can use 2SLS. These results follow: Look at the OLS estimator. Everywhere you see an endogenous variable on the RHS it must be replaced by its fitted value. First we need the total sum of squares for the fitted vector y₂

Now compute the product of the fitted vector y₂ and the dependent variable of the first equation, y₁.

Now compute the total sum of squares for the fitted values of y₁ for use in our estimates of the coefficients of the second equation

Now the product of the vector of fitted values for y₁ and the actual values of y₂

Putting the pieces together we get the 2SLS estimates of the coefficient vectors.

The asymptotic covariance matrices are found from the following steps: First compute estimates of the error variance for each structural equation

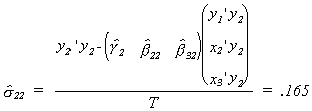
Now compute the covariance matrix for each coefficient vector

For later use we will also compute the error covariance between equations

The Limited Information Maximum Likelihood estimates are computed following the last theorem of section 6.3.1. For the first equation the first step is to calculate the matrices of sums of squares. First compute Q₁²², the residual sum of squares from the regression of the right hand side endogenous variable on the included exogenous variables, and q₁²¹, the product of the residuals from the regression of y₁ on the included exogenous variables and the residuals from the regression of y₂ on the included exogenous variables.

Now calculate Q²², the residual sum of squares from the regression of the right hand side endogenous variable on the entire set of exogenous variables

Now calculate q²¹, the product of the residuals from the regression of y₁ on the complete set of exogenous variables and the residuals from the regression of y₂ on the complete set of exogenous variables.

We need to find the smallest root from the ratio of two quadratic forms; two variances. First find Q, the RSS and cross equation sums of squares from the regression of both y₁ and y₂ on the entire set of exogenous variables

Finally, Q₁ is the set of RSS and cross sums of squares from the regression of y₁ and y₂ on only those exogenous variables included in the equation of interest.

Now use Q^-1 and Q₁ to compute the necessary eigen values.

Using the roots and the pieces from the partitioned Q and Q₁ we can solve for the coefficients on the endogenous variables

The coefficients on the exogenous variables are

For the second equation we repeat the process.
First compute Q₁²², the residual sum of squares from the regression of the right hand side endogenous variable on the included exogenous variables, and q₁²¹, the product of the residuals from the regression of y₁ on the included exogenous variables and the residuals from the regression of y₂ on the included exogenous variables.

Now calculate Q²², the residual sum of squares from the regression of the right hand side endogenous variable on the entire set of exogenous variables

We need to find the smallest root from the ratio of two quadratic forms; variances. Since this is the same as the first equation we need not do it again.
Using the roots and the pieces from the partitioned Q and Q₁ we can solve for the coefficients on the endogenous variables

The coefficients on the exogenous variables are

We can collect all of the single equation estimates in a table

		b₁₁		b₂₂	b₃₂
OLS	.439	.537	.193	.384	.197
2SLS	.369	.579	.484	.367	.109
LIML	.367	.58	.508	.366	.102

Note the ordering of the coefficient magnitudes as you read down the columns. Given the earlier graphs, we expected to see this result.

Now let us calculate the three stage least squares results. First define the estimate of the error covariance matrix for the system of equations as

We will use the inverse of this covariance matrix in the construction of this asymptotically efficient estimator. To economize on notation somewhat we will use, for example, s¹¹ to represent the row 1 column 1 element from this inverse. Since the matrices involved are quite cumbersome, we'll do the computations in two pieces. First do the computations for the part which needs to be inverted

After A is inverted it is post-multiplied by

Now d_3sls = A^-1B, or

Except for some rounding errors, the 2SLS and 3SLS results are the same. You, of course, expected this. The 3SLS is an efficient version of the 2SLS estimator. You encountered a similar type of result when you worked with SUR in an earlier chapter.
6.4 Aspects and Properties of the Estimators

1. All the estimators we have looked at are IV estimators. The principle differences are: a) choice of instruments and b) some of the estimators estimate all of the coefficients jointly.
2. For the exactly identified case, indirect least squares is consistent and efficient. When the equation is exactly identified ILS and 2SLS are equivalent methods.
3. In the overidentified case 2SLS is a consistent estimator and is asymptotically efficient. For well behaved data, the CLT can be used to show convergence in distribution to the normal.
4. For the k-class estmators we know plim(k) = 1. Therefore, they are consistent and all have the same asymptotic covariance. This is true for 2SLS and LIML, so both are efficient in the class of single equation methods.
5. Iteration of the 3SLS estimator does not provide the maximum likelihood estimator, nor does it improve asymptotic efficiency.
6. Since 3SLS is an IV estimator, it is also consistent. Among all IV estimators, 3SLS is efficient. For normally distributed error terms 3SLS has the same asymptotic distribution as FIML.
7. As a maximum likelihood estimator, FIML is asymptotically efficient among systems estimators. We also know it to be an IV estimator, of the same form as 3SLS.
8. Asymptotically 2SLS must dominate OLS, in spite of what might be observed in small samples.
9. In a correctly specified model, a full information estimator must dominate a limited information estimator.
10. Systems estimators will propagate misspecification errors throughthe entire model.
11. In finite samples the estimated covariances of the estimator can be as large for a system estimator as for a single equation method.
12. There are some small sample monte carlo results which suggest the following:
a. If the endogenous variables are strongly jointly determined, then 2SLS and LIML are more highly concentrated around the true parameter.
b. Even though 2SLS is consistent, its small sample bias is not negligible.
c. In small samples, OLS tends to have the smallest variance.
d. 2SLS has a larger bias than LIML, but tends to have a smaller sampling variance.
e. In empirical work the LIML tends to explode. This is due to the fact that its small ample distribtution has fat tails. Intuitively, this is an expected result given the earlier figures concerning the k-class estimators.
f. Among the k-class estimators, the optimal value of k appears to be between .8 and .9.
g. LIML is median unbiased and its distribution is more symmetric than that for 2SLS.
h. Since OLS is seriously biased and LIML tneds to be greatly dispersed, 2SLS is the estimator of choice.

6.5 Specification Tests

6.5.1 Exclusion Restrictions
We are considering the following test of hypothesis
H_o: the exclusion restrictions are correct
H₁: the exclusion restrictions are not correct
Single Equation Tests
1. Anderson and Rubin

where lambda is the smallest root from the LIML estimation routine. This test statistic, which is a large sample test, has the drawback that it rejects the null too often.
2. Basmann
a. His first test is based on the 2SLS estimates of the endogenous coefficients in the j^th equation.

b. His second test is based on the smallest root from the LIML estimator

3. Hausman

where the R² is from the regression

<

The term between the equal signs is the set of residuals from estimating the jth equation by 2SLS. This is just another variant of the Hausman test we have seen before. It is driven by the notion of specification error. If the exogenous variables are inadvertantly excluded then the resulting estimator is not consistent. The test statistic is comparing what happens to the coefficients on the included variables with and without the exclusion restrictions.
System Test
The Full information estimates in this test can be either FIML or 3SLS.

6.5.2 Endogeneity
The test developed by Hausman which we used for distinguishing between the fixed effects and random effects models is applicable here. As in that case, the test statistic is driven by misspecification. We are given a choice between an estimator which treats a variable(s) as exogenous and one which treats it (them) as endogenous.
Begin by specifying the null and alternate hypotheses
H_o: The model is correctly specified. The RHS variables are uncorrelated with the error term. Both estimators are consistent, one of them is efficient.

H₁: Model is not correctly specified. One estimator is not consistent.
Consider the j^th equation:

where X^* is an included variable that we believe to be exogenous. Rewrite the equation as

Define as the 2SLS estimator treating X^* as exogenous and included.
as the IV estimator when X^* is treated as an included endogenous variable.
The Wald test statistic is

The number of degrees of freedom is equal to the column dimension of X^*