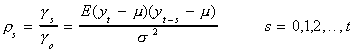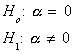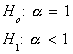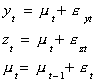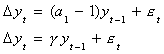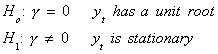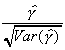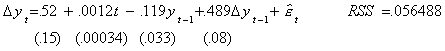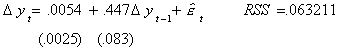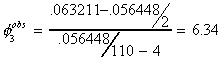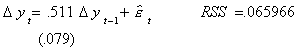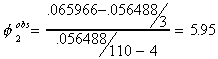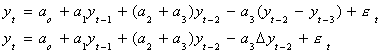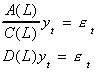Testing for Unit Roots

Time series analysis is about the identification, estimation and diagnostic checking of stationary time series. By way of review we offer the following definitions:

Definition: The sequence {yt} is said to be covariance stationary if for all t and t-s

1. E(y_t)= E(y_s)= m
2. E(y_t-m)² = E(y_t-s-m)² = s²
3. E(y_t-m)(y_t-s-m) = E(y_t-j-m)(y_t-j-s-m) = g_s
   

That is, the mean, variance and covariance are invariant to the time origin.

Definition: Suppose we have the sequence {y_t} (t=0,1,2,…) with mean m and variance s². Then the autocorrelation function or correlogram is given by




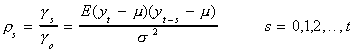
Suppose we have a series {y_t} which we know to have been generated by an AR(1) process, say,



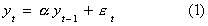
where 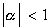and e_t is white noise. We can estimate the parameters in (1) by OLS: Our estimator is efficient and the series is stationary since 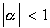. We could use a t-statistic to test the hypothesis



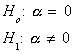
This is a legitimate test since the null is a refutable hypothesis, even though the power against a local alternate is negligible.
But suppose that the data was really generated by

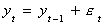
Upon recursive substitution this can be rewritten as

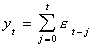
which is nonstationary since 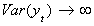as t gets large. Now we would want to test

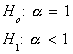
There is a problem, however, since the center of mass of the usual estimator would be bounded away from 1. We would tend to err on the side of rejecting too many H_{0 .} The question of the presence of a unit root is particularly problematic in regression models of the sort

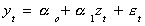
We usually assume that {y_t} and {z_t} are both stationary and that e_t is white noise. If the two variables are nonstationary then we will likely get spurious results: high R² and statistically significant coefficients even though there may not really be a meaningful relationship between y and z. There are four cases to consider

1. Both {y_t}and {z_t} are stationary and the classical regression model is o.k.
2. The sequences {y_t} and {z_t} are integrated of different orders. Regression models containing such nonstationary series are meaningless.
3. The nonstationary {y_t} and {z_t} are both integrate of order 1, say, and the error term has a stochastic drift. Now all errors are permanent. That is E_te_t+i = e_t . But we can apply OLS with good effect to
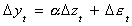
4. {y_t} and {z_t} are integrate of the same order and the residual sequence is stationary. Then {y_t} and {z_t} are said to be cointegrated. For example:

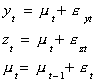
Both {y_t} and {z_t} are unit root processes but y_t-z_t = e_yt-e_zt is stationary. We will leave case 4 until the chapter on cointegration. For now we will concern ourselves with determining whether or not the series {y_t} has a unit root.

Dickey-Fuller Tests

Consider the data generating process



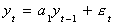
And the associated question, is a₁ = 1? Subtract y _t-1 from both sides to get



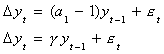
g=0 implies a₁=1 implies a unit root in {y_t}.

We can allow for drift by including an intercept



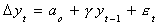
Definition: The term stochastic drift comes from the following: Suppose that the process is



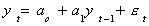
We can rewrite this as



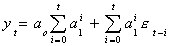
In the next period, i.e. t+1, the intercept is a_oa₁^t+1 larger, to which we add a stochastic term. We have seen this idea of a stochastic intercept elsewhere. Namely in the random effects model.

We can allow for a linear trend with drift



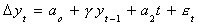
In any event, our test of hypothesis is

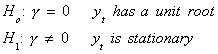
The test statistic we use for the test of hypothesis is constructed as a t-statistic. That is

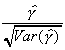
The critical values come from a set of tables prepared by Dickey and Fuller. The tables were generated empirically. We are accustomed to doing tests with critical values we have determined analytically by integration of a known distribution function.

The particular table to be used depends on whether the model has an intercept or a trend in it. However, the critical values are not changed by including terms on the right hand side.


To guide you in the testing procedure, consider the following flow diagram from Walter Enders, Applied Econometric Time Series, Wiley, 1995.

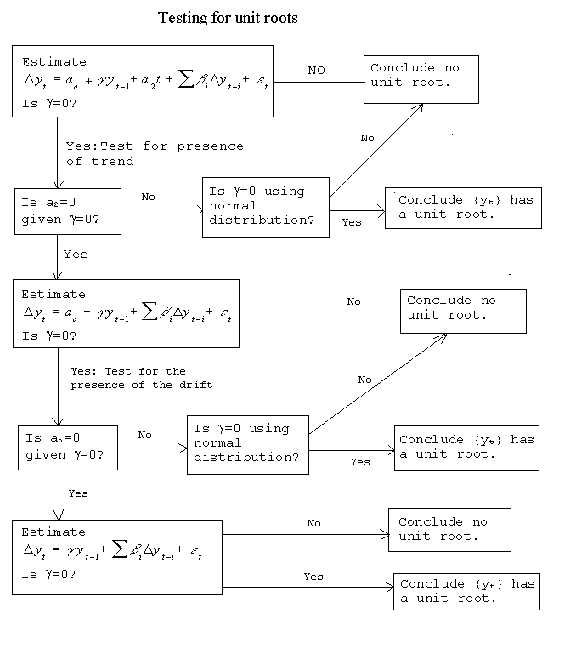
One starts in the top left corner with the most general model, that includes a stochastic drift and a deterministic trend. Either the trend or the drift can produce the appearance of a unit root in their own right, so they must be included at the outset. Recall that an excluded relevant variable introduces bias, but an included irrlevant variable only has a cost in terms of efficiency. If the null of a root is not rejected, then proceed by testing for the significance of the trend term in the presence of a unit root. If the trend term is not significant, then test for the significance of the drift term. If along the way we find that either the trend or the drift is not zero then we proceed immediately to to test for the significance of g.


Example

The following models have been fit to the Federal Reserve Bank production index for the period 1950:1 - 1977:4, a total of 112 observations. In all three models the numbers in parentheses are standard errors. The most general mode, corresponding to the start of the flow diagram is

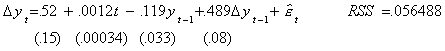
At the 5% level of test (2.5% in each tail) the critical value for the coefficient on y_t-1 for a model with drift and trend is -3.73, compared to an observed test statistic of 3.6, so we fail to reject the null. For the moment we believe there to be a unit root. Next we fit a model which imposes the restriction that g=0, and test to see if the trend coefficient is zero. Note that on the basis of a conventional t-test, the trend coefficient is highly significant.
A model with drift but no trend and which supposes that there is a unit root is

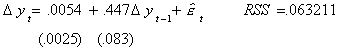
Now the test of hypothesis is

H_o: unit root, no trend
H₁: one or both not true

The appropriate test statistic is constructed as though it was an F-test, but the critical value is read from a different set of tables.



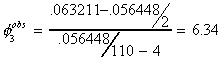
The critical value at the 5% level is 6.49, so we fail to reject the null. Our conclusion to this point is that there is a unit root and that the trend should be excluded.


A model with neither drift nor trend, but which presumes a unit root is

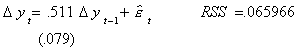
The test of hypothesis is

H_o: unit root, no trend, no drift
H₁: one or more belongs

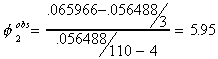
The critical value at the 1% level of test is 6.50. Since our observed test statistic is smaller than the critical value, we fail to reject the null. Our conclusion is that there is a unit root, there is neither trend nor drift.

Extension of Dickey-Fuller

Suppose that the data generating process is

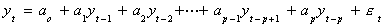
This is quite a bit more general than the process we started with. It will also admit a multiplicity of roots. We need to augment Dickey-Fuller in order to test for this possibility. Let us consider the AR(3) process



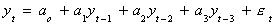
We will add and subtract a₃y_t-2 to get



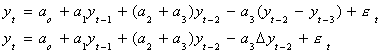
Now add and subtract (a₂+a₃)y_t-1 to get





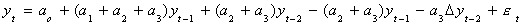
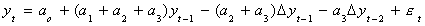
Finally, subtract y_t-1 from both sides

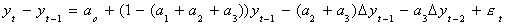
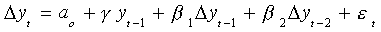
Now we can test for the presence of a unit root. We know that if the coefficients in a difference equation sum to one then at least one root is unity. In the present context this amounts to testing g=0, as in the simpler case. The critical values for this augmented model remain the same as before. Parenthetically, adding a time trend causes a headache when it comes time to derive the large sample properties of the OLS estimator since x'x will no longer be finite element-wise.

Problems with D-F and augmented D-F

1. The error term may have a moving average term in it.

Suppose A(L)y_t=C(L)e_t and the roots of C(L) all lie outside the unit circle so C(L) is invertible. Then

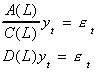
Unfortunately D(L) will be of infinite order, but we can use our earlier procedure
to write



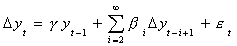
With our finite data sets we might be in trouble if not for the fact that it has
been shown empirically that a good approximation will cut off the distributed lag
at the T/3 term.

1. 2. What is the appropriate lag length for the differenced terms included on the RHS?

The problem of too many lags reduces the efficiency of the estimator. This is
a much less serious problem than using too few lags. As pointed out before,
excluding relevant variables will affect the bias and consistency of the OLS
estimator.

3. DF tests to see if there is at least one root. Suppose there are more?

For example, one could estimate the parameters of the model
(1-L)²y_t = b₁(1-L)y_t-1 + e_t . One would then use the DF statistics, as appropriate
to the case, to test b₁ = 0. If b1=0 then there are 2 unit roots, if it is not
zero then one must go on and test to see if there is a single unit root.
The procedure is generalized in the obvious way.

4. How do we know which deterministic regressors belong in the model?

The procedures used in the FRB production example and in problems 2 and 3 use
cascading tests of hypothesis. As is shown in Theil, Principles of Econometrics, Wiley, 1971, this reduces the purported significance level of the test in each succeeding step. Along the same lines, Judge and his numerous coauthors would argue that the procedure outlined in the flow chart puts in the realm of pretesting and hence higher squared error loss over a large part of the parameter space. Nonetheless, in applied work we often disregard these caveats and use the process in the flow chart.

Another Example: Purchasing Power Parity

Under PPP, the rate of currency depreciation is approximately equal to the difference between the domestic and foreign inflation rates. The PPP model implies

e_t= p_t - p^*_t + d_t

where p_t = log of the US price level
p^*_t = log of the foreign price level
e_t = log of the dollar price of foreign exchange
d_t = deviation from PPP at time t

The three data series apply the log transformation so that we are using inflation rates.

In certain PPP models it is possible for real shocks to either demand or supply to cause permanent deviations. Intuitively the deviations should not persist or there would be substantial opportunities for profit taking. And anyway such profit taking and arbitrage would restore PPP eventually. A popular procedure in the empirical modeling of PPP is to construct the series

r_t = e_t + p_t^* - p_t

If PPP is to hold then r_t must be stationary with a zero mean. Furthermore there can be neither trend nor stochastic drift. To digress and anticipate the material in another section, e_t, p_t and p^*_t are said to be cointegrated when the PPP model is true. This specific formulation of the model imposes a specific cointegrating vector on the three variables.

Fit the model



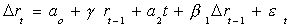
to monthly data for the pre- (1960.1 - 1971.4, T=136) and post- (1973.1 - 1986.11, T=167) Bretton Woods eras to get the following results, with coefficient standard errors in parentheses:

g

a0

a2

SD

SEE

t

1973-86

-.047
(.074)

1.25

-.297

10.44

2.81

-.63

1960-71

-.030
(.028)

.97

.017

.005

-1.04

1. Note that a₂ =0 for the latter period. This reason alone calls into question the validity of the PPP.
2. In neither period can we reject the null of a unit root. The observed t is small by any standard.
3. The change in exchange rate regime has made exchange rates more volatile and unpredictable (see the SD and SEE).

In this example we fail to reject the null of a unit root. We cannot believe in the PPP model. But our testing procedure is predicated on the constant variance of the error term, which does not appear to be the case.

Phillips and Perron have devised corrected test statistics for the instances in which the error is an MA, is perhaps heterogeneous, or there is a structural break in the data.

Structural Change

How can we tell the difference between a series which has a structural break in it, but would otherwise be stationary, and a series which is not stationary, but which due to an impulse seems to evolve like the first series?
Consider a model in which there is a shift in the intercept


y_t = .5 y_t-1 + e_t + D_L

where D_L is one for many consecutive periods and zero otherwise. An example is the following figure.

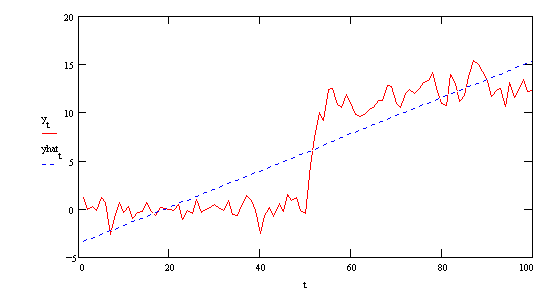
The red line is the original series. The blue line is the simple regression of y_t on time (a=-3.543, b=.189). In the regression of y_t on y_t-1 we get

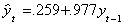
Apparently the structural break causes the coefficient on y_t-1 to be biased toward one. For all appearances y_t is not stationary, although we know it to be stationary both before and after the break at t=50. Even without doing the test for this case, we would not expect Dickey-Fuller to be very robust against these models with a structural break in them. Indeed the observed test statistic is t=.507

Now consider a non-stationary model in which there has been a once and done pulse


y_t = y_t-1 + e_t + D_P

where D_P is one in a given period and zero otherwise? An example is in the following figure:


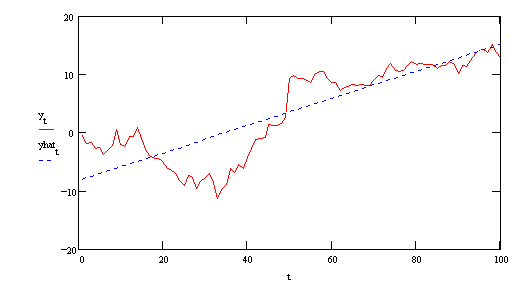
The red line is the original series. The blue line is the simple regression of y_t on time (a=-8.086, b=.233). There is an apparent break at t=50. The regression of y_t on its lagged value gives us

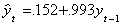
Even without a formal test, the size of the coefficient leads us to suspect a unit root, which is indeed the case. Without a statistical test we really cannot distinguish this case from the prior instance.

Phillips and Perron have developed a test for this problem. Consider the working model



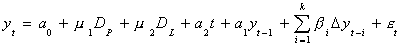
in which D_P is a pulse equal to one in a period and zero otherwise, D_L is one for some consecutive periods and zero otherwise.

Step 1. Estimate the coefficients of the full model.

Step 2. Compare the t-statistics to the critical values in Perron. Of particular interest will be the coefficient a₁.

When Perron used this method to analyze the Plosser-Nelson data he found that most macro time series are trend stationary.