Governor Tom Ridge is seeking new sources of revenue for funding new initiatives. Pennsylvanians have a business, the stores of the Pennsylvania Liquor Control Board, they think they may want to sell in order to help the Governor pay for his initiatives. In private industry this would present no special difficulty. Business owners in the private sector work with an accountant, a lawyer, and a business broker to value the firm fairly and market the business. Those involved will look at the profitability of the firm, the profitability of competitors and the opportunities for growth. The business broker finds a buyer with the requisite qualifications. The seller and buyer bargain over the asking price. If everyone has done their job, then the seller can be fairly confident that the price he receives will be very close to the value of the firm to the new owner.

The business Pennsylvanians think they want to sell has never been operated in the private sector in their state. Within the state there are no private sector counterparts against which to compare the business for the purpose of valuation. The owners of the business, all of the residents of the Commonwealth, are so widely dispersed that management, composed of career civil servants, has been able to set its own agenda. Such behavior is consistent with economic theory. That agenda may or may not have been profit maximization. This compounds the valuation problem. There is no assurance that if the business is sold in the conventional manner that the Commonwealth will receive a price close to its value to the new owners.

In surveying the market for businesses, goods and services, a common feature stands out. When goods are not standardized, when the intrinsic value of the good is uncertain, or when the market clearing prices are highly unstable, posted prices work poorly, and auctions are usually preferred (McAfee and Preston, 1987).

In the private sector there are many goods whose intrinsic value is uncertain, but which are traded every day. Wines are auctioned regularly in California, New York, and in the major cities of Europe. The wines at auction are not always rare, aged vintages with a known historical quality. New vintages, which may not be consumed for years, are also sold at auction. The buyers try to value the new vintages prospectively on the basis of their knowledge of weather during the growing season and the future of wine drinkers' preferences for varietals of a given type.

Government bonds are auctioned every week in many countries of the world. Their present value depends on the uncertain course of future interest rates and exchange rates. Different individuals forecast the future of interest rates differently, so those bonds have different values to each person in the market. If the government were to set a fixed take-it-or-leave-it price, the way brooms are sold at Home Depot, they could not know whether they have gotten the best (highest) possible price.

National governments around the world have used auctions to sell 'commodities' which are being brought to the market for the first time. In these cases the government cannot possibly know how the business community will value the good. The U.S., Australia and New Zealand have all used auctions to sell the rights to radio, TV, and telephone signals on different bands of the magnetic spectrum.

This paper proposes the use of an auction to transfer the rights to the retail distribution of wine and liquor in Pennsylvania. In the next section we briefly reprise the case for privatization. We then survey the theory of auctions and their design. The West Virginia experience is reviewed and used to develop an empirical model for valuing the likely price to be fetched by the Pennsylvania system. Concluding remarks include recommendations for auction procedures and a forecast of the results of such an auction.

The Case for Privatization

In posing the question of whether the state should privatize liquor and wine distribution, one should first consider the working premises of those opposing such a move. The first one seems to be that alcohol consumption is intrinsically bad for the individual and society. It cannot be denied that there are adverse health consequences from the excess intake of alcohol. The individual tales of the personal costs of alcohol abuse are sad and compelling. At the same time, there are only a handful of countries around the world which are willing to incur the incremental cost of total prohibition in order to save a small minority from the costs of their abuse. Societies in the rest of the world rely on different degrees of government control and private distribution to make alcohol beverages available. The reason for this is quite simple. There is just no easily interpreted empirical evidence to suggest that private distribution is more damaging to the public weal than government monopoly.

Since alcohol beverages are made available to the public, the obvious follow on question is the prevention of alcohol abuse and the consequent drunk driving, violence and work related injury. Addressing this issue is an industry in itself, with its own foundations, working groups and journals. Nowhere in the alcohol beverage literature is it widely concluded that government ownership of the alcohol beverage distribution system is a necessary adjunct of the regulation of consumption (Holder, 1993).

Over the last decade Iowa, West Virginia and Alberta, Canada have all privatized some or all of their alcohol distribution system. To one degree or another all three of them recognized the disciplinary force of the private sector as the best way to promote economic efficiency. The private sector could be relied upon to locate retail outlets in desirable locations, to stock stores with products desired by consumers, and to charge prices reflecting demand in the market. It was also recognized that privatization would be a direct way to promote entrepreneurship in the state or province. Privatization was seen as a way to increase public revenues through the periodic sale of licenses and recurring sales tax revenues. In many respects, all of these goals have been met.

In Alberta where taxes are excise based, retail prices have fallen on high end items and risen on low end items since retail distribution was privatized in 1993. A sales weighted price index may have indeed risen. The variety of products increased 72% after privatization. Excise tax revenues have exceeded expectations. Without more time it is not possible to determine if consumption is up due to the stocking effect of the sudden tripling in the number of outlets. Liquor retail employment rose from 1800 to 3000 within two years of privatization (Swaine, 1995).

Within a year of privatization in Iowa prices had risen about 6%. When adjusted for the rise in disposable income and the rise in the price level, the real increase was negligible. The price trend of wine and liquor was similar in other states for the same period. The privatization had no lasting impact on the overall downward trend in consumption in the state. There was also no perceived increase in cross border sales as a result of the price increase attributable to privatization (Fitzgerald and Mulford, 1993). The more recent West Virginia experience is discussed below.

The nay sayers fear a great increase in alcohol beverage consumption. The empirical debate on increased consumption attributable to privatization is ongoing and the results are mixed. both sides agree that greater off-premise outlet density has a more than proportionate effect on public drunkenness. Otherwise increasing the density of outlets seems to have little impact on consumption. For cirrhosis and per capita sales the relationship to outlet density is numerically weak, but positive. The weak relationships of income and price to the consumption of alcoholic beverages are direct and inverse, respectively. The effects of days and hours of availability are also not unequivocal. Compliance with alcohol laws seems greater in states with a monopoly regulator. In short, a privatization which does not greatly alter the number of outlets or the days and hours of operation is not likely to alter the overall consumption of alcohol in the state.

The Theory and Practice of Auctions

What Game Theory and Economics Tell Us

A seller takes a good to auction because she cannot determine ex ante the value that consumers would assign to the good. When goods are sold to all comers at a fixed price there will be a difference between the price paid and the buyers' valuation of the good. That difference is known as consumer surplus. Firms are in the business of trying to capture as much of that surplus as possible. Under a wide range of circumstances, there is no other mechanism which can capture a greater share of the consumer surplus for the seller than an auction (Wang, 1993).

To be successful at auction, the seller must be able to make a credible commitment that she will not change her procedures after seeing the bid(s). That is, if there is a bid which would have been acceptable under the announced rules of the auction, the seller cannot then renege. It is also necessary that the seller does not know the bidders' valuations. If the seller knows the bidders' valuations then she will simply announce a price to extract the highest possible value.

There are four common types of auctions used in the world today. In the open, oral English auction the price is successively raised by the auctioneer until only one bidder remains. The winning bidder pays a price which is below his own valuation of the good, but is at least equal to the value assigned by the next-to-last bidder. This auction is efficient in the sense that the good will go to the bidder who values it most highly. This type of auction is quite common in the United States and is used to sell everything from stocks, to antiques and art, to wine.

In the open, oral Dutch auction the auctioneer starts at a high price, so high that no one could conceivably agree to it. The price is then successively lowered until one bidder accepts the current price. Again, the good will be assigned to the person who values it most highly. The price paid will be below that valuation, but above the valuation of the next highest participant. This type of auction is used in Europe to sell fresh cut flowers, fish and other commodities.

In the first-price sealed-bid auction, potential buyers submit sealed bids. The highest bidder is awarded the good for the price she bid. There are scenarios under which this auction form is not efficient. Nevertheless, it is used in many venues. In the U.S. it has been used to auction everything from timber, to oil exploration rights, to alcohol beverage distribution rights.

In the second-price sealed-bid auction, bidders submit bids having been told that the highest bidder gets the item but pays only the amount of the second highest bid. Again, this auction form can produce a result in which the person with the greatest valuation does not win the auction. This auction form has been used in the sale of foreign exchange, the magnetic spectrum and mineral rights.

Within each of these four basic types of auction there are a number of variations. In some instances the seller announces a reserve price. A bid must come in above the reserve price or the good is withdrawn. Typically a reserve price is used when the good has some value in use to the seller.

To limit collusion and to keep the auction moving, bidders may be allowed only a limited time to submit their bids. The effect of collusion is to reduce the seller's ability to narrow the difference between the value of the good to the buyer and the price she must pay for the good. In the same spirit there may be a minimum increment to the highest existing bid in an English auction.

Bidders may be charged an entry fee for the right to participate in the auction. This practice is used to make sure that participants are both serious and qualified bidders. In some instances the participant forfeits her entry fee if she defaults on a winning bid.

The seller may require not only a purchase price but a royalty to measure the true value of the good or the intensity of its use. This mechanism is used in auctioning oil exploration rights. The winning bidder pays a fee for the right to explore. Once production begins the firm pays a portion of the gross revenue from the well to the government. Within this there are really three forms. Bidders may bid on the one time fee, taking the royalty as fixed. They may take the fee as fixed and bid on the royalty. Or they may construct a bid on both parts.

Of course, there is a moral hazard problem in the use of the one time fee and royalty format. The conventional use of 'moral hazard' is in the study of insurance. Selling the owner of a building a fire insurance policy provides an incentive for the owner to be less cautious in securing his building against fire. The concept is applicable in auction markets as well. For example, the seller cannot count on the oil wildcatter to exploit the successful oil well to its fullest extent since he must share the proceeds of his efforts with the seller of the good. There is a way to circumvent this. Instead of selling the good the seller might offer shares in the good. In this way the success of the winning bidder is inextricably tied to the seller.

Any of these auction forms can be used to sell goods for which more than one unit is available. In multi-unit auctions, in which the bidder makes an offer on both price and quantity, the auction may be either competitive or discriminatory. In a competitive auction each bidder gets his quantity at the price offered by the lowest bid still found acceptable to the seller. In a discriminatory auction each bidder pays his own bid price.

A Benchmark Auction Model:

In order to compare and contrast the outcomes of the four auction forms, economists have developed a benchmark auction model. The assumptions of the model are: 1. The bidders are risk neutral. That is, they would be indifferent between, say, being given $.50 in cash or receiving $1.00 when a coin toss came up heads and receiving nothing when it came up tails.

2. Bidders have independent private values. That is, each of them values the good intrinsically, but they don't know the valuations assigned by their competitors. This assumption is most applicable at an antiques auction in which the participants are not dealers, so all are anticipating buying the good for their own use, not for resale.

3. The bidders are symmetric. In the formation of their private, independent values, the bidders are not distinguishable from one another. For example, in bidding for a rare vintage of wine both bidders believe that they can resell the bottle or buy it elsewhere for $100 with probability .6 and $150 with probability .4. Before bidding they each get a draw from the probability distribution, but keep knowledge of it to themselves.


4. The payment is a function of bids alone. This eliminates consideration of entry fees, penalties and royalties. The assumption is more for reasons of simplicity, as none of these charges change the results.

Under these four assumptions each prospective buyer will bid something less than his true valuation of the good. The difference is the economic rent captured by the successful bidder. A successful bidder will have bid just enough to equal the value assigned to the good by the person with the second highest valuation, knowing that the number two person will also bid less than his true valuation by the same logic.

Whether or not we invoke any of the assumptions, the Dutch auction and the first-price sealed-bid auction will yield the same revenue outcome, on average. The intuition is that no participant reveals his valuation to the others until the good is assigned to the winner. Then it is too late to change one's bid if one had been trying to bid strategically. Hence, there is no incentive to dissemble, and everyone bids truthfully.

If all four of the assumptions are imposed then each of the four possible auctions yields the same expected revenue to the seller. This is known as the revenue equivalence theorem. However, the variance of the revenue to the seller is lower in the English and second price formats than in the Dutch and first price formats. Thus, the latter two auction forms are more risky for the seller.

It helps the seller to have more widespread participation (more bidders) in the auction. Increasing the number of bidders will increase the seller's expected revenue from the auction. The intuition is that the extra competition from more participants forces everyone to bid closer to their true valuation in order to make the likelihood of submitting a winning bid as high as possible.

An increase in the variance of the valuations will increase the average revenues to the seller. A greater variance in valuations will cause there to be a larger number of extreme bids from participants. With more extreme bids, there is a greater likelihood that the difference between the highest and lowest bid will be greater. Similarly, there is more likely to be a greater difference between the highest valuation and the second highest valuation. Hence, an increase in the variance of valuations also increases the surplus captured by the successful bidder.

In the benchmark model it is optimal for the seller to impose a reserve price, as this will cause the eventual sale price to be higher. This is a result of the fact that the winning bid cannot come from the lower tail of the distribution governing buyers' behavior. However, the reserve price may be below a participant's valuation but above his bid in the absence of a reserve price. The consequence is that the marginal bidder will raise his bid. This has a cascade effect all the way through to the bidder with the highest valuation.

Each of the assumptions of the benchmark model can be relaxed in turn. The auction outcomes are then seen to depend on the form chosen. The effects on the seller's ability to maximize the sale price of the good as each assumption is relaxed are examined in the following:

Relax Assumption 1: Risk Averse Bidders

With risk averse bidders the seller produces a larger expected revenue with a first-price sealed bid auction than with the English or second price auction. This results from bidders not seeing their competitors' strategy and wanting to avoid the risk of losing the good altogether. Participants bid more aggressively, and are willing to give up more of the surplus they would have captured in the English auction.

Insurance can play a role in auctions. The optimal auction in which bidders are risk averse involves subsidizing high bidders who lose and penalizing low-bidders who lose. This makes bidders prefer to win, eliciting higher bids, since they are being partially insured. In effect participants are being penalized for trying to low-ball the auction. This makes them bid more aggressively. That they receive a payment for their aggressive bidding serves to insure them for having lost out on ownership of the good. Since the auction is optimal, some of the high winning bid is used to subsidize the high bidding losers.

Concealing the number of bidders has the effect of making the bidding more competitive. If a participant knows that there are a large number of participants he also knows that it is very likely that the second highest valuation is close to his own, and he will bid more aggressively. If the number of bidders is unknown, then the risk averse bidder will assume the number to be large.

Relax Assumption 2: Correlated Values

That bidders' valuations are independent of one another is an extreme assumption. It is more plausible to believe that as a bidder's estimate of the value of the item rises, she expects higher values for other bidder's estimates become more likely. In a sense, the bidders establish a common value for the item. We say that the bidders' valuations are affiliated.


In the most extreme common value case the item has a true unique value, albeit unknown, about which all the bidders must make a guess. Their individual guesses differ; for example, they differ in their ability to use the good in production or to resell the good. In the model with common, or affiliated, values the winner is the one with the highest guesstimate of the good's value.

The assignment of the good to the bidder who guessed its value to be greatest is known as the winner's curse. Bridge players know that failure to make a bid is most common after hotly contested bidding. This is an example of the winner's curse in that the successful bidder has overvalued his hand in the process of winning the bid. In bidding for a good or bidding for a supply contract, the true value of the good is more accurately reflected in the average bid rather than in the bid of the eventual winner. While seeming logical, this defies rationality in repeat situations since it assumes that bidders never learn.

The rational bidder in a sealed bid auction avoids the winner's curse by bidding what he believes to be the second highest valuation. That is, he bids more cautiously. Hence, the seller trying to maximize the sale price of the item should eschew silent auctions.

When bidders' valuations are affiliated, the seller's expected revenue can be ranked in descending order by auction form from the: English auction, second price sealed bid, first price sealed bid, and the Dutch auction.

The seller can exploit the affiliated valuations of the competitors and increase his expected revenue by publicizing information he may have about the true value of the item. Being aware of the winner's curse problem, competitors will tend to revise downward their own valuation and bid more conservatively. If the seller can reveal information about the item's value to all participants, then they will all become less cautious.

For the same reason that the seller should reveal information, she should set the reserve price in a common value above her valuation. The reserve price serves to drive up the mean valuation of the item.

On the other hand a bidder should lower her bid to compensate for her past inclination to overestimate in auctions she won. She should also lower her bid to include a profit margin. She shouldn't let the presence of more competing bidders push her into bidding too aggressively.

Empirical work (Hendricks and Porter, 1993) confirms the theoretical conclusions where there are information asymmetries and affiliated values. In addition, the less informed participants are seen to be less likely to participate and the winning bids tend to be lower. These same studies have shown that the structural bidding strategies in private and affiliated values models can be recovered (estimated) statistically. Potentially one can use cross sectional experience to model bid behavior in an ex ante situation.

Relax Assumption 3: Asymmetric Bidders

When bidders are asymmetric their bids are made as though they are drawing from different distributions. In the earlier example the two participants drew their valuation from the same distribution and for each of them the average value was the same. In the asymmetric case the bid distribution means need not be the same. The auctioneer still awards the good to the highest bidder, but the highest bidder need not have the highest valuation. This is due to the fact that in part the size of the difference between the valuation and the bid depends on the sizes of the heterogenous classes of bidders. A simple example illustrates the case. Mr. A values the object at $65, and he will always bid a little less than this, say $64. Mr. B thinks he can find a buyer for the object at $50 with probability ½ and a buyer for $75 with probability ½. So the item is worth $62.50 to Mr. B, and he bids a little less, say $61. The auction takes place and Mr. A will always win. But later a $75 buyer for the item may approach Mr. B, hence B's final value is indeed greater than A's, who won the auction.

As in the previous example, suppose there are two classes of buyers. Their valuation distributions are identical except for the mean. On average those in class 1 assign the higher value to the item. Then the optimal auction favors the class of bidders with the lower mean value. That is, the participants in class 1 reduce their bids systematically, thinking that they need not bid so aggressively in order to beat those in the other class. Those in class 2 will increase their bids systematically, thinking that they need to be more aggressive in order to beat the higher valuations in class 1. The result may be that someone from class 2 who draws his bid from the upper tail of the distribution will beat the class 1 participants who are drawing from their lower tail.

With asymmetric bidders, the English and first price sealed bid auctions will yield different revenues to the seller when bidders are asymmetric. In general it is not possible to state which will be greater and so no recommendation for the seller's optimal auction form exists. When bidders are asymmetric it is possible under the Dutch and first price sealed bid auctions for the equilibrium (outcome) not to be efficient. That is, the winner need not have the highest valuation. The English auction is always efficient.

Empirical work confirms the asymmetric bidders hypothesis that informed bidders will have positive expected profits. The difference is the value of the informed firm's private information. The participation of uninformed firms has the function of keeping the informed firms from getting the good too cheaply.

Relax Assumption 4: Royalties and Incentive Payments

In auctioning oil rights, the government does not know ex ante the bidders' valuations. After the auction the government can observe how much oil is extracted and thus the true value of the tract to the buyer. The price paid by the buyer is the sum of the bid and the royalty rate on the ex post true value of the good. The auctioneer can fix either the bid or the royalty rate or both.

If the ex post valuation of the good is exogenous then the seller's revenue is an increasing function of the royalty rate. A positive royalty lessens the differences in valuations, resulting in a lower variance of valuations and higher revenue for the seller.

If the post auction valuation depends on the effort of the successful bidder then there may be a moral hazard problem. That is, a high royalty rate will discourage the successful bidder from exploiting the use of the item for profit. Hence the optimal royalty is always less than 100%. The royalty rate is zero if and only if there is an infinite number of bidders; when there is a large number of buyers, there is more likely to be a buyer who will combine a higher purchase price and lower royalty in order to win the contract and relieve the seller of the moral hazard problem.

When buyers are more risk averse, they will offer a higher royalty rate. This has the effect of lowering the one time bid and shifting the risk of ex post value to the seller. This can be seen in off-shore exploration oil tract bidding, where the purchase fee is almost trivial, but the royalty rate (if the well comes in) is quite high.

Multi-unit Auctions:

In essence multi-unit auctions do not differ from single unit auctions. There are however, some very specialized results (Branco, 1996 and Tenorio, 1993). In the competitive format, in which the winners all pay a price equal to the lowest acceptable bid, there is likely to be higher effective bidder participation, hence revenues can be higher. At the same time, the competitive format also increases the variance of bids, making the auction more risky for the seller.

In a two competitor auction, if the sum of bidders' valuations from giving all of the units to one and none to the other is larger than that from any split, then it is optimal for the seller to bundle all of the units and organize a single auction for the entire lot. This does not seem to be generalizable to the auction with many participants (Dana and Spier, 1994).

In multi-unit auctions the seller may want to use endogenous minimum bid announcements. The minimum bid rule, or reserve price, will be contingent on the bidders' valuations. The twist is that the seller cannot announce the reserve price before the competitors' valuations are reported. In this format a winning high bidder may be confronted with a higher reserve price than a winning low bidder.

Where each of the many winning bidders gets only one unit then the optimal auctions are sealed bid uniform price and the discriminatory auction. In a simultaneous open auction the seller cannot determine the bidders' private values so this is not an optimal auction. However, where bidders may take more than one unit the optimality conditions are not clear. There are more alternative strategies and special results, but the ones described here illustrate most alternatives for privatization auctions.

Debacles and Successes in Auctions of Publicly Owned Assets

With all of these very precise predictions from the theory one can only wonder whether they are borne out in the real world and whether auction design matters. We begin with a brief review of some notable mistakes in auction design and then review the recent sales of the radio magnetic spectrum by the Federal Communications Commission.

In 1990 New Zealand chose the auction method to sell part of their spectrum for use by TV and cellular telephone. The spectrum auction was forecast to raise NZ$240 million. On the recommendation of an American consulting firm, they used a sealed bid second price auction and raised only NZ$36 million. In some markets the spectrum was essentially given away. Needless to say, the political fallout was terrible. The reason was the small number of bidders and lack of a reserve price in a second price auction. If there is only one bidder in a second price auction with no reserve price then that bidder will get the item for no charge. The same essential outcome occurs when there is no serious second bidder. The number of instances in which this happened in New Zealand was not trivial. At the very least the New Zealand government should have required a participation fee, used an English auction and set reserve prices.

In 1993 Australia's satellite TV services auction, two unknown firms submitted extraordinarily high bids in first price sealed bid auctions. These same firms also submitted a number of much lower cascading bids. When the firms defaulted on their high bids the licenses had to be awarded to the next highest bids, which belonged to these same firms. They defaulted sequentially until they got the price down to what they really were willing to pay, less than half of their original bids. The problem was the lack of a penalty for default on a winning bid.

With the examples of Australia and New Zealand behind them, the Federal Communications Commission was more cautious in its auction design when it was charged by Congress with the sale of the radio magnetic spectrum in the U.S. In fact, the auction was designed in collaboration among the FCC staff, their consultants, likely competitors and their consultants.

The wavelengths offered were those for personal communication services: pocket telephones, portable fax machines and wireless computer networks. The Office of Management and Budget valued this block at $10.2 billion. The reaction of the communications industry was gales of laughter. This high estimate came in spite of the fact that the eventual size of the market is unknown, pocket telephones in these bands will compete with existing cellular networks, much of the technology for using this bandwidth is not yet developed, and much investment will be needed to build the requisite infrastructure.

Prior to Congress' charge, the FCC had relied on administrative decision to assign bandwidth. In more recent years the band width had been given away by lottery in order to hasten the process. Lottery winners sometimes sold their licenses for a big windfall. Needless to say, there was political pressure to capture the windfall for the Treasury.

The FCC divided the country geographically and divided the spectrum by wavelength to create 2500 licenses. A stated goal of dividing the spectrum in this fashion and offering the rights of use at auction was to allow aggregation of licenses for economic and technological reasons. Efficiency was a concern since, within a region, licenses would have substitutes. That is, a different bandwidth but in the same geographic region could serve an equivalent function. There might also be complementarities in infrastructure and expertise between geographic regions. Beyond economic and technological considerations, the auction should also be designed to prevent monopolization, foster minority owned business, promote small business and finally to assign licenses to those who value them the most.

When it came time to design its auction mechanism, the FCC settled on an open, simultaneous auction of all licenses in order to reduce the force of the winner's curse and to induce participants to bid less cautiously than they would in a sealed bid auction. This decision was made in spite of the fact that a sealed bid auction will deter collusion more easily and will raise more revenue when the buyers are risk averse.

It was also decided to use multiple rounds of sealed bids, announcing all bids (including bidder identities) after each round, with a minimum increment between rounds. The multiple rounds with revealed identities and bids would allow firms to appraise their own and competitors' bidding strategies and to estimate the likely cost of obtaining the particular licenses and aggregations they wanted. In this way the firms would be able to construct alternative aggregations and strategies. The multiple rounds would also offset the winner's curse phenomenon.

Simultaneously auctioning all of the licenses at each round permitted more efficient aggregation as firms acquire information about how others value blocks they want. The rules left bidding open on all licenses until bidding stopped on all licenses. An activity rule was used to insure the auction closed in a reasonable time. A deposit was required to limit the auction to serious bidders. A bid withdrawal penalty equal to the difference between the withdrawn bid and the bid of the eventual winner was to be imposed.

The FCC favored designated classes of bidders with set asides, price preferences, and installment payments. This was meant to advance the goal of minority ownership. In the end it was decided to use discounts to favor certain classes of bidders. By giving designated bidders a discount (25%), it has the effect of driving up the bidding. A non designated firm, when there are no discounts, will bid conservatively knowing that the minority firms cannot compete.

Royalties on the use of the license were rejected as too difficult to enforce for accounting reasons. Also, given that successful bidders would have to make considerable investments in new technologies, it was decided that the moral hazard effect would be too problematic if royalties were implemented. It was decided that reserve prices would be used only for licenses where the number of bidders would be small.

As equilibrium came near, the winning bids were established on the high value licenses first. After three bandwidth auctions the FCC has raised about $8.8 billion of the projected $10.2 billion. The skeptics have been proved wrong.

Liquor License Auctions

In order to estimate the revenues generated in a well designed auction of liquor licenses in Pennsylvania, one need look no further than a neighbor to the southwest, West Virginia. On February 27, 1990 Senate Bill No. 337 was passed by the State of West Virginia Legislature. The bill was enacted to permit the retail sale of distilled spirits by licensees of the state. This would complete the process begun with the sale of beer and wine through licensed, privately owned outlets.

The Liquor Licensing Board divided the state into 98 market zones. The Board then proceeded to allocate 124 single and multiple site franchises among the zones. About 82% of the franchises would be exclusive, conferring on the winning bidders a local monopoly. With the full implementation of privatization there could be as many as 214 retail outlets, an increase from 156 in the last year of the state monopoly.

The bid processes took place in August 1990, January 1991 and May 1991. Auction winners paid $15,222,615 for the right to open retail outlets in the state and remain in operation until their permits expire in June 2000. The winners then had to pay their annual franchise fee and make any necessary investment in plant and equipment and merchandise inventory before opening their doors for business. Operating expenses such as rent and wages would be in addition to whatever was paid for the license.

Extensive supporting documents were prepared for potential bidders. The documents included criteria for eligibility and rules for submitting bids. Competitors had to file a form with the bureau of investigation for a brief background check. Two functions were served by this. First, it discouraged those with a criminal record from trying to participate. Second, it allowed the state to verify the residence of participants. While the auction was open to both residents and non-residents, the former were given a 5% advantage in the bidding. That is, a non-resident had to beat a resident by 5% in order to win the license. From the theory we know that this has the effect of making non-residents bid more aggressively.

With each sealed bid the competitors had to submit a bond valued at 25% of the highest price offered for a license in their bid applications. In the event that a winning bidder could not make payment, the bond would be forfeited to the state. This keeps those who are not serious from participating in the process, and it precludes the cascading of bids as in the Australian example.

A bid could include offers on any number of licenses, or an aggregation of licenses. In order to win an aggregation the offer price had to beat the sum of the highest individual bids submitted by others on each of the licenses involved. To the extent there are any economies of large scale in retailing, allowing competitors to aggregate their choice of licenses will foster efficiency.

The documents indicated that the state would not award a license for which there were no acceptable bids. Furthermore, if winning bidders did not open for business within a reasonable time, or if a license was unsold, then the state reserved the right to continue doing business in the affected zones. In the parlance of the previous section this was equivalent to a random, unannounced reserve price. The theoretical results indicate that a reserve price has the effect of making bidders more aggressive. The results on announced versus unannounced reserve prices are not clear. In the West Virginia case the lack of announced reserve prices probably contributed to the need to go to three auctions.

In addition, detailed socioeconomic data were provided about the counties in which the market zones were located. The data were all from the public domain and could be found in, for example, the County and City Data Book, a well known source of marketing information. From the population, employment, income and retail sales data the potential bidder could make an informed judgment about the demand for alcohol beverages.

The state also furnished sales and cost information about the existing state stores in each market zone. There was a rough correspondence between the existing state liquor stores and available licenses. Some of the stores were quite profitable. Other stores, largely due to low volume, had been unprofitable in the years leading up to the auction. The competitors could use the cost and sales data to assess the likely rate of return on their investment in a license.

The West Virginia auction had elements of both independent private values and affiliated values. The theoretical results show that, in an affiliated values auction, the effect of making information widely known is to increase the expected yield to the seller. The ex post evidence is that the bidders made little use of the economic information beyond liquor sales and total retail sales in the zone of interest.

The original intent of the Liquor License Board had been to sell all of the stores in one round of bidding. Instead, some of the properties were withheld for reason of unacceptable bids. The result was to cause the bidding process to mix aspects of sequential and simultaneous auctions of multiple homogeneous goods. There is no theory with which to model the likely resulting behavior. Two observations are worthwhile nonetheless. (See Table 1.) First, the more valuable franchises tended to be sold in the first round in August 1990, although there were a few exceptions. On the other hand, adjusting for the number of outlets permitted per license shows that competitors valued the return on investment potential about equally in the two rounds. The least desirable franchises were clearly sold in the last round. Second, bidders participating subsequent to the first round could infer the state's reserve prices from decisions in the early rounds. While the more transparent reserve prices would make bidders more aggressive, the sequential nature of the auction may have discouraged further participation both by winners in the first round and by those who had come away empty handed. Recall that the FCC kept bidding open on all licenses in its simultaneous auction until a price had been reached on every license. This had the effect of allowing competitors to switch from a license which was financially out of reach to licenses which were still priced fairly low.

Table 1
Results of Multiple Rounds

Date

Total Revenue

Licenses

$ per Outlet

August 1991

$7,639,359

59

$63,916

January 1991

$6,539,146

51

$64,910

May 1991

$1,044,210

14

$47,677

In reviewing the winning bids it becomes apparent that there were bidders with different kinds of financial backing. (See Table 2.) The Southland Corporation (7-11) of Dallas and Rite-Aid of West Virginia were the largest corporate winners. Both bid on and won numerous licenses, though their bidding behavior differed. Several regional retailers, for example Big Bear and Giant Eagle, also bid on and won numerous licenses. Finally, many local residents won licenses. The bidding power of the four groups differed markedly.

Table 2
Bidding Behavior of Identifiable Groups

Competitor

Average Bid

Licenses

Southland

$187,328

9

Rite-Aid

$112,432

33

Regional

$285,062

17

Local

$76,622

65

Of the corporate bidders, Rite-Aid was clearly the most conservative. It is somewhat surprising to see how conservative Southland was relative to the regional bidders. The regional group was dominated by grocery chains seeking to leverage their existing infrastructure into one-stop shopping for their customers. The locals may have been capital constrained in their bidding, although economic theory suggests they should have been able to borrow in order to compete for the more lucrative franchises.

A license restricts the number of outlets a winning bidder may have in a market zone. There are no restrictions on the location of the outlet(s) in the zone. A license holder may also apply for permits to distribute wine and beer. In fact, this has not been common. A retail license holder may also obtain state and federal approval for wholesale distribution to the restaurant trade. There are a number of cases in which the license holder has failed to file for the wholesale permit, to the chagrin of restaurateurs.
In the year 2000, when the licenses expire, a new auction will be held. In recent testimony before the West Virginia joint legislative committee responsible for oversight of liquor distribution, current license owners have lobbied for a version of a 'right of first refusal' rather than have to reenter the auction process.


In order to infer the likely success of auctioning franchise rights to liquor and wine distribution in Pennsylvania, a regression model of the West Virginia experience was constructed. A generic regression model of the auction is

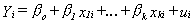
in which i represents the observation on the ith bidder, Y_i is the winning bid, the x_ji are a set of variables used to explain the winning bid, u_i is an error term to capture unobservables in the auction process, and the b_j are a set of unknown parameters to be estimated. In this exercise the parameters have been estimated by ordinary least squares (OLS).

The most important results of the exercise are reported in Table 3. As noted above, the West Virginia Liquor License Board provided interested buyers with a book which included socioeconomic data as well as data about the existing state liquor stores. Any of these socio-economic measures would be legitimate candidates for the right hand side of the regression model. Surprisingly, bidders seemed to use only a small part of this data.

In addition to the store financial data for a given market zone, the bidders also had available the sales data for adjacent market zones, the number of outlets that could be opened in a market zone under privatization, and data on product mix and prices. The economics of liquor retailing are such that bidders could use either gross sales, sales net of state taxes, or operating profit in valuing a franchise. They do not appear to have used any of the product price and mix data in forming their bids.

The economic data included the number of retail establishments in each county and corresponding sales, population, square miles, number of households, unemployment and per capita income. The only data which seem to have entered bidders' valuations were retail sales per household.

Because of the character of West Virginia and the behavior of the identifiable groups of bidders, it was necessary to include dummy variables for urban areas, areas in which alcohol beverages cannot be sold, and for competitors whose bidding strategy differed from the rest of the field of competitors.

Econometric modeling is as much an art as a science, involving the judicious inclusion and exclusion of exogenous variables on the right hand side of the equation. The last row of table 3 reports the coefficient of determination, or R², for the equation. In this case the R² shows the proportion of the variation in bid prices which can be explained by the included exogenous variables. The R² can be as low as zero and as high as one. The simplest model with dummy variables for class of bidder and whether market zone is 'dry', as well as variables for retail sales per household and the number of outlet licenses in the bid, the proportion of variation explained is 54%.

The two rows preceding the coefficient of determination report a test statistic for the homoscedasticity of the error term (LM for hetero) and a statistic (Condition Number) for the extent to which the right hand side variables show co-movement (Greene (1997) at pps. 550 and 422, respectively). In every case it can be concluded that he error term in the model is not homoscedastic. The consequence is that while the OLS estimates of the unknown parameters are unbiased, they are not efficient.

A condition number above 20 is usually regarded as indicative of multicollinearity, or co-movement of the right hand side variables. The second, sixth and seventh models show multicollinearity. The consequence for estimation is that OLS estimators are unbiased, but not measured very precisely.

In the second column the model was expanded to account for the fact that some jurisdictions would allow competition among license holders. The second model also includes liquor sales per existing 'state store' in the market zone. The effect of allowing competition is to reduce the amount of the winning bid; the sign on the estimated coefficient is negative. For every additional dollar of liquor sales by an existing state store in the zone, the winning bid rose by $.27.

In succeeding columns additional variables were added in order to capture the potential richness and complexity of the license valuation process made possible by the data provided to participants. Regardless of the specification of the model, certain patterns emerge. All other things equal, the Southland Corporation paid a substantial premium, beyond that paid by either Rite-Aide or the regional retailers. The licenses sold in round 1 were deemed far more valuable than those sold in subsequent rounds. The round 1 premium was only about half that paid for franchises in urban areas. In the last two columns it is apparent that unemployment and household income did not matter much in forming the winning bid, in the sense of statistical significance.

For purposes of assessing bidding behavior, the best model in Table 3 is in column five. This model has one of the highest R², the condition number is moderate, the LM statistic is not too much out of line with the other models, and the signs on the individual coefficients are what one would expect. Southland and the regional grocery chains paid a premium for licenses. Licenses which were sold in the first round or were in an urban area went at a premium. Dry areas and the presence of competitors in the zone both reduced the bid price. Higher general retail sales, more outlets per market zone, and previous liquor sales all elicited higher bids for a given license.

On the basis of these results one can say that, all other things equal, Southland can be expected to pay $88,645 more for a license than other bidders. A regional chain paid $16,596 more. Participants bid so much more aggressively on the more valuable properties that those franchises sold in the first round accrued higher bids by $24,998. Competitors bid $55,131 more for a license in an urban market than for a license in a rural market, all other things equal. If a market zone was wholly dry, then the valuation of the license was reduced by $65,627. Because some of the franchise licenses permitted multiple outlets, a variable indicating the potential number of stores available to the winner was included. Each additional outlet associated with a winning bid served to raise the winning price by $129,756. By the same token, not all franchises conferred a local monopoly on the winner. For each additional competitor allowed into a market zone, the value of the license fell by $16,786. For every additional dollar of retail sales per household in the county in which the franchise was located the winning bid price rose by $7.10. Finally, for every dollar increase in sales net of taxes, competitors raised their bids by $.25.

To illustrate how one could use these results for Pennsylvania, consider the franchise rights for the four Liquor Control Board stores in Cheltenham Township in Eastern Montgomery County. This is an urban area in the sense applied in the West Virginia study. Suppose in one scenario that a bidder is allowed to buy a single franchise permitting four outlets; there are no competitors permitted in the zone. The winning bidder, we can safely assume, will be a chain grocery operator of magnitude similar to Southland Corporation. Since Cheltenham is a valuable location, we be sure it would sell in the first round of any auction. Retail sales in Cheltenham last year were about $34,000 per household, and combined gross sales by the four stores were $6,962,742. Plugging all of this information into the regression model yields a forecasted winning bid of $2.2 million dollars. This may, in fact, underestimate the true value at auction since the West Virginia residents were bidding on a system which had previously privatized its wine distribution, while Pennsylvania has only privatized beer sales. On the other hand, wine sales are included in the Pennsylvania sales figure.

Using the regression results it is possible to give some ball park figures for the auction value of the wine and liquor franchise rights in Pennsylvania. Cheltenham accounts for about .8% of the combined wine and liquor sales in the state. Extrapolating from the winning bid in the last paragraph one might expect to realize about $270 million for the franchise rights in the entire state. Even if one used only the regression coefficient for the liquor sales variable, one could expect the state to receive $170 million in franchise rights. The sale of merchandise inventory and physical plant would add more to these estimates. And one should be mindful that, as the monopoly wholesaler the state's alcohol beverage tax base is bounded only by the work ethic of the new retailers, the tax rate and retail demand.

 Table 3:  Bidding for West Virginia Liquor Licenses

Eqn

1

2

3

4

5

6

7

Constant

-306255
(-6.78)

-264250
(-6.05)

-231154
(-4.66)

-264228
(-5.61)

-258377
(-5.50)

-216303
(-3.07)

-151366
(-1.84)

South-land

121884
(2.68)

101802
(2.36)

85564
(1.91)

90704
(2.02)

88645
(1.99)

81862
(1.73)

97453
(2.13)

Rite-
Aide

13716
(.54)

Region

68525
(1.91)

29915
(.83)

16596
(.45)

Local

-22251
(-.95)

Round 1

26488
(1.18)

24998
(1.10)

27605
(1.24)

27618
(1.25)

Urban

51439
(1.20)

58462
(1.36)

55131
(1.27)

57025
(1.34)

60457
(1.43)

Dry

-73073
(-1.85)

-64534
(-1.70)

-64236
(-1.71)

-70255
(-1.86)

-65627
(-1.72)

-69960
(-1.87)

-75480
(-2.02)

Outlets

136308
(8.67)

127616
(8.34)

127234
(8.35)

130741
(8.78)

129756
(8.47)

136951
(9.22)

136371
(9.22)

Comp

-10112
(-1.15)

-18100
(-1.79)

-18845
(-1.86)

-16786
(-1.58)

-37436
(-2.75)

-33974
(-2.46)

Retail

13.45
(5.21)

7.65
(2.61)

7.51
(2.58)

7.31
(2.50)

7.10
(2.41)

7.15
(2.43)

9.07
(2.65)

Liquor Sales

.27
(3.97)

.26
(3.85)

.26
(3.89)

.25
(3.59)

.16
(1.91)

.16
(2.01)

Income

-9.07
(-1.02)

Profit

.27
(2.09)

Unemploy-
ment

-148
(-.03)

LM for Hetero

355.7

428.6

350.6

364.1

417.8

308.9

306.6

Condition
Number

9.01

67.21

13.63

13.44

13.43

20.41

31.75

R2

.54

.60

.61

.61

.61

.63

.63

Conclusions

In light of economic theory and the experience of West Virginia and the FCC, it is possible to make some recommendations for the design of an auction of wine and spirits retail distribution licenses in Pennsylvania.

1. Reserve prices on the franchises should be announced ex ante.

2. All relevant economic data should be made available to all competitors prior to the auction.

3. All accounting data for each existing store should be made available to each competitor.

4. Franchise rights should be geographically exclusive, though not necessarily correspond to existing stores.

5. Competitors should be required to post a bond to be forfeited in the event that they are not able to make payment on their winning bid.

6. The licenses should be auctioned in a simultaneous, multi-round auction. All licenses are to be in play until a high bid is reached on all licenses.

7. The amount and identity of the high bid on each license should be announced at the end of each round.

8. In order to remain in the bidding each competitor must post a minimum increment bid on at least 25% of the licenses in which she had previously expressed interest.

Barring cataclysm, and assuming underlying similarities with West Virginia, such an auction could raise in excess of $200 million in ten year franchise rights, on top of the annual tax (and profit) revenue already collected by the Commonwealth.

Bibliography

Branco, Fernando, 1996, "Multiple Unit Auctions of an Indivisible Good", Economic Theory, Vol. 8, Pps. 77-101.

Buck, Andrew J. and Simon Hakim, 1991, Privatizing Liquor Sales in Pennsylvania, The Commonwealth Foundation for Public Policy Alternatives, Harrisburg, PA, June.

Dana, James D. and Kathryn E. Spier, 1994, "Designing a Private Industry: Government Auctions with Endogenous Market Structure", Journal of Public Economics, Vol. 53, No. 1, Pps. 127-147.

Fitzgerald, J.L. and H.A. Mulford, 1993, "Privatization, Price and Cross-Border Liquor Purchases", Journal of Studies on Alcohol, Vol. 54, No. 4, July, Pps. 462-464.

Greene, William H., 1997, Econometric Analysis, third edition, Prentice-Hall, New Jersey.

Hendricks, Kenneth and Robert Porter, 1993, "Bidding Behavior in OCS Drainage Auctions: Theory and Evidence", European Economic Review, Vol. 37, Pps. 320-326.

Holder, Harold, 1993, "The State Monopoly as a Public Policy Approach to Consumption and Alcohol Problems: A Review of Research Evidence", Contemporary Drug Problems, Vol. 20, No. 2, Summer, Pps. 293-322.

Laffont, Jean-Jacques and Quang Vuong, 1993, "Structural Econometric Analysis of Descending Auctions", European Economic Review, Vol. 37, Pps. 329-341.

McAFee, R. Preston and John McMillan, 1987, "Auctions and Bidding," Journal of Economic Literature, Vol. 25, No. 2, June, pps. 699-738.

McAfee, R. Preston and John McMillan, 1996, "Analyzing the Airwaves Auction", Journal of Economic Perspectives, Vol. 10, No. 1, Winter, Pps. 159-176.

McMillan, John, 1994, "Selling Spectrum Rights", Journal of Economic Perspectives, Vol. 8, No. 3, Summer, Pps. 145-162.

Milgrom, Paul, 1989, "Auctions and Bidding: A Primer", Journal of Economic Perspectives, Vol. 3, No. 2, Summer, Pps. 3-22.

Riley, John G., 1989, "Expected Revenue from Open and Sealed Bid Auctions", Journal of Economic Perspectives, Vol. 3, No.2, Summer, Pps. 41-50.

Swaine, Margaret, 1995, "The Case for Privatization", An Information Symposium on Alcohol Privatization/Deregulation, Nov. 20, Toronto, Canada.



Tenorio, Rafael, 1993, "Revenue Equivalence and Bidding Behavior in a Multi-unit Auction Market: An Empirical Analysis", Review of Economics and Statistics, Vol. 75, No. 2, May, Pps. 302-314.

Wang, Ruqu, 1993, "Auctions versus Posted Price Selling", American Economic Review, Vol. 83, No. 4, September, Pps. 838-851.