Consumer Discrimination in Baseball

by

Derek Oh and Andrew J. Buck

JEL Classification: J7, L83

ABSTRACT

Consumer Discrimination in Baseball

by

Derek Oh and Andrew J. Buck

In this paper we construct a simple model of discrimination to demonstrate that observationally one cannot distinguish between the different sources of apparent salary discrimination in sports. We also show that, contrary to a popular belief, observed racial differences in baseball trading card prices may be a result of forces other than consumer discrimination. Using actual trading card prices, we find no evidence of pricing differences by race.

Consumer Discrimination in Baseball

by

Derek Oh and Andrew J. Buck

There are three sources of discrimination which may drive a wedge between productivity and wages (Becker, 1971). Employer discrimination may be a result of nonconvexities in the cost of adjusting the firm's labor for ce (Arrow, 1972) or may be the result of the firm's inability to screen/sort employees (Spence, 1973). The employer may discriminate in response to discrimination among coworkers (Lindsay and Maloney, 1988). Finally, discrimination in employment may be th e firm's response to consumer tastes.

Professional sports labor markets provide a unique opportunity to explore the different sources of discrimination.

An overview and survey can be found in Kahn (1991). This paper uses the market for baseball player trading cards to determine the presence of discrimination by consumers. Nardenelli and Simon (1990), Andersen and LaCroix (1991) and Gabriel, Johnson and Stanton (1995) used this approach and concluded that consumer discrimination exists in the market for baseball cards.

The present paper differs from earlier work. First, we construct a model in which observations on wages and employment cannot identify the source of discrimination. Second, we reconsider the assertion that the market for baseball cards abstracts from e mployer discrimination. Third, the sample year has been changed in order to avoid certain problems which may have predisposed earlier efforts toward finding discrimination. Finally, model specification seems to play a critical role in concluding that disc rimination exists in the baseball card market.

The order of the paper is as follows. In section 2 we provide an overview of research on discrimination in professional sports. In section 3 we offer a critical reexamination of consumer discrimination in baseball. The paper closes with conclusions and suggestions for further research.

Previous studies show the presence of a wage gap between whites and blacks in basketball (Kahn and Sherer, 1988, and Hamilton, 1997) and baseball (Hill and Spellman, 1984 and Scully, 1974). The literature is surveyed by Kahn (1991). The persistence of these gaps begs the question of the source. While the focus of the paper is consumer discrimination, some comments on other sources are in order, and are best couched in terms of a formal model.

If the owner were only interested in the bottom line, then s/he would simply maximize subject to the production constraint, and employer discrimination would not exist. Even if every other owner in the league d id not discriminate there would still be a place for the prejudiced owner since there is a minimal number of teams necessary for playoffs. That is, there have to be at least three teams for there to be an end of season tournament to decide on the 'world c hampion'. Furthermore, as long as the team breaks even, the owner can indulge in her taste for discrimination. At least superficial evidence suggests that the standard inference about the marketplace eliminating employer discrimination is dubious. First, some baseball teams did not become integrated until long after Jackie Robinson broke the color barrier in 1947. The Phillies and the Red Sox held out until 1957. Second, some owners, like Marge Schott of the Cincinnati Reds, are quite open about their tas tes for discrimination. Finally, if market forces were sufficient to eliminate employer discrimination, then one would expect the racial composition of different teams to be approximately equal. With this in mind, the utility function of the ow ner behaves as

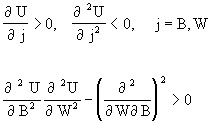
But if the owner prefers players of type B to those of type W, an equality would hold if the owner had no racial preferences, ceteris paribus. This is much weaker than the standard assum ption that the marginal utility of employing a black player is negative.

Another characteristic of the model is that. This permits players to express their tastes for their teammates' type by demanding a higher wage to play with a less homogeneous team. There is empirical eviden ce that suggests that the salary differences of white and black players cannot be explained by performance alone and players have been known to move from one team to another just so that they can play with particular persons.

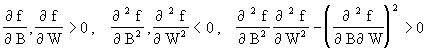
Whites and blacks are of equal ability, but they are more productive when playing with other members of the same racial group. As the team becomes more B-like, the marginal product of type B players rises. That is . On the other hand, as the degree of B-ness rises, the marginal product of type W players falls. That is . In either case, more homogeneous teams will have better won-loss records.

There is evidence that teamwork, the ability to produce output for consumption by the public, is affected by race. The small number of black quarterbacks in the NFL and their infrequent trips to the Super Bowl is suggestive. The quarterback is generall y viewed as the leader and guiding force on the team. The opportunity to play the position depends on a management decision, but one's longevity in the position depends greatly on the cooperation of the rest of the team. Regardless of one's skill, the tea m can frustrate the quarterback.

It has been asserted that in the long run, mobility and self-sorting by workers will cause coworker discrimination to disappear. This is not a result of the above specification. Nor is it born out by consideration of the institutions of professional sp ort. The mobility of players is a fiction in most professional sports which is only now beginning to change. Self-sorting relies not only on player mobility but the team owner's total devotion to profit maximization. This seems a dubious assertion as well . The record of the Sixers in the NBA in the 1990s suggests that there are motives other than profit maximization at work.

Finally, the demand curve is a function of the racial composition of the team in order to permit discrimination by consumers. We assume, but to reflect consumers' discr iminatory tastes. Such discriminatory tastes can persist since consumers have many choices in the market place; if the hometown team doesn't cater to the audience's preferences, then the fans can always choose a different sport or tune their TV or radio t o another city.

The usual maximization calculus gives the following first order conditions

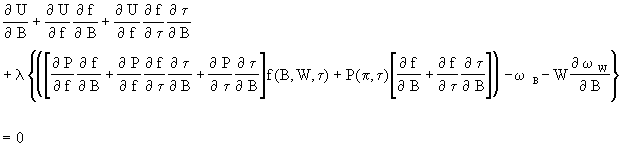
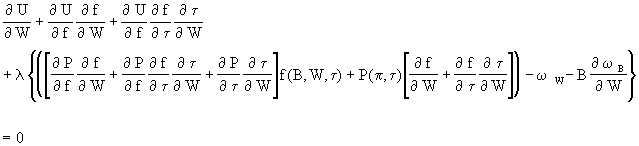
The first order conditions could be solved for the equilibrium services of B and W players. Suffice it to say, observed employment will not depend on the marginal products of the players and wages alone. Rather, they will depen d on all of the possible sources of discriminatory behavior. The first order conditions show that even if the employer does not discriminate, a wage differential may arise from either coworker discrimination or consumer discrimination. If employment is to be based solely on the equality of the ratio of marginal product and wages, then all sources of discrimination must be eliminated. The empirical implication is that even if one could measure the marginal products of the players, say with performance stat istics, the equations defining the demand for players still would not permit identification of the source of an observed wage differential.

A derivative market exists which can be used to determine whether consumers discriminate against athletes of different types. It is purported that baseball cards allow the researcher to separate a player's entertainm ent value and his ability to do the job. The first of these papers, Nardinelli and Simon (1990), found discrimination by consumers against black and latino hitters and pitchers. Using different sample years and specifications, Andersen and LaCroix (1991), reported mixed results. Their most interesting conclusion was that black players' cards increase in price with an increase in performance less than the increase for whites, for both hitters and pitchers. Gabriel, Johnson and Stanton (1995) examined the c ard prices of rookies. They do not find that card prices are influenced by ethnicity.

The institutional features of the card market aside (we offer these details later in the paper), the value of a player's card should be determined by the player's career performance and the scarcity of the card. In an ideal world, performance and avail ability should account for the price difference between a white player's card price and a black player's card price. There should be no room for either employer or coworker discrimination to affect card prices. But the world is far from perfect.

Again, a simple model illustrates the essential points. Similar to actual practice, we assume that the number of cards distributed by a publisher is determined at the start of the season. Regardless of how the season develops, the publisher does not pr int any more cards for a given player until the next year. Hence, the supply curve for trading cards for a given player is perfectly inelastic and is given by Q_s.

The demand for a player's card, Q_d, depends on his lifetime performance statistics, his observed ability (a), and the price of his card (p). The price of other players' cards (p_s) will also affect the price for a given card due to the fact that cards are collected as sets. An individual's card and other cards are complements. Hence, we assume the following:

Consumer tastes will also affect demand (t). The price of a player's trading card may reflect consumer preferences at the time the player was active. Consumers may not want to see a particular player and so choose to not attend his games. In response to the market, the owner doesn't field that player. The player's performance lifetime statistics will then be low and the price of his trading card will not reflect his true ability. Another possibility is that a player's gloss may be tarnished by behavior after his career has ended. The prices of some players cards have changed sharply long after their life time statistics were already known.

The model is,

Q_s =

Q_d - = 0

A simple application of the implicit function theorem provides a demonstration that "... the link between consumer racial attitudes and the price of baseball cards is direct. There is no room for owner or coworker discrimination." is an overstatement. Specifically,

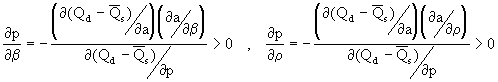
An owner disposed to putting an individual on the field will have a positive effect that player's card price and if there is a spirit of teamwork among the players then that individual's card price will be higher, ceteris parib us.

Our caveats aside, baseball cards seem to be the best game in town for measuring consumer discrimination, but some care must be exercised. There are certain institutional features of the card market which make the ch oice of sample year an issue. The sample year must be chosen so that differences in card prices can be attributable solely to consumer tastes.

Baseball cards have been a feature on the American sports scene since the 1890's, however the industry never stabilized until the 1950's. Hence, one wouldn't want to choose a year from this period for the sample.

Between 1964 and 1981 Topps had a near monopoly on the card market and could control the quantity of cards brought to market. In principle, choosing a year in this interval provides a near vertical supply curve with variation between players. Until 197 3 Topps issued their cards in series each year, causing s shift of the supply curve within a year. In any given year the later series had smaller press runs. Also, fan enthusiasm tends to fade later in the season resulting in a shift of the demand curve w ithin the season. The combined factors can have an uncertain impact on card prices for a given player. In this section we have chosen 1974 as the sample year, with 660 cards issued, to avoid the issue of new entrants into the card market and the multiple series issue.

Baseball cards have their greatest value when they are part of a complete set for a given year. An entire set may be comprised of as many as 900 cards. This feature of the market establishes a lower limit on the price of a card. The lower limit is know n as the common card price. When cards are issued in series throughout the season, the common card price will change with the series. Also, the common card price adds a distortion to the way in which the market values journeyman players, lesser stars, and truly noteworthy players. Only the cards for a small number of stars are traded at a premium above the common card price. For example, a player may have 2,000 life time hits while another player may have had 15 hits in a short career, yet both cards are traded at the common card price.

The consequence of the common card price is that the distribution of card prices is censored, at $.30 for our sample year. In an empirical model with a censored dependent variable, like price, OLS is an inappropriate method of estimation. The censoring problem can be solved using two approaches. In the first approach the model parameters are estimated by the Tobit method, in which the dependent variable distribution is a mixture of discrete and continuous parts.

In the second approach, card price is treated as a latent variable. If the unobserved variable takes a value below a certain threshold, then the dependent variable is assigned a value of zero. If the unobserved dependent variable is above the threshold then the dependent variable is assigned a value of one. The model parameters are estimated by the Probit method, in which the latent variable is assumed to have a normal distribution. The second approach is attractive because the censoring of the distrib ution of card prices is rather extreme. In the usual case it is observations in one tail which are censored. In this case we observe a small number of extreme cases in one tail and the rest of the distribution has been censored.

To demonstrate the importance of the choice of sample year we first estimated the parameters of a model specified by Nardinelli and Simon (N&S, 1990). For hitters the model was

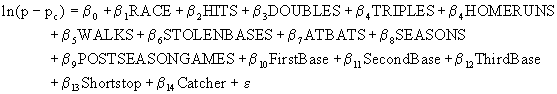
The specification includes information about the player's offensive skills, HITS etc., and defensive position, FirstBase etc., for the glamour positions. On the basis of the 1989 prices of the 1970 card set, N&S concluded " Our results indicate that consumer discrimination exists in the market for baseball cards. Among hitters, the cards of non-whites sell for about 10 percent less than the cards of white players of comparable ability... " Their conclusion applies to both th e Tobit and Probit approaches, although the result seems to be driven by discrimination against hispanic players.

Based on our 1974 sample, the results of which are presented in Table 1, we find support for their conclusion only in the Tobit results. To the extent that there is discrimination by consumers, it seems to be born by hispanic players. However, they mak e up only 5% of the sample and the result may be driven by outliers. The Probit results do not support the N&S conclusion.

The N&S specification for pitchers was

With regard to their 1970 sample, N&S wrote "The effect of being nonwhite on the card price of pitchers was somewhat greater than for hitters (13 percent versus 10 percent)." We also fit this specification to the 1974 data. The results are presented in Table 2. There is no support for discrimination by baseball card collectors in 1974 in either the Tobit or the Probit model.

Thinking that model specification may have produced the different results between 1970 and 1974, we estimated revised models for hitters and pitchers. Among offensive players, HITS, DOUBLES, TRIPLES and HOMERUNS are highly correlated, the revised m odel includes only HITS and HOMERUNS. A further reason for dropping DOUBLES and TRIPLES is that it is total hits (3,000) and home runs (500) which get a player into the Hall of Fame. We included runs batted in as a measure of whether a player's productivi ty benefited the team, or just his own statistics.

Walks is not a statistic for which players are known, so it was dropped. ATBATS is a measure of longevity, already captured by SEASONS, so it was dropped.

Participation in a post-season game does not per se convey star status. Rather, it is a player's performance in those games, so our model uses post-season home runs. One player in the sample, Reggie Jackson, even got his nickname, Mr. October, for his home runs in the playoffs.

As for defensive play, rather than use field position dummies, we have used a variable for 'Golden Gloves' won. This is an easily recognized achievement and is independent of position played. Also, it is arguable that all of the infield positions are g lamour positions; it is the player that makes the position, rather than the position which makes the player.

We have also included dummy variables for election to the Hall of Fame and being chosen Most Valuable Player. The Hall of Fame variable denotes recognition by journalists of a player's achievements subsequent to his retirement. Baseball and trading car d fans await the election results each year.

Most Valuable Player status can also give a lift to a player's card price. For example, Eddie Murray had much better performance statistics than Cal Ripken, but in 1992 the cards traded at comparable prices, due possible to Ripken's MVP awards.

There is a card vintage effect which is neglected by other studies. On average there is nearly a 80% drop in price between a player's first card to his second. An extreme example is Mickey Mantle. His 1952 Topps card has traded at $20,000 in the same y ear that his 1953 card traded for only $2,000. Hence our year variable indicates the number of annual cards issued for a player by 1974.

The results for our revised hitters specification are in table 3. There is not consumer discrimination based upon player race for the 1974 card year in either the Tobit or Probit models. HITS is significant and has the expected sign. Winning a Golden G love, being selected an MVP, and hitting more home runs during the post season all increase the price of a player's card. The other variables were not significant.

The pitcher specification used by N&S was also modified by us. Rather than total earned runs, fans are more likely to be aware of the pitcher's earned run average. Like the venerable bases on balls (walks), completed games is not relevant to modern fans, so they were dropped from the model. Hall of Fame membership was included to reflect the acclaim in which a player is held. The pitcher's equivalent of the MVP award, the Cy Young Award, was also included in our specification. A variable for Golden Gloves was included.

The results for our pitchers specification are presented in table 4. Importantly, we find no evidence of consumer discrimination in the market for baseball trading cards. Saves, post season innings pitched, and election to the Hall of Fame all were sig nificant and had the expected signs. The other variables were not statistically significant.

In a simple model of the production of baseball entertainment we have demonstrated that it is not observationally possible to use player salaries to measure employer discrimination in professional sports. In an e qually simple model of the market for baseball trading cards we have demonstrated that it is impossible to state as unequivocally as Nardinelli and Simon that "... the link between consumer racial attitudes and the price of baseball cards is direct. There is no room for owner or coworker discrimination."

Unlike Nardinelli and Simon's findings for the 1989 prices of the 1970 card set, we find there is no evidence of consumer discrimination in the 1989 prices of the 1974 baseball card set. Since the conclusion is the same for different specifications for the 1974 card set, we attribute this to the structural change in the card market in 1973. Namely, cards were no longer issued in series throughout the season after that date.

BIBLIOGRAPHY

Andersen, Torben amd Sumner J. LaCroix, 1991, "Customer Racial Discrimination in Major League Baseball", Economic Inquiry, Vol. 29, No. 4, October, Pps. 665-677.

Arrow, Kenneth J., 1972, "Models of Job Discrimination" Anthony H.Pascal, ed., Racial Discrimination in Economic Life (Lexington, MA: Lexington Books) Pp. 83-102.

Beckett, James, Official 1989 Price Guide to Baseball Cards (New York, N.Y.: The House of Collectibles).

The Baseball Encyclopedia, 1990 and 1992, Ninth and Eleventh Editions, (New York: Macmillan).

Becker, Gary, 1971, The Economics of Discrimination (Chicago, IL: Univeristy of Chicago Press).

Findlay, David W. and Clifford E. Reid, 1997, "Voting Behavior, Discrimination and the National Baseball Hall of Fame," Economic Inquiry, Vol. 35, No. 3, July, Pps. 562-578.

Gabriel, Paul E., Curtis Johnson and Timothy J. Stanton, 1995, "An Examination of Customer Racial Discrimination in the Market for Baseball Memorabilia", Journal of Business, Vol. 68, No. 2, Pps. 215-230.

Hill, James R. and William Spellman, 1984, "Pay Discrimination in Baseball: Data from the Seventies", Industrial Relations, Vol. 23, Pp. 103-112.

Kahn, Lawrence M. and Peter D. Sherer, 1988, "Racial Differences in Professional Basketball Players' Compensation," Journal of Labor Economics, Vol. 6, Pp. 40-61.

Kahn, Lawrence M., 1991, "Discrimination in Professional Sports: A Survey of the Literature", Industrial and Labor Relations Review, Vol. 44, No. 3, April, Pps. 395-418.

Lindsay, Cotton and Michael Maloney, 1988, "A Model and Some Evidence Concerning the Influence of Discrimination on Wages", Economic Inquiry, Vol. 26, Pp. 645-660.

Nardinelli, Clark and Curtis Simon, 1990, "Customer Racial Discrimination in the Market for Memorabilia: The Case of Baseball", Quarterly Journal of Economics, Vol. 105, No. 3, August, Pps. 575-595.

Scully, Gerald W., 1974, "The Economics of Discrimination in Professional Sports: The Case of Baseball," R.G. Noll, ed., Government and the Sports Business (Washington, D.C.: Brookings Institution).

Spence, Michael D., 1973, "Job Market Signalling", Quarterly Journal of Economics, Vol. 87, Pp. 355-74.