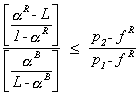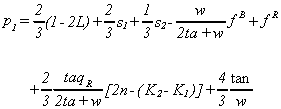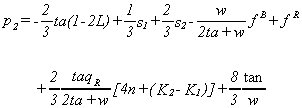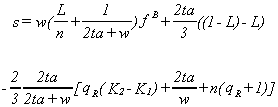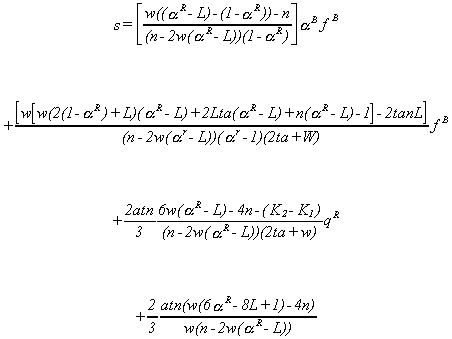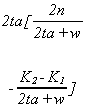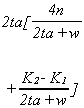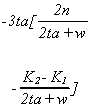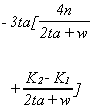Hospital Care for the Indigent:
Tradeable Admissions Permits
by
Andrew J. Buck
Temple University
and
Min Peng
University of Illinois - Chicago
JEL Classification Codes: I11, I18, D43
February 9, 1997
Hospital Care for the Indigent:
Tradeable Admissions Permits
by
Andrew J. Buck
Temple University
and
Min Peng
University of Illinois - Chicago
Abstract
The social liability of providing hospital care for the indigent is not
shared equally by all hospitals. This could lead to some socially undesirable
consequences, such as the closure of hospitals in poor areas. This paper proposes
tradeable admissions permits as a method for restoring the 'missing market' for care for
the poor. As an alternative to the prospective payments system, admissions permits can
achieve both efficiency and equity.
Hospital Care for the Indigent:
Tradeable Admissions Permits
by
Andrew J. Buck and Min Peng
1. Introduction
In the past the U.S. had locally centralized systems for dealing with the social
liability of equal access to medical care without regard to the ability to pay (Barr 1993,
Pps. 291-2 and Blaisdell 1994). The financial exigency resulting from more recenthealth
care changes has closed many voluntary and public facilities. The closure of facilities
may not be socially desirable in terms of both equity and efficiency: The burden of caring
for the medically indigent is not completely subsidized under the current and proposed
prospective payment system (PPS). Given the relative immobility of the poor, the need to
go to a hospital outside of their neighborhood may limit their access to basic care. We
propose a market for tradeable admissions permits to replace the current prospective
payment system.
The PPS was meant to promote the efficient use of resources in much the same way as price
cap regulation in highly concentrated industries, such as cable TV and telephony. Although
the PPS may have induced hospitals to operate at lower cost (Russell (1989) and Dranove
and White (1994)), it overlooks a few basic facts about health care. First, once they
become ill, the poor and elderly are more costly to treat than the affluent (Smith and
Telles 1991, Elliot, Renier and Vecchi 1995, Hahn and Flood 1995). Second, some hospitals
face a greater burden of caring for the poor than others (Sloan, Valvona and Mullner,
1986). Third, government has been greatly burdened by the prospective payments system.
Finally, the PPS is slow to adapt to changing health care practices (Myers, 1986). These
forces, on top of unilaterally determined fee schedules, all come together to place a
burden on providers and the poor. Since the PPS rates are a 'take it or leave it'
proposition the poor may find themselves without care as providers close entirely or by
stages.
In this paper we propose a system of tradeable admissions permits which obviates the need
for a government agency to worry about either the revenue or cost aspects of serving the
poor. Creating a market for the care for the poor also makes the question of a hospital's
obligation to provide care and an indigent person's right to care moot (Reinhardt 1986 and
Olick 1994). A market for permits will also be more responsive to the growing proportion
of medically indigent in the population (Sloan, Morrisey and Valvona, 1988). Also, by
using tradeable admissions permits, the public policy authority responsible for acute
health care is able to overcome the fact that neither hospitals nor patients are very
mobile.
In section 2 we state the model and prove that a market will exist for tradeable
admissions permits. Some comparative statics results are stated in section 3. Conclusions
and directions for future work are presented in section 4.
2. A Model of Tradeable Admissions Permits
There is a city arranged along a street of unit length. There are two classes of
consumers: Those who are able-to-pay for their hospital care (the rich, denoted by R) and
those who cannot (the badly off, denoted by B). The poor live on the interval [0,L]. The
rich live on the interval [L,1]. The abilities to pay of the two types of consumer are
perfectly distinguishable. The density of residents, w, along the street is the same for
both classes of consumer. Hence, the total number of poor people on the street is 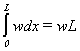 and the total number of able-to-pay people is
and the total number of able-to-pay people is 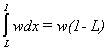 .
.
There are two hospitals in the city. Their locations are assumed to have been
predetermined by historical accident. For simplicity the hospitals are symmetrically
located about the midpoint on the street. Hospital 1, located in the poor neighborhood, is
located at ½ - a and Hospital 2, which is located in the affluent neighborhood, is
located at ½ + a. The two hospitals provide identical services and compete on the basis
of price as the strategic variable. Neither hospital can turn away a customer on the basis
of the ability to pay. This linear city and its hospitals appears as in Figure 1.
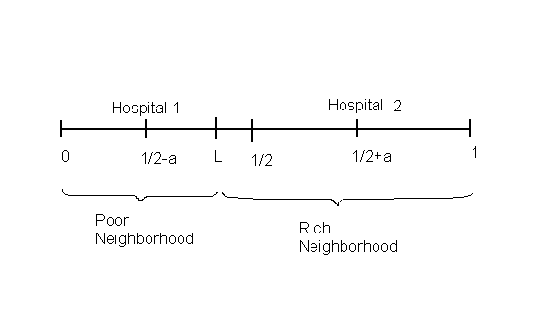
Figure 1
The consumers must make a mutually exclusive choice of hospital on the basis of
utility surplus (Anderson, DePalma and Thisse, 1992). The utility derived from choosing
hospital i=1,2 by a patient of type k=B,R who is located at x is defined by
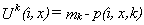 where mk is the reservation
price of patient type k for health care and p(.) is the real utility cost suffered by the
consumer upon choosing hospital i.
where mk is the reservation
price of patient type k for health care and p(.) is the real utility cost suffered by the
consumer upon choosing hospital i.
To make things specific, define the real utility cost for the able-to-pay to be
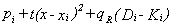 1
1
where pi is the price for a unit of care at Hospital i and t is travel cost,
assumed to be the same for both types of consumer. qj j=R,B is the opportunity cost of time for a given type
of consumer. The difference between total demand for care at the hospital, Di, and its capacity, Ki, is a measure of the waiting time for care at the ith hospital. Hence, the first term is the fee
paid by the patient or her insurance carrier, the second term is the total travel cost,
and the last term is the monetary cost of hospital congestion. Since the poor are unable
to pay any out of pocket expenses beyond transportation and the opportunity cost of
waiting, their real utility cost will be
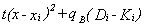 (2)
(2)
Obviously there are marginal individuals of both types who will be indifferent
between the two hospitals. The location of the marginal able-to-pay customer is found by
setting equal the utility cost of being served at the respective hospitals and solving for
x, the consumer's location. Hence, the location of the marginal able-to-pay customer is
given by
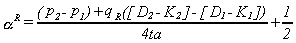 (3)
(3)
Since patients are uniformly distributed throughout the city, 1/2 is the location
of the randomly drawn patient and 4ta is that patient's cost of making a round trip to
each hospital. The numerator of the first term is the incremental monetary expense of
choosing hospital 2 instead of hospital 1. The aggregate demand of type R customers for
services at Hospital 1, located in the poor neighborhood, will be
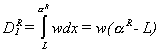 (4)
(4)
Their demand for services from Hospital 2, located in their own neighborhood, will
be 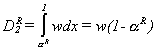 (5)
(5)
Similar calculations can be made for the unable-to-pay group of customers. The
location of the indigent patient indifferent between the two hospitals is 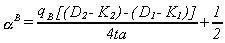
The aggregate demand of type B customers for services at Hospital 1, located in
their own neighborhood, will be 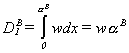 The
aggregate demand by indigent patients for services from the hospital in the affluent
neighborhood will be
The
aggregate demand by indigent patients for services from the hospital in the affluent
neighborhood will be 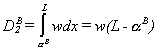
The demand side of the model can be solved to determine the number of patients
served at the poor hospital, denoted D1,
and the number served at the rich hospital, denoted D2.
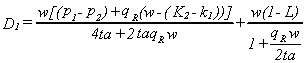 (9)
(9)
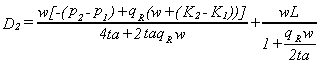 (10)
(10)
where qB has been set to one
to simplify the algebra. Turning to the supply side of the market, the constant marginal
cost of serving an able to pay customer is fR.
The constant marginal cost of serving an indigent patient is fB. In order to serve a paying customer the hospital must
have an admissions permit. Initially Hospital 1 has an endowment of n such permits. If
Hospital 1 has fewer than n paying customers then it can sell the additional permits in
the marketplace. Symmetrically, if Hospital 2 is to serve any able-to-pay customers then
it must purchase an admissions permit from Hospital 1. Formally, the objective of the
first hospital, in the indigent area, is 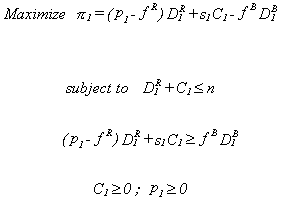 (11)
(11)
The first constraint is the sale limit constraint. A total of D1R
paying customers come to the poor hospital and it can sell an additional C1 permits at an asking price of s1 dollars each, up to the total of its initial
endowment of such permits, n. The second constraint is the incentive constraint. Hospital
1 should at least break even on the sale of patient care and admissions permits. The
objective of the second hospital, in the rich area, is similarly represented in equation
12. 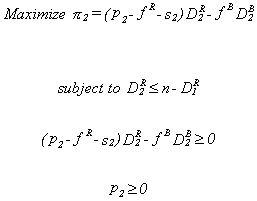 (12)
(12)
The first constraint simply states that the second hospital must purchase from
Hospital 1 a permit for every able-to-pay customer it serves. In the second constraint
Hospital 2 stipulates that it will not bid so high for a permit, s2, that it will lose money on its newly purchased permit.
Of immediate interest is whether there is a price, s, for an admissions permit which will
allow trade between the hospitals. There are both necessary and sufficient conditions. If
trade in permits is observed to have taken place then it must have been the case that
Hospital 1 was not able to cover the cost of caring for the indigent from the revenues it
earned from services sold to the affluent. That is, 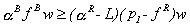 . Similarly, after paying the explicit costs of caring for both its rich and
poor patients, Hospital 2 must have some revenue left to buy permits. That is,
. Similarly, after paying the explicit costs of caring for both its rich and
poor patients, Hospital 2 must have some revenue left to buy permits. That is, 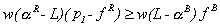 . These inequalities can be rearranged to yield
the necessary condition
. These inequalities can be rearranged to yield
the necessary condition
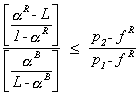
In the numerator on the left hand side is the odds of a rich patient going to
Hospital 1, the denominator is the odds of a poor patient going to Hospital 1. The right
hand side is the ratio of the Hospital 2's profit from caring for the affluent to that of
Hospital 1. Since 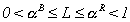 , we know that the odds
ratio and, hence the ratio of profits, will always be positive. A sufficient condition is
that at the market clearing prices for care, the difference between the bid and offer
price of a permit must be positive. Hospital 1, in the poor area, will accept a price for
its admissions permits no lower than
, we know that the odds
ratio and, hence the ratio of profits, will always be positive. A sufficient condition is
that at the market clearing prices for care, the difference between the bid and offer
price of a permit must be positive. Hospital 1, in the poor area, will accept a price for
its admissions permits no lower than 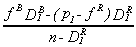 .
This is positive and finite only if the hospital can cover the care it provides the poor
with the revenue it earns from serving the able-to-pay and selling its excess admissions
permits. At the same time, the permit price must be below
.
This is positive and finite only if the hospital can cover the care it provides the poor
with the revenue it earns from serving the able-to-pay and selling its excess admissions
permits. At the same time, the permit price must be below 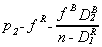 , or Hospital 2 will not buy any permits offered to it. Taking the
difference between the maximum price that Hospital 2 will pay and the minimum acceptable
price to Hospital 1 yields
, or Hospital 2 will not buy any permits offered to it. Taking the
difference between the maximum price that Hospital 2 will pay and the minimum acceptable
price to Hospital 1 yields 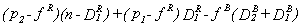 This will be
positive as long as the marginal cost of caring for the poor, fB, is not too great and/or there are not too many of them,
D2B+D1B. The maximization problem for the two hospitals
can be solved to yield the optimal prices to be charged to paying customers. The solution
will yield a Nash (price) equilibrium. The solution is found by substituting for D1R,
D1B, D2R, D2B and the aggregate demands in the objective
functions. Each hospital takes the other's price as given, so the objective functions are
differentiated with respect to the respective prices. The two first order conditions
This will be
positive as long as the marginal cost of caring for the poor, fB, is not too great and/or there are not too many of them,
D2B+D1B. The maximization problem for the two hospitals
can be solved to yield the optimal prices to be charged to paying customers. The solution
will yield a Nash (price) equilibrium. The solution is found by substituting for D1R,
D1B, D2R, D2B and the aggregate demands in the objective
functions. Each hospital takes the other's price as given, so the objective functions are
differentiated with respect to the respective prices. The two first order conditions
can then be solved for the optimal prices, given by 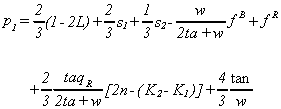
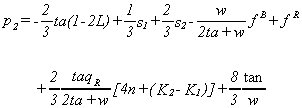
where s1 and s2 are the offer and bid prices for admissions
permits. With the prices for care in hand it is possible to re-examine the question of the
price of an admissions permit, s. This is accomplished by imposing a zero profit
constraint under a given allocation of patients between the two hospitals. From each of
the zero profit constraints one obtains an expression for the price of a permit. Setting
these prices equal to each other and substituting away from the price of care yields the
desired solution. There are four possible allocations of patients between the hospitals.
In the simplest case all of the poor patients go to Hospital 1 and all of the paying
patients go to Hospital 2. In this case the marginal patients are located at L. In the
second case Hospital 1 gets no paying patients, but some poor patients now go to Hospital
2. In the third case all of the poor patients go to Hospital 1, but some paying patients
now also go to Hospital 1. In the final case both hospitals have both types of patients.
For the first case, in which patients patronize their neighborhood hospital, the price of
an admissions permit will be
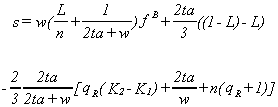
The expression is valuable for the insight offered by the individual arguments
rather than by the overall intuition. qR
is the opportunity cost of waiting for those who are able to pay. K2-K1
is the net capacity of Hospital 2 over Hospital 1. fB
is the marginal cost of caring for an additional indigent patient. Other terms offer
valuable interpretations. First note that 2ta/w is the per capita cost of a trip between
the two hospitals. L/n is the ratio of poor patients to the number of paying patients for
whom permits are available. n/w is the ratio of paying patients for whom there are permits
to the number of patients in the population. (1-L)-L is the net proportion of paying
patients in the population. Hence, s>0 if travel costs are not too high, the
opportunity cost of waiting is not too great, the proportion of poor is low enough, and
hospital 2 has enough capacity relative to hospital 1. In the fourth, and most general,
case the price of an admissions permit is 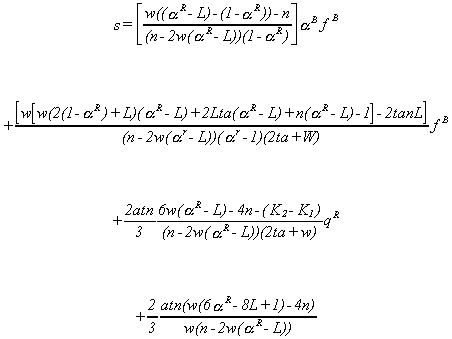
Again, the overall expression is not intuitive. However, the individual terms do
have interesting interpretations in their own right. aR-L is the proportion of paying patients who
receive service from Hospital 1 and 2ta is the cost of a trip between the hospitals. Not
surprisingly, the price of an admissions permit is an increasing function of the location
of the marginal poor patient (aB) and the marginal cost of caring for the poor. Other
comparative static results are taken up in the next section.
Implications
At the equilibrium prices, comparative statics yields some interesting results,
summarized in Table 1. The first column shows the variable being changed. The remaining
columns of the table can be divided into two parts in the vertical dimension. The first
pair of columns show the response of the price of care to changes in key variables. The
second pair of columns shows the response of the bid (s2) and offer (s1)
price of an admissions permit to changes in key variables. Changes in the price of care
are considered first. As the offer price of an admissions permit rises, Hospital 1 will
increase the price it charges those who are able to pay for care. This response is a
result of the fact that caring for the affluent now has a higher opportunity cost.
Hospital 1's response to an increase in Hospital 2's bid price for a permit is also
positive but smaller. Again the response is explained by a higher opportunity cost of
providing care rather than selling the right to provide care. The price charged for care
by a hospital increases as its own capacity increases. An increase in capacity will reduce
waiting time. In turn, the total opportunity cost incurred by a paying patient will fall.
As a consequence the hospital is able to raise price and capture some of the consumer's
net gain in the real utility cost of having purchased care. If the hospital's competitor
increases capacity then the correct response is to drop price. As the opportunity cost of
time for the affluent (qR) increases,
the price for their care will rise at both hospitals. That is, the hospitals correctly
determine that price can be used to ration capacity so that the total cost of waiting by
an affluent patient will remain unchanged. As the proportion (L) of unable-to-pay patients
in the population increases, the price for care falls at Hospital 1 and rises at Hospital
2. This results from Hospital 1 having to compete more fiercely for the dwindling number
of geographically more distant patients who are able to pay. At Hospital 2 they must raise
the price for the affluent as their burden of unable to pay patients increases. The price
response to an increase in the marginal cost of caring for the able to pay is also equal
to the opportunity cost of time for the indigent. However, if the marginal cost of caring
for an indigent patient rises then the price charged to the affluent must decrease. This
response is necessary to attract more paying customers to offset the higher cost of caring
for the indigent. Turning to the effects of variable changes on admissions permit prices,
the minus signs in admissions permit cross derivatives indicate that the spread between
the offer and bid price will increase in response to an increase in either one of them. An
increase in its own capacity will cause Hospital 1 to lower its offer price. The logic is
that reduced waiting time will draw more paying customers to Hospital 1 so the sale of an
admissions permit to Hospital 2 is not as attractive. An increase in Hospital 2's capacity
will cause Hospital 1 to raise the offer price for a permit. In this case waiting times at
Hospital 2 are falling so more paying patients will go there and the hospital is willing
to pay more for the right to care for them. The explanation of the sign patterns for
Hospital 2's bid prices is symmetric. An increase in the opportunity cost of time for the
affluent (qR) will cause both offer
and bid price for a permit to fall. Both prices fall because the total fee for service
must fall to compensate the able to pay customer for the increasing cost of waiting for
care. As the proportion of indigent in the population increases, the first hospital will
raise its offer price. This is necessary in order to offset the increased burden of caring
for the indigent. Hospital 2's burden of caring for the poor will also increase, hence
they will not pay as high a price for the right to provide care for the affluent. When the
marginal cost of caring for the indigent rises, Hospital 1 must ask a higher price for its
permits and Hospital 2 will raise the price it is willing to pay for those permits. The
response of Hospital 1 is obvious. The response of Hospital 2 is explained by the fact
that it is willing to pay more for the right to care for the affluent, the only source of
income to offset the cost of caring for the poor. When the cost of caring for the affluent
goes up, the price that Hospital 1 asks for its permits will go down and the willingness
of Hospital 2 to pay for a permit will also decline. Hospital 1 must lower its offer price
and Hospital 2 must lower its bid price since a paying customer is no longer as lucrative.
4. Conclusions In this paper we have
modeled the essential features of the urban healthcare landscape. Namely, as a result of
historical accident some hospitals are located in poor areas and have an excessive burden
of caring for the poor. Other hospitals located in more affluent neighborhoods do not have
a comparable burden. The result is that although the hospitals in the two types of
neighborhoods may be equally well run, one group is always on the brink of financial ruin.
To overcome the unequal burden, society has relied on various public care arrangements and
inserted uncompensated care components into the prospective payment systems. Medicaid is
used to reimburse for care provided to the poor and uninsured. Medicare is used to provide
for the underinsured elderly. The reimbursement schedules are determined unilaterally by
large, slow moving bureaucracies which are only moderately responsive to the vicissitudes
of the market place. A recently proposed solution is to tax insurance carriers in order to
finance the care for the indigent. Neither Medicare/Medicaid nor a system of taxes will be
successful since neither mechanism solves the problem of the missing market for the care
of the medically indigent. In the model proposed here the hospitals located in poor
neighborhoods are endowed with the right to care for patients who are able to pay, either
out of pocket or with insurance. These rights are termed admissions permits. Hospitals in
affluent neighborhoods must purchase the right to care for patients from the their less
affluent brethren. This places the mechanism for determining the appropriate reimbursement
schedule in the hands of those who need care and those who provide it. An additional
feature would be reduced courtship of paying patients (Braithwaite 1993). Permit prices
would reflect case load mix, the proportion of poor in the wider urban area, and the costs
of travel and waiting for care. The model can be modified to illustrate and compare the
welfare effects of health care markets which do not have permit trading with those that
allow permit trading and with those in which the hospital receives a lump sum subsidy for
each patient treated. The model could also be used to explore the incentives for an
affluent hospital to operate an outpatient clinic in the shadow of the poor hospital. By
providing such care, the affluent hospital reduces the marginal cost of caring for the
indigent at the poor hospital. As a result, the price of a bed permit would decline.
Table 1
Comparative Statics:
Impact of Parameter Changes
|
|
Price of Care
|
Price of Permit
|
Variable
|
Hospital 1
|
Hospital 2
|
Hospital 1's Offer Price
|
Hospital 2's
Bid Price
|
S1
|
2/3
|
1/3
|
- -
|
-2
|
S2
|
1/3
|
2/3
|
-1/2
|
- -
|
K1
|
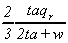
|
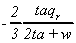
|
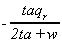
|
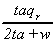
|
K2
|
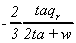
|
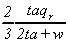
|
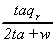
|
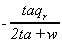
|
qr
|
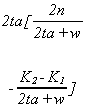
|
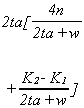
|
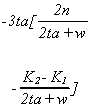
|
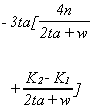
|
L
|
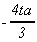
|
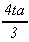
|
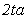
|
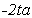
|
fB
|
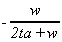
|
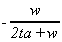
|
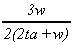
|
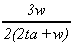
|
fR
|
1
|
1
|
-3/2
|
-3/2
|
Bibliography
Anderson, Simon P., Andre dePalma and Jacques-Francois Thisse, 1992, Discrete Choice
Theory of Product Differentiation, (MIT Press, Cambridge).
Barondess, Jeremiah A., 1993, "Municipal Hospitals in NY: A Review of the Report
of the Commission to Review the Health and Hospitlas Corporation", Bulletin of the
New York Academy of Medicine, Vol 70, No. 1, Summer, Pps. 8-25.
Barr, Nicholas, 1993, The Economics of the Welfare State, (Weiden and Nicholson,
London).
Belzer, Michael D., 1995, "Will Congress Shred the Safety Net?", Postgraduate
Medicine, Vol, 98, No. 12, December, P. 15.
Blaisdell, F.W., 1994, "Development of the City-County (Public) Hospital", Archives
of Surgery, Vol. 129, No. 7, July, Pps. 760-764.
Blankenau, R., 1993, "Caring for the Poor - and More", Hospitals,
Vol. 67, No. 4, Pps 42, 44.
Blumstein, James F., 1986, "Providing Hospital Care to Indigent Patients:
Hill-Burton as a Case Study and a Paradigm", in Uncompensated Hospital Care:
Rights and Responsibilities, Frank A. Sloan, James F. Blumstein and James M. Perrin
(eds.), The Johns Hopkins University Press, Pps. 94-107.
Braithwaite, S.S., 1993, "The Courtship of the Paying Patient", Journal
of Clinical Ethics, Vol. 4, No. 2, Summer, Pps. 124-133.
Carvajal, Doreen, 1995, "Vying for Patients, Hospitals Think Location,
Location", The New York Times, January 22, Pps. 25-26.
Cantor, Joel C., 1993, "Health Care Unreform: The New Jersey Approach", Journal
of the American Medical Association, Vol. 270, No. 4, December, Pps. 2968-2970.
Dranove, David and William D. White, 1994, "Recent Theory and Evidence On
Competition in Hospital Markets", Journal of Economics and Management Strategy,
Vol. 3, No. 1, Pps. 169-209.
Elliot, B., C. Renier, and L. Vecchi, 1995, "Health Care for the Uninsured in
Duluth", Minnesota Medicine, Vol. 78, No. 3, pps. 25-29.
Frank, Richard G. and David S. Salkever, 1991, The Supply of Charity Services by
Nonprofit Hospitals: Motives and Market Structure, RAND Journal of Economics 22,
430-445.
Fritsch, Jane, 1995, State Regulators Review New York City's Public Hospitals, New
York Times, March 8, B1.
Hahn, B. and A.B. Flood, 1995, "No Insurance, Public Insurance, and Private
Insurance: Do These Options Contribute to Differences in General Health?", Journal
of Health Care for the Poor and Underserved, Vol. 6, No. 1, Pps. 41-59.
Mallenby, M.L., 1993, "Health Care for Nebraska's Medically Indigent", Journal
of Health Care for the Poor and Underserved, Vol. 4, No. 3, pps. 177-93.
Milgrom, Paul, 1992, "Auctions and Bidding: A Primer", Journal of
Economic Perspectives, Vol. 3, No. 3, Pps. 3-22.
Myers, Beverly A., 1986, "Public Subsidies for Hospital Care of the Poor:
Medicaid and Other Myths of Equity", in Uncompensated Hospital Care: Rights and
Responsibilities, Frank A. Sloan, James F. Blumstein and James M. Perrin (eds.), The
Johns Hopkins University Press, Pps. 16-53.
Myerson, Roger B. and Mark A. Satterthwaite, 1983, "Efficient Mechanisms for
Bilateral Trade", Journal of Economic Theory, Vol. 29, No. 2, Pps. 265-281.
Olick, R.C., 1994, "Health Care Reform and the Right to Health Care", New
Jersey Medicine, Vol. 91, No. 7, July, Pps. 472-476.
Reinhardt, Uwe, 1986, "Uncompensated Hospital Care", in Uncompensated
Hospital Care: Rights and Responsibilities, Frank A. Sloan, James F. Blumstein and
James M. Perrin (eds.), The Johns Hopkins University Press, Pps. 16-53.
Russell, Louise B., 1989, Medicare's New Hospital Payment System: Is It Working?, (The
Brookings Institution, Washington, D.C.). Sloan, Frank A., James F. Blumstein and James M.
Perrin (eds.), 1986, Uncompensated Hospital Care: Rights and Responsibilities, The Johns
Hopkins University Press, Baltimore, Pps. 16-53.
Sloan, Frank A., Joseph Valvona and Ross Mullner, 1986, "Identifying the Issues:
A Statistical Profile", in Uncompensated Hospital Care: Rights and
Responsibilities, Frank A. Sloan, James F. Blumstein and James M. Perrin (eds.), The
Johns Hopkins University Press, Pps. 16-53.
Sloan, Frank A., Michael A. Morrisey and Joseph Valvona, 1988, "Hospital Care for
the "Self-Pay" Patient", Journal of Health Politics, Policy and Law,
Vol. 13, No. 1, Spring, Pps. 83-102.
Smith, David B. and Joel L. Telles, 1991, A Population Based Analysis of the Effect of
Disproportionate Share on Patterns of Hospital Care in a Metropolitan Area, (Delaware
Valley Health Education and Research Foundation, Philadelphia).
Weiner, Saul J., 1992, "Bad Debt and Medical Indigence in Primary Care", Journal
of Family Practice, Vol. 34, No. 4, April, Pps. 407-408.
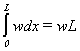 and the total number of able-to-pay people is
and the total number of able-to-pay people is 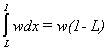 .
.
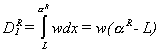 (4)
(4) 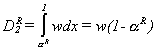 (5)
(5) 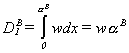 The
aggregate demand by indigent patients for services from the hospital in the affluent
neighborhood will be
The
aggregate demand by indigent patients for services from the hospital in the affluent
neighborhood will be 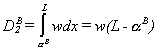
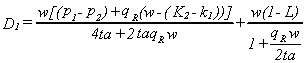 (9)
(9) 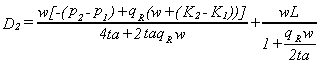 (10)
(10) 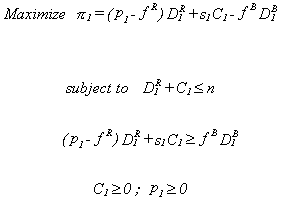 (11)
(11)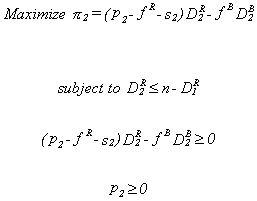 (12)
(12)