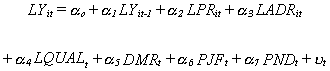Temple University
Department of Economics

Economics 616
Econometrics II

Random and Fixed Effects Models

There are three data sets for this exercise: QUAL1.TXT, QUAL2.TXT and QUAL3.TXT. The original exercise can be found in Berndt's The Practice of Econometrics: Classic and Contemporary, Addison Wesley. Each of the data sets has fifty four bimonthly observations for the period September/October 1973 through July/August 1982 for five regions of Canada. The variables included in each file are

QUAL1.TXT
OBSNO - - Observation number
LQUAL - - A measure of advertising quality
LY1, LY2, LY3, LY4, LY5 - - the log of sales in 1971 dollars for each of the five regions
DMR - - a dummy variable for product change
PJF - - a dummy variable for January/February
PND - - a dummy variable for November/December

QUAL2.TXT
OBSN - - Observation number
LPR1, LPR2, LPR3, LPR4, LPR5 - - log of a deflated regional price index for each of the five regions.

QUAL3.TXT
OBSN - - Observation number
LADR1, LADR2, LADR3, LADR4, LADR5 - - log of an index for advertising for each of the five regions in constant dollars

1. Plot the data series for LYj, LPRj, LADRj (j=1,...,5) and LQUAL with the OBSN on the horizontal axis. Is there much variation within regions over time? Is there much variation between regions at a point in time?

2. Using OLS, estimate the coefficients of

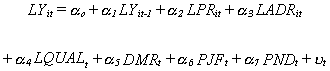
1

• for each of the i=1,...,5 regions. What are the short run advertising elasticities? Are they different from zero, statistically? What are the long run advertising elasticities? Are they different from zero? Since the long run elasticities are nonlinear functions of random variables you will have to read your text in order to find out the variance of a nonlinear combination.
  
  3. For each region, allow for first order autocorrelation and reestimate the parameters of the model. Is the autocorrelation statistically significant? How have your results changed?
  
  4. Now estimate the model under the restriction that while the intercepts differ between regions, the slope coefficients do not. This is a fixed effects model. In this least squares dummy variable model, do not correct for autocorrelation. Construct a test of hypothesis that the intercepts are different across regions. Separately test the hypothesis that the slope coefficinets are equal across regions.
  
  5. Estimate the parameters of a model in which the between regions effect is random. The slope coefficients are constant across regions in this model. Do the slope coefficient estimates differ from earlier findings?
  
  6. Execute a statistical test to choose between the fixed effects and the random effects model.
  
  7. Apart from the large number of coefficients to be estimated, why would time dummies be impractical for the model being analyzed here?
  
  8. Finally, estimate the parameters of a model in which there are region dummies and in which autocorrelation is corrected. Of all the models you have estimated in this exercise, which do you prefer?