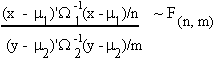
VII. REVIEW OF LINEAR ALGEBRA^*

A.1 ADDITION

Vector addition is defined component wise:

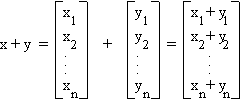
A.2 SCALAR MULTIPLICATION

Scalar multiplication is similar. x is an n component vector, a is a scalar.

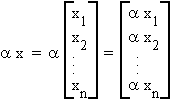
A.3 INNER PRODUCTS

Let

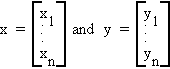
the inner product of x and y is a number

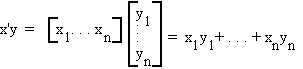
B.1 INDEPENDENCE OF VECTORS

Consider the following set of n-dimensional vectors

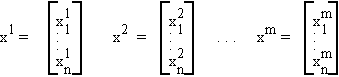
written more compactly as {x¹, x², . . . , x^m}.

The set of m vectors is said to be independent if no one of them can be written as a linear combination of the others. If {x¹,x²,…,x^m} are independent then there exists no set of non-zero scalars {a₁, a₂, . . . ,a_m} such that

B.2 ORTHOGONALITY

Two vectors x and y are orthogonal if and only if

This implies x ^ y or if q is the angle between them, then cosq = 0.

B.3 BASIS OF A VECTOR SPACE

A set of vectors {x¹,…,x^m} which are independent span the vector space V of dimension m.

For example, let m = 3

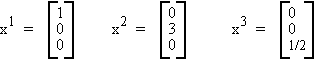
These three vectors can be used to construct any vector in R³.

Any M dimensional vector in V can be constructed as a linear combination of the vectors x¹,x²,…x^m if those vectors are independent.

A set of m vectors which span a space V of dimension m are said to form a basis for that space.

Theorem:

Every subspace has a basis. If {a1, ... , ak} and {b1, ... , bk} are two alternative bases then h = k.

Theorem:

Every vector in a subspace m has a unique representation in terms of a given basis.

Proof:

{a1, ... , ak} is a basis for m. Let x = Saiai = Sbiai Þ S(ai - bi)ai = 0 and since the ai are linearly independent we know ai - bi = 0 " i.

B.4 NORMS

The length or norm of a vector x is defined as

Two vectors x,y are said to be orthonormal if and only if

1. ||x|| = ||y|| = 1

2. x'y = 0

Example:

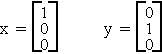
D.1 MATRIX ADDITION

Let

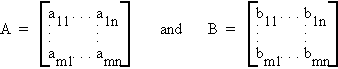
then

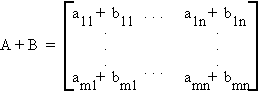
So matrix addition is defined component wise. Note that A and B must be of the same dimension. They are said to be conformable for addition.

Properties:

Let A = [aij]mxn, B = [bij]mxn, C = [cij]mxn, a, b scalars.

1. A = B iff aij = bij " i, j

2. C = A ± B iff cij = aij ± bij " i, j

3. aA = [aaij]mxn

4. a(A + B) = aA + aB

5. aA + bA = (a + b)A

6. A ± B = B ± A (commutative law)

7. A ± (B ± C) = (A ± B) ± C (associative law)

D.2 MATRIX MULTIPLICATION

Let A be an mxn matrix and B be an nxm matrix

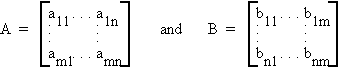
then

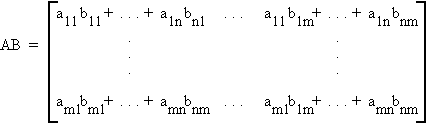
Note: 1. AB is mxm

2. The number of columns of A is equal to the number of rows of B.

Example:

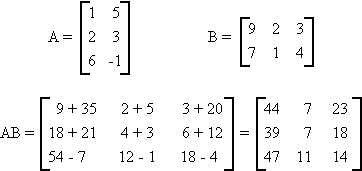
Note: Amxn and Bnxm

AB = C an mxm matrix

BA = D an nxn matrix

\ AB ¹ BA under most circumstances.

But:

1. A(B + C) = AB + AC

2. (A + B)C = AC + BC

3. AB = 0 ¹> A = 0 or B = 0

4. AB = AC ¹> B = C

D.3 DETERMINANTS

Finding the determinant of a matrix is a rule for finding a single valued representation of that matrix.

Example:

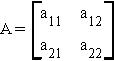
then

Example:

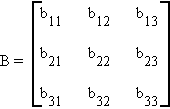
then

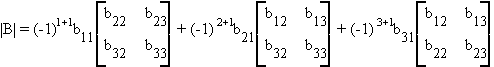
|B| = b11(b22b33 - b23b32) - b21(b12b33 - b32b13) + b31(b12b23 - b13b22)

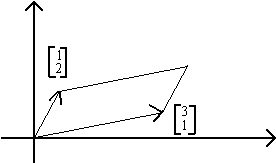
GEOMETRIC INTERPRETATION OF DETERMINANTS

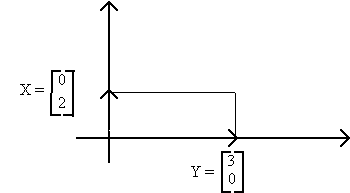
|A| is the area enclosed by the two vectors.

RULES ABOUT DETERMINANTS

1. |A| = |A'|

2. If B is obtained by exchanging a pair of rows (columns) of A then |B| = -|A|.

3. If the rows or columns of A are linearly dependent then |A| = 0 and A is said to be singular.

4. If B is obtained by multiplying one row of A by a scalar a then |B| = a|A|.

5. |AB| = |A||B|

TRANSPOSE OF A MATRIX

Let A be an mxn matrix, then the transpose of A, denoted A', is an nxm matrix, i.e., if A = [aij] then A' = [aji].

Example:

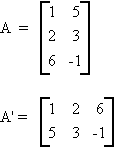
Some rules:

1. (A + B)' = A' + B'

2. (AB)' = B'A'

Let A be the mxm matrix

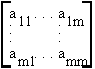
When from A the elements of its i^th row and j^th column are removed, the determinant of the remaining square matirx is called a first minor of A, denoted by Aij. The signed minor (-1)^i+j Aij is called the cofactor of aij.

D.5 RANK OF A MATRIX

Let A be an mxn matrix. The row rank of A is the largest number of linearly independent rows. If all the rows of A are linearly independent then A is said to be of full row rank. Column rank is the largest number of linearly independent columns.

Properties:

1. row rank = column rank

2. r(AB) £ r(A) and r(B)

3. r(A) + r(A') = r(AA') = r(A'A)

4. r(A + B) £ r(A) + r(B)

5. if |Amxm| = 0 then r(A) < m

D.6 SYSTEMS OF EQUATIONS

Theorem:

Consider a linear homogeneous equation Ax = 0 where A: mxn, x: nx1 unknown, 0: nx1

1. The necessary and sufficient condition for Ax = 0 to have a nontrivial solution is the r(A) < n

2. The solutions of Ax = 0 form a linear subspace

3. Let S be the subspace of solutions. Then the dimension of S is equal to n -

r(a).

Corollary:

Under the normalization rule, ||x|| = 1, the necessary and sufficient condition that Ax = 0 is that r(A) = n - 1.

Theorem:

Consider the nonhomogeneous equation

where A: mxn, b: mx1, x: nx1 (unknown) and b ¹ 0. The system has a solution iff

and has a unique solution iff

=

D.7 INVERSE OF A MATRIX

A square matrix A has at most one inverse; that is, the inverse of a matrix is unique, if it exists.

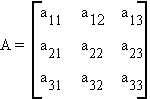
Define a cofactor as the signed determinant of the submatrix found by deleting the i^th row and j^th column of A.

Example:

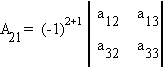
If A is non-singular, then its inverse is given by

where [Aij]' is the matrix of cofactors, transposed; the adjoint of A.

Example:

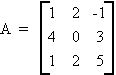
|A| = (-1)²(1)(0-6) + (-1)³(4)(10 + 2) + (-1)⁴(1)(6 - 0)

= (-6) - (48) + 6

= - 48

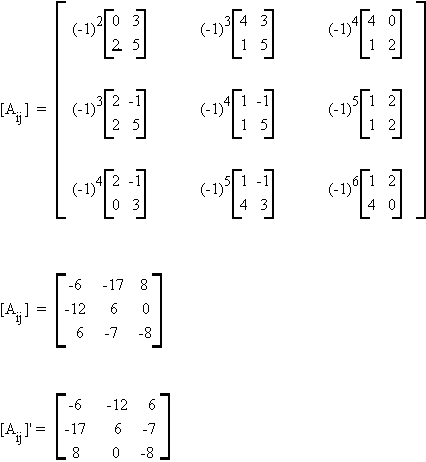
so

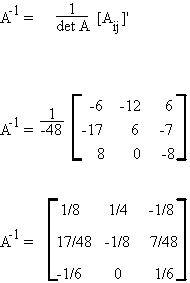
Let us see if A^-1A = I.

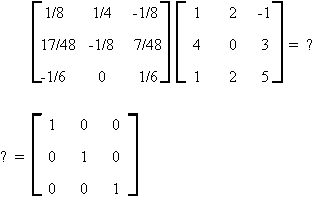
You should note the following about the matrix A

1. |A| ¹ 0

2. rows of A are linearly independent

3. columns of A are linearly independent

Some rules:

1. (AB)-1 = B-1A-1

2. the inverseof a diagonal matrix is the product of the elements.

D.8 TRACE OF A MATRIX

1. Tr A =

2. tr kA = k tr A, where k is a scalar

3. tr(AB) = tr(BA)

4. tr(In) = n

E.1 TRANSFORMATIONS

A mapping or transformation is a rule assigning a vector in Rn to a vector in Rm. The analogy is found in univariate algebra where

In matrix algebra we have

where X and Y are vectors of dimension n and m respectively and A is a matrix of dimension mxn.

For example, let

and

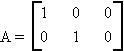
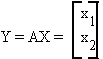
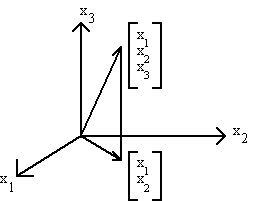
In this example, A projects the 3-dimensional vector into the two-dimensional plane.

E.2 PROJECTIONS AND IDEMPOTENT MATRICES

Any matrix A which satisfies A'A = A is said to be idempotent. Examples would be the identity matrix or:

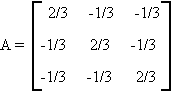
In statistical estimation we often use projection theorems unknowingly.

Consider the simple linear model

where Y is an nx1 vector, observed;

X is an nxk matrix, (n > k), fixed;

u is an nx1 random vector;

and b is a k-dimensional vector, unknown

Each column of X represents a directed line segment in en.

If the columns of X are linearly independent then they form the basis for a k-dimensional subspace of en.

Note that Y is a directed line segment in en.

Suppose we project Y onto the space spanned by the columns of X.

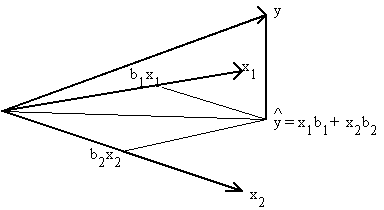
Since the xi are themselves n-dimensional, y will also be n-dimensional.

The matrix that projects Y into M(X) is

so

note that

is idempotent.

Notice also that the error of our estimate

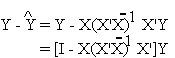
also makes use of an idempotent matrix.

An idempotent matrix is a matrix such that A = A2. For example, I - (1/n)ee'; where e is a column of ones.

Properties:

1. if A is idempotent and nonsingular then A = I

2. all idempotent maticies of less than full rank are positive semidefinite.

3. If A is idempotent of rank r then there exists an orthogonal matrix p such that

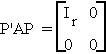
4. r(A) = tr(A) for A idempotent.

F. ELEMENTARY OPERATORS

1. Eij is an identity matrix with its i^th and j^th rows interchanged

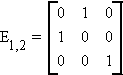
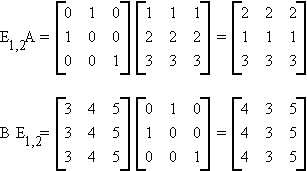
premultiplication of a matrix by Eij exchanges the i and j rows

postmultiplication by Eij exchanges the i and j columns.

2. Dr(l) replaces the r1rth element of the identity matrix by l.

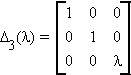
premultiplication of a matrix A by Dr(l) multiplies the rth row of A by l.

postmultiplication of A by Dr(l) multiplies the rth column of A by l.

3. Pi,j(l) places l in the i, j position of the identity matrix.

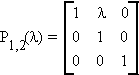
premultiplication of A by Pij(l) adds l jth row to the ith row

postmultiplication of A by Pij(l) adds l jth column to the ith column

Theorem:

For any mxm matrix A there exists a nonsingular matrix B such that BA is in echelon form.

(a) each row of BA consists of all zero or a 1 preceded by a zero

(b) any column containing the first unity of a row has as the rest of its elements zero.

Example:

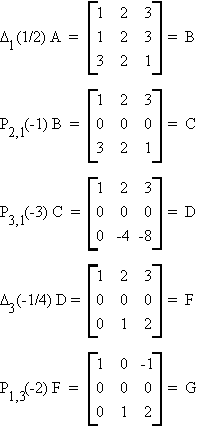
Theorem: Hermitian Canonical Form

There exists a nonsingular matrix C such that

where H is

(a) upper triangular (hij = 0, i > j)

(b) H2 = H

(c) hii = 1 or 0

(d) if hii = 1 then hji = 0 " j ¹ i

if hii = 0 then hji = 0 " j

Example:

Consider G of the previous example

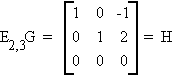
Theorem: Diagonal Reduction of a Matrix

Consider Amxn, r(A) = r. Then there exists an mxm matrix B and an nxn matrix C, both nonsingular, such that

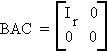
Example:

Consider H of the previous example

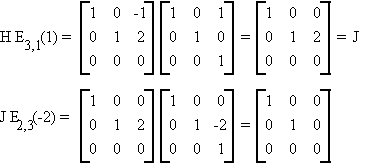
Theorem: Reduction of a Symmetric Matrix

If Amxm and A = A' then there exists a nonsingular matrix B such that

where D is a matrix that has nonzero elements only on the main diagonal. If r(a) = m then dii ¹ 0 for i = 1, 2, ... , m; if r(a) = r < m then m - r of the dii are zero. Since B is nonsingular we also have

Example:

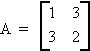
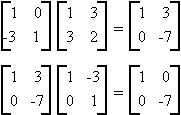
G. QUADRATIC FORMS

Let X be an n-dimensional vector and A an nxn matrix.

Then a quadratic form is

The quadratic form X'AX and the related matrix A are said to be positive definite if

and positive semidefinite if

it is negative definite if

and negative semidefinite if

Theorem:

If A is positive definite then B'AB is positive definite iff B is nonsingular or,

A: p.d Û B'AB p.d. when |B| ¹ 0

Proof: Þ

Y'B'ABY = (BY)'A(BY) > 0

Ü

X'AX = X'B'-1B'ABB-1X

= (B-1X)'B'AB(B-1X) > 0

" X ¹ 0

Theorem:

Every quadratic form can be reduced to a form containing square terms only, by a nonsingular transformation. That is, there exists a nonsingular matrix B such that

where X = BY or Y = B^-1X

Corollary:

Where r(A) = r, A: mxm

X'AX can be transformed to

where each Ui is a linear function of the elements of X.

Theorem:

If A is positive definite then there exists an upper triangular, nonsingular transformation

such that

That is

or

and T is known as the triangular square root of A.

H. CHARACTERISTIC ROOTS & VECTORS

H.1 Roots and vectors

Consider the square matrix A: nxn, a scalar l, and a vector X ¹ 0 such that

or

since X ¹ 0 it must be true that the columns of A - lI are linearly dependent, therefore

This is known as the determinantal equation.

The set of scalars that make this true are known as latent roots, eigen values, or characteristic roots.

Consider

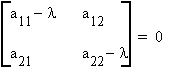
This is a quadratic equation with two solutions

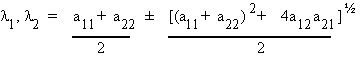
Corresponding to each unique characteristic root there is a characteristic vector so that

Let A be an arbitrary symmetric nxn matrix and C be the matrix of its characteristic vectors with

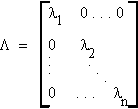
then

Theorem:

Let A = [aij]nxn. Then there exist n complex numbers l1, ... , ln that satisfy |A - lI| = 0.

Theorem:

A = [aij]nxn has at least one zero root iff A is singular.

Theorem:

Let A = [aij]nxn and C = [cij]nxn. Then the four matrices A, C-1, AC, CAC-1 all have the same set of characteristic roots.

Theorem:

A = [aij]nxn. Then A and A' have the same characteristic roots but need not have the same characteristic vectors.

Theorem:

A = [aij]nxn. If l is a characteristic root of A then 1/l is a root of A-1.

Theorem:

A = [aij]nxn and symmetric.

1. The characteristic roots of A are real and the vectors are chosen to be real.

2. Any pair of characteristic vectors are orthogonal if the corresponding roots are no equal.

3. A: p.d Þ li > 0 i = 1, ..., m

4. A: p.s.d Þ li ³ 0 i = 1, ... , m

Theorem:

If A is positive definite then there exists a nonsingular transformation such that

Theorem: Canonical Reduction of a Symmetric Matrix

A = [aij]mxm, A = A'

There exists an othogonal matrix P such that

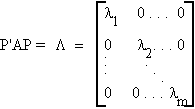
That is

A = PLP'

= l1P1P1' + ... + lmPmPm'

Theorem:

A = [aij]mxm, A = A'

B = [bij]mxm, B = B'

(i) Roots of |A - lB| = 0 are roots of T^-1AT^-1 where B = T'T

(ii) There exists a matrix R such that

Theorem:

A = [aij]mxm, A = A', p.d

(i) |A| = li

(ii) trace A = Saii = Sli

(iii) Roots of I - A are equal to 1 - li.

H.2 Extrema of Quadratic Forms

Assume

1. A: mxm symmetric

2. l1 ³ l2 ³ . . . ³ lm

3. P1, P2, ... , Pm are corresponding characteristic vectors.

Theorem:

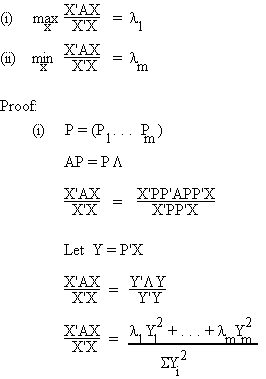
= Swili

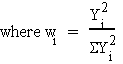
S wi = 1, wi > 0

so Swili £ l1

³ lm

Corollary:

max X'AX = l1

||X|| = 1

min X'AX = lm

||X|| = 1

Theorem:

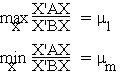
where m1 and mm are respectively the largest and smallest roots of |A - mB| = 0.

I. CALCULUS AND MATRIX NOTATION

1. Let Y = Xb be an nx1 vector where

then

2. Consider the quadratic form

Q = (Y - Xb)' (Y - Xb)

Q = Y'Y - Y'Xb - b'X'Y + b'X'Xb

Since each term is just a number we can combine the two middle terms

Q = Y'Y - 2Y'Xb + b'X'Xb

Now

differentiation is defined element wise.

J. JACOBIAN DETERMINANT

Form the matrix of n first partials for the set of n equations

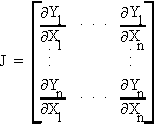
Now find the determinant of J

This is the jacobian determinant

If |J| = 0, then the equations in the original system are functionally dependent.

Hessian determinant is the determinant of the matrix of second and cross partials.

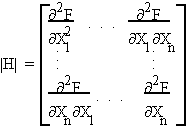
used to determine extrema.

K. PROBABILITY AND MATRIX NOTATION

1. NORMAL

Suppose Xi ~ N(m, s²) then the n-dimension vector

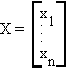
is distributed as

where m: nx1, W = s²I is nxn.

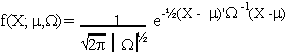
2. CHI SQUARE

(1) Let X ~ N(m, W), X: nx1, then

(x - m)'W-1(x - m) ~ c_n²

(2) Suppose Y ~ N(0, s²Inxn) and W is nxn but r(W) = n - k then

s²

3. STUDENT'S t DISTRIBUTION

Let X ~ N(m1, W1) and Y ~ N(m2, W2); X: nx1 and Y: nx1 if X and Y are independent, then

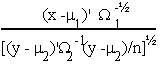
is distributed as t with n degrees of freedom.

4. F-DISTRIBUTION

If X ~ N(m1, W1) X: nx1

Y ~ N(m2, W2) Y: mx1

and then