Introduction to Game Theory

An Introduction to Game Theory

Game Theory: A formal way to analyze interaction among a group of rational agents who behave strategically.

Strategic interactions in which we can use game theory: Voting, auctions, bankruptcy, R&D races, cartel behavior, and more. In these 'game' situations we need to ask:

Who are the players?
What are the alternative strategies available to the players?
When does each player take her turn?
How much do the players stand to gain?

There are two formal representations for presenting our concept of a game:

The extensive form
The strategic form

Background:

1. The three contributions of von Neumann and Morgenstern.

2. John Nash's contribution.

3. Selten's contribution

4. Harsanyi's contribution.

A prisoner's dilemma in strategic form

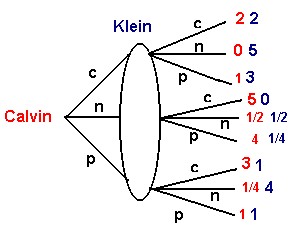
Calvin and Klein have been arrested for theft of good taste in fashion. They are being held in separate cells in the jail with no way to communicate with one another. In their interrogation they have been presented with the following table:

		Klein
		Confess	No Confession	Partly
Calvin	Confess	2, 2	0, 5	1, 3
	No Confession	5, 0	1/2, 1/2	4, 1/4
	Partly	3, 1	1/4, 4	1, 1

If they both confess to the crime then they will both go to jail for 2 years. Calvin can cut a deal: If he confesses and Klein does not, then Calvin's confession can be used to sentence Klein to five years in jail and Calvin will walk. If Calvin gives a full confession but Klein only admits complicity then Calvin gets a year and Klein is sentenced to three. The rest of the table is read the same way.

Questions to ponder about this game:

Who are the players?
When do they play?
Without knowing specifically the disutility of serving time in prison, can you rank order the player's preferences for the outcomes of the game?
If Calvin knew the probabilities with which Klein was going to play certain strategies, could Calvin calculate his own expected disutility?
What should the prisoners' strategies be? In this example the payoffs are penalties, so the players want as small a payoff as possible.

A prisoner's dilemma in extensive form

The same game can be drawn in extensive form.

Extensive.jpg (18061 bytes)

In addition to the questions of who, what and when, there are a couple of other things to think about when looking at this tree diagram:

Where is the root and where are the branches?
What is the significance of the ellipse?
What is meant by 'information set'?
How would the diagram change if the players moved sequentially?
What is a decision node?